Деревья, вероятность и генетика
Отыскание кратчайшего пути
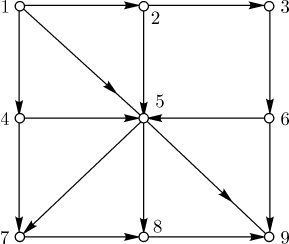
На (рис. 13.1) изображена схема местности. Передвигаться из пункта в пункт можно только по стрелкам. В каждом пункте можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из этих путей наименьшая длина? У какого наибольшая? Ответить на эти вопросы помогают деревья.
Начиная с вершины 1, последовательно "расслаиваем" граф путей в дерево. При этом каждая вершина столько раз получает самостоятельное значение, сколько в нее в первоначальном графе входило путей (рис. 13.2). Наикратчайший путь заканчивается в меньшем "ярусе" висячей вершины дерева, самый длинный путь заканчивается в наибольшем "ярусе" (ярусы отмечены на рисунке штриховыми линиями).
Число путей равно числу висячих вершин дерева, то есть 14. Длина кратчайшего пути (1,5,9) равна 2. Длина наиболее продолжительного пути равна 7. Длину пути помогает определить размещение каждой вершины дерева в соответствующем ярусе.
Этот пример, кстати, показывает, что понятие "длина пути" в теории графов не обязательно совпадает с понятием "длина пути" в геометрии или географии.
Рисунок дерева полезен не только тем, что позволяет подсчитать число всех возможных путей, отыскать среди них кратчайший и наиболее протяженный. Он позволяет еще одновременно "увидеть" все пути и сравнить их.