|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Виды подграфов
Пусть дан граф G = (X, A), где X = {хi}, i = 1, 2, ..., n – множество вершин, A = { ai }, i = 1, 2, ..., m – множество дуг.
Подграфом G'= (X', A') исходного графа G называется такой граф G', для которого 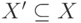 и
и 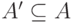 . Примеры подграфов показаны на
рис.
6.1,б, а исходный граф – на
рис.
6.1,а.
. Примеры подграфов показаны на
рис.
6.1,б, а исходный граф – на
рис.
6.1,а.
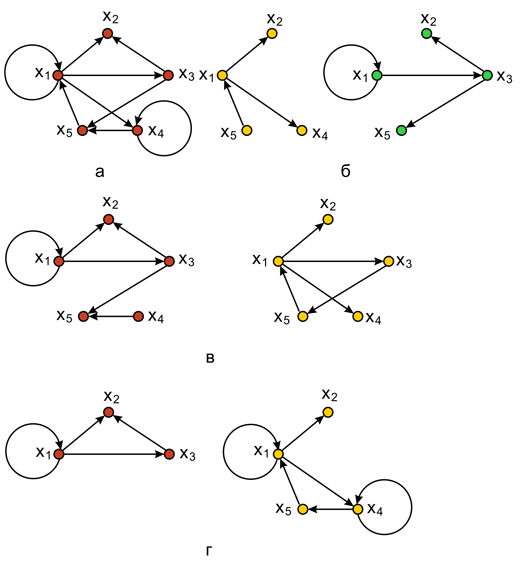
Рис. 6.1. Виды подграфов: а – исходный граф; б – подграфы; в – остовные подграфы; г – порожденные подграфы
Остовным подграфом Gp = (X, Ap ) графа G называется граф, для которого 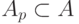 . Таким образом, остовный подграф имеет то же самое множество вершин, что и исходный граф G, но множество дуг подграфа Gp
является подмножеством множества дуг исходного графа. Примеры остовных подграфов приведены на
рис.
6.1,в. Для графа, имеющего m дуг, можно построить k остовных подграфов
. Таким образом, остовный подграф имеет то же самое множество вершин, что и исходный граф G, но множество дуг подграфа Gp
является подмножеством множества дуг исходного графа. Примеры остовных подграфов приведены на
рис.
6.1,в. Для графа, имеющего m дуг, можно построить k остовных подграфов
k=C1m+C2m+...+Cm-1m=2m-1
Порожденным подграфом Gs =(Xs , Гs ) называется граф, для которого 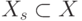 и для каждой вершины
и для каждой вершины 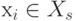 прямое отображение
прямое отображение 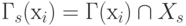 . Таким образом, порожденный подграф состоит из подмножества вершин Xs
множества вершин исходного графа и всех таких дуг графа G, у которого конечные и начальные вершины принадлежат подмножеству Xs
. Примеры порожденных подграфов приведены на
рис.
6.1,г.
. Таким образом, порожденный подграф состоит из подмножества вершин Xs
множества вершин исходного графа и всех таких дуг графа G, у которого конечные и начальные вершины принадлежат подмножеству Xs
. Примеры порожденных подграфов приведены на
рис.
6.1,г.
В качестве иллюстративного примера рассмотрим граф, вершины которого представляют сотрудников некоторого учреждения, а дуги – линии связи между сотрудниками. Тогда граф, представляющий только наиболее важные связи или каналы связи данного учреждения, является остовным подграфом; граф, который подробно описывает линии связи только какой-то части учреждения (например, отдела), является порожденным подграфом, а граф, который представляет только важные линии связи в пределах отдела, является просто подграфом.
Сильно связные графы и компоненты графа
Графы могут быть классифицированы по связности: сильно связные, односторонне связные, слабо связные и несвязные.
Орграф называется сильно связным, или сильным, если для двух любых различных его вершин хi и xj существует, по крайней мере, один путь, соединяющий эти вершины. Это определение означает также, что любые две вершины сильно связного графа взаимодостижимы. Пример данного графа показан на рис. 6.2,а.
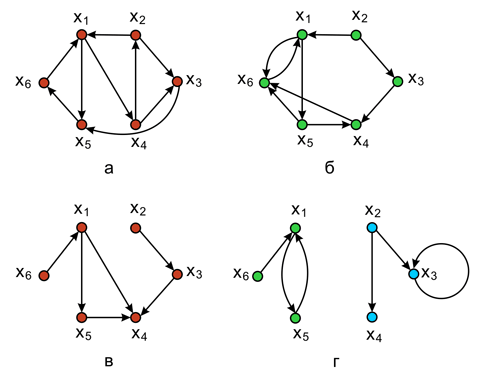
Рис. 6.2. Виды графов по связности: а – cильно связный граф; б – односторонне связный граф; в – cлабо связный граф; г – несвязный граф
Орграф называется односторонне связным, или односторонним, если для любых двух различных его вершин хi и xj существует, по крайней мере, один путь из хi в xj или из xj в хi или оба пути существуют одновременно. Граф на рис. 6.2,б не является сильным, так как в нем нет пути из х1 в х3 , но является односторонне связным.
Орграф называется слабо связным, или слабым, если для любых двух различных вершин графа существует по крайней мере один маршрут, соединяющий их. Граф, изображенный на рис. 6.2,в, не является ни сильным, ни односторонним, поскольку в нем не существует путей от х2 к х5 и от х5 к х2 . Он слабо связный.
Орграф называется несвязным, если для некоторой пары вершин орграфа не существует маршрута, соединяющего их ( рис. 6.2,г).
По признаку связности могут быть классифицированны и подграфы, но сначала введем понятие максимального подграфа. Пусть дано некоторое свойство Р, которым могут обладать графы.
Максимальным подграфом графа G относительно свойства Р называется порожденный подграф Gsm
, обладающий этим свойством и такой, что не существует другого порожденного графа Gs
, у которого 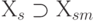 и который так же обладает свойством Р. Так, например, если в качестве свойства Р взята сильная связанность, то максимальным сильным подграфом графа G является сильный подграф, который не содержится ни в каком другом сильном подграфе. Такой подграф называется сильной компонентой графа. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента – максимальный слабый подграф.
и который так же обладает свойством Р. Так, например, если в качестве свойства Р взята сильная связанность, то максимальным сильным подграфом графа G является сильный подграф, который не содержится ни в каком другом сильном подграфе. Такой подграф называется сильной компонентой графа. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента – максимальный слабый подграф.
Например, в графе, приведенном на рис. 6.2,б, подграф, состоящий из вершин {х1, х4, х5, х6}, является сильной компонентой графа. С другой стороны подграфы, включающие вершины {х1, х6} и {х1, х5, х6}, не являются сильными компонентами (хотя и являются сильными подграфами ), поскольку они содержатся в графе, состоящем из вершин {х1, х4, х5, х6} и, следовательно, не максимальные. В графе, показанном на рис. 6.2,в, подграф не содержащий вершины {х1, х4, х5, х6}, является односторонней компонентой.
В графе, приведенном на рис. 6.2,г, оба подграфа, включающие вершины {х1, х5, х6} и {х2, х3, х4} являются слабыми компонентами, и у этого графа только две компоненты.
Из определений сразу же следует, что односторонние компоненты графа могут иметь общие вершины. Сильная компонента должна содержаться по крайней мере в одной односторонней компоненте, а односторонняя компонента содержится в некоторой слабой компоненте данного графа.
