Управление движением робота при помощи системы с отрицательной обратной связью
Релейный регулятор
Пример 9.1. Движение робота вдоль стены.
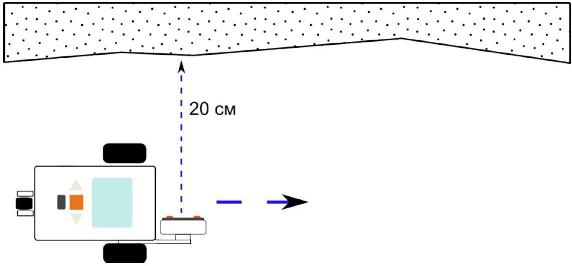
Пусть имеется робот, оснащённый датчиком ультразвука, и не очень ровная стена (с небольшими выступами и впадинами). Требуется написать программу управления движением робота вдоль стены на заданном расстоянии.
Следует заранее продумать положение датчика ультразвука. Как упоминалось выше (см. с. 38), этот датчик медленный. Поэтому его следует располагать чуть впереди корпуса робота. Кроме этого, его следует сместить как можно дальше от стены (см. Рис. 9.1), потому что на малых расстояниях (5 - 7 см) показания датчика ультразвука становятся слишком неточными. Далее мы увидим, что направление датчика также следует подкорректировать.
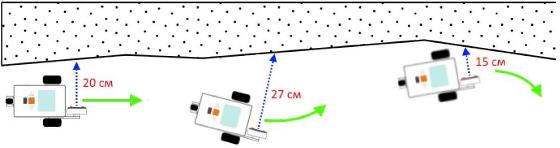
Алгоритм движения робота, записанный в словесной форме, может быть примерно таким (Рис. 9.2):
- двигаться прямо;
- если расстояние до стены больше заданного, то повернуть к стене;
- если расстояние до стены меньше заданного, то повернуть от стены;
- повторять шаги 2 - 3 бесконечно (или до наступления некоторого события).
Одним из самых очевидных решений этой задачи является релейный регулятор.
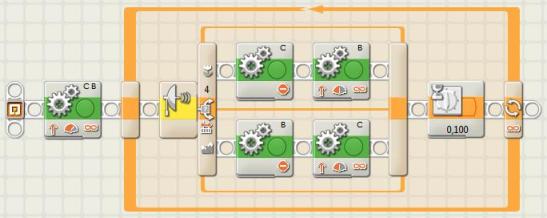
Для определённости примем в качестве заданного расстояния 20 см. Получим следующую программу (Рис. 9.3):
Как видно из текста программы, после включения обоих моторов запускается бесконечный цикл, в котором реализован вышеописанный словесный алгоритм. Хорошо заметной особенностью этого подхода является "рыскающее" движение: робот всегда поворачивает с одной и той же интенсивностью, независимо от того, насколько далеко или близко он оказался по отношению к стене. Поэтому траектория всегда будет зигзагообразной, так как во время поворотов робот всегда будет "прыгать" вокруг среднего значения 20 см. Так как датчик ультразвука является "медленным", в цикле используется небольшая задержка (0,1 с) для того, чтобы показания датчика успевали обрабатываться блоком NXT. Величина задержки фактически определяет время, в течение которого робот будет двигаться в неизменном направлении. Другими словами, увеличивая время задержки мы получим более крупные "зубцы" траектории. Как отмечалось ранее, делать задержку меньше 0,06 с не имеет смысла, потому что в этом случае датчик ультразвука просто не успеет провести измерения.
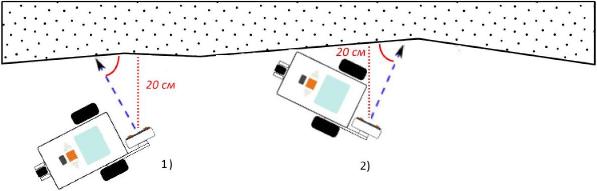
При использовании релейного регулятора возможны частые уходы робота с дистанции. Одна из причин состоит в том, что при выбранном нами расположении датчика ультразвука робот не сможет различать положения, симметричные относительно нормального положения. То есть два положения, показанные на Рис. 9.4 будут идентичными, и расстояние до стены в обоих случаях окажутся больше 20 см. В соответствии с вторым шагом алгоритма робот должен повернуть к стене (влево). И если для второго положения это верно, то для первого - ошибочно: робот ещё больше уйдёт с трассы.
Эту проблему можно решить, если расположить датчик не перпендикулярно к направлению движения (т. е. строго влево), а под углом 45° к направлению движения (Рис. 9.5).
Так нам удастся избежать случая, показанного на Рис. 9.4. Действительно, при подруливании влево расстояние до стены будет (при небольших углах поворота < 45°) уменьшаться, а при поворотах вправо, наоборот, увеличиваться. Однако не стоит рассчитывать, что наш робот сможет проехать вдоль стены любой формы. Даже простой поворот на 90° может вызвать у него неожиданные трудности. Таким образом, наиболее значимым достоинством релейного регулятора в нашем случае является простота его алгоритма. В следующем разделе мы рассмотрим более интересный алгоритм управления.
Задание 9.1. Запрограммируйте движение робота вдоль стены с разными положениями датчика ультразвука. В каком случае движение более устойчиво?
Задание 9.2. Сравните это решение с примером 4.1 на с. 48. Реализуйте релейный алгоритм движения вдоль стены без использования ветвления.
Задание 9.3. Реализуйте релейный алгоритм движения по линии с использованием ветвления.
P-регулятор
Трудности использования релейного регулятора, о которых говорилось в п. 9.1, требуют поиска более приемлемого решения задачи управления. Одним из вариантов является пропорциональный регулятор (или P-регулятор). В этом случае управляющее воздействие на моторы робота не постоянно, как в релейном регуляторе, а изменяется пропорционально отклонению от заданного расстояния до стены. Другими словами, чем больше отклонение, тем активнее должны работать моторы, выравнивая траекторию робота. В идеале робот должен ехать прямо, если датчик регистрирует заданное расстояние. При небольшом отклонении следует небольшое подруливание. Если отклонение больше, то и подруливание больше. Алгоритм P-регулятора является классическим в теории систем автоматического управления.
Пример 9.2. Управление движением вдоль стены на основе P-регулятора.
Для P-регулятора управляющее воздействие U(t) на моторы робота в момент времени t вычисляется по формуле:
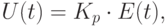 |
( 9.1) |
где
-
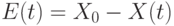 - отклонение робота от заданного положения (другими словами, ошибка, Error, или ещё говорят невязка);
- отклонение робота от заданного положения (другими словами, ошибка, Error, или ещё говорят невязка);
-
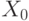 - заданное расстояние до стены (у нас 20 см);
- заданное расстояние до стены (у нас 20 см);
-
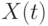 - текущее показание датчика;
- текущее показание датчика;
-
 - усиливающий коэффициент (коэффициент пропорциональности). Всегда положительный.
- усиливающий коэффициент (коэффициент пропорциональности). Всегда положительный.
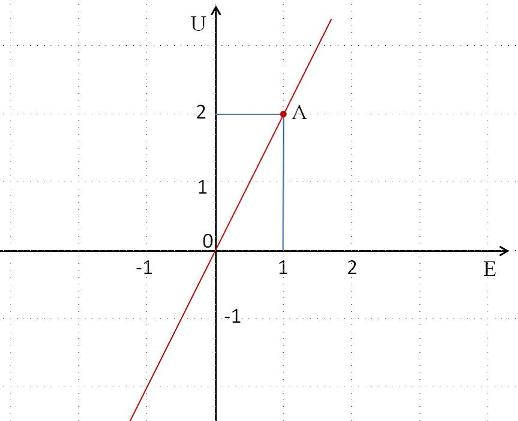
Очевидно, графиком для расчёта управляющего воздействия U в зависимости от ошибки E будет прямая (см. Рис. 9.6):
Из графика очень просто определить коэффициент  . Выберем произвольную точку на графике. В нашем случае это точка A(1; 2). Тогда
. Выберем произвольную точку на графике. В нашем случае это точка A(1; 2). Тогда
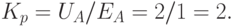
Ошибка может быть как положительная (если мы ближе к стене, чем надо), так и отрицательная (если мы отъехали от стены дальше, чем необходимо). Таким образом, управляющее воздействие U(t) тоже может быть как положительным, так и отрицательным.
Пусть мы имеем P-регулятор для робота, движущегося вдоль стены. Тогда мощность моторов PowerB(t) и PowerC(t) в момент времени t вычисляется по формулам:
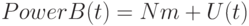 |
( 9.2) |
 |
( 9.3) |
где
- Nm - нормальная мощность моторов: мощность, с которой должны крутиться оба двигателя, если отклонение от курса равно нулю. В нашей программе можно положить Nm = 50;
- U(t) - управляющее воздействие на моторы, вычисляемое по формуле (9.1).
Рассмотрим смысл коэффициента пропорциональности  . Как видно, поворот производится в силу того, что от мощности одного мотора управляющее воздействие вычитается, тогда как к другому - прибавляется. Таким образом коэффициент
. Как видно, поворот производится в силу того, что от мощности одного мотора управляющее воздействие вычитается, тогда как к другому - прибавляется. Таким образом коэффициент  может усиливать или ослаблять воздействие регулятора на моторы: если он больше единицы, то происходит усиление, а если меньше - ослабление. Большой
может усиливать или ослаблять воздействие регулятора на моторы: если он больше единицы, то происходит усиление, а если меньше - ослабление. Большой  сделает робот очень чутким к ошибкам, что приведёт к резким рывкам для исправления траектории. Малый
сделает робот очень чутким к ошибкам, что приведёт к резким рывкам для исправления траектории. Малый  сделает движения робота плавнее, но на крутых поворотах робот может потерять стену и сойти с траектории. Конкретные значения коэффициента
сделает движения робота плавнее, но на крутых поворотах робот может потерять стену и сойти с траектории. Конкретные значения коэффициента  , наиболее подходящие в каждом конкретном случае, будут зависеть от конструктивных особенностей робота, скорости движения (нормальной мощности), сложности трассы, используемых датчиков. Величины PowerB(t) и PowerC(t) должны лежать в диапазоне [0; 100]. Поэтому при больших ошибках (и, соответственно, больших управляющих сигналах) мощность моторов будет ограничиваться так, чтобы она не выходила из указанного диапазона. В этом случае пропорциональный регулятор не будет работать корректно, поскольку не сможет скомпенсировать большие ошибки. Таким образом, одной из особенностей P-регулятора является адекватная работа только при небольших ошибках. Для того, чтобы учесть это в нашей задаче нужно иметь стену без резких поворотов и двигаться с небольшой скоростью.
, наиболее подходящие в каждом конкретном случае, будут зависеть от конструктивных особенностей робота, скорости движения (нормальной мощности), сложности трассы, используемых датчиков. Величины PowerB(t) и PowerC(t) должны лежать в диапазоне [0; 100]. Поэтому при больших ошибках (и, соответственно, больших управляющих сигналах) мощность моторов будет ограничиваться так, чтобы она не выходила из указанного диапазона. В этом случае пропорциональный регулятор не будет работать корректно, поскольку не сможет скомпенсировать большие ошибки. Таким образом, одной из особенностей P-регулятора является адекватная работа только при небольших ошибках. Для того, чтобы учесть это в нашей задаче нужно иметь стену без резких поворотов и двигаться с небольшой скоростью.
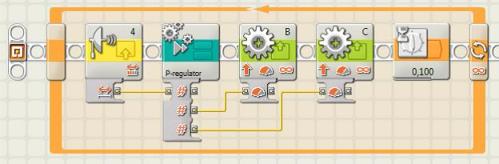
Реализуем алгоритм P-регулятора согласно приведённым формулам при помощи вложенных процедур (My blocks) на языке NXT-G.
Блок вычисления отклонения (ошибки) от заданного расстояния, который мы назовём Error, имеет следующие параметры:
- входные - текущее показание датчика расстояния X(t);
- выходные - ошибка E(t)).
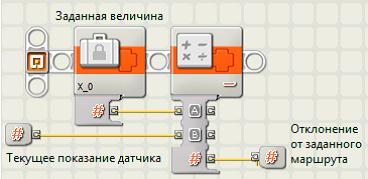
Блок Error на языке NXT-G выглядит так:
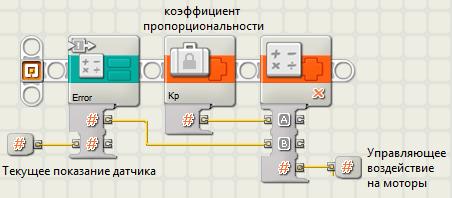
Мы используем его в подпрограмме для вычисления управляющего воздействия U(t). Она имеет следующие параметры:
- входные - текущее показание датчика X(t);
- выходные - управляющее воздействие на моторы.
Этот блок мы используем для разработки блока P-регулятора. Он будет иметь следующие параметры:
- входные - текущее показание датчика;
- выходные - мощность моторов B и C.
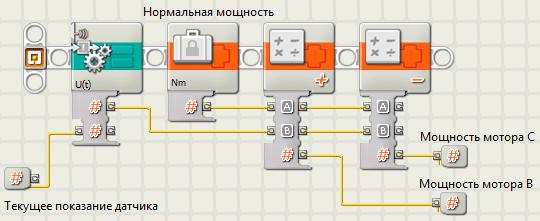
Наконец, полная программа, реализующая бесконечное движение вдоль стены, получается с использованием блока P-регулятора и формул (9.2) и (9.3):
Задание 9.4. Реализуйте предложенный алгоритм движения вдоль стены с использованием P-регулятора. Проверьте его работу. Настройте регулятор при помощи подбора коэффициента  .
.
Задание 9.5. Реализуйте алгоритм следования по линии с использованием P-регулятора. Настройте регулятор, добиваясь наиболее уверенного прохождения роботом крутых поворотов.
Задание 9.6. Проведите соревнование в своей группе да скоростное прохождение трассы.
Задание 9.7. После того, как робот стал двигаться по линии более или менее уверенно, попробуйте (1) увеличить подобранный коэффициент  вдвое; (2) уменьшить подобранный коэффициент
вдвое; (2) уменьшить подобранный коэффициент  вдвое. Как изменяется характер движения робота? Удаётся ли ему пройти трассу? Какие участки наиболее проблемны?
вдвое. Как изменяется характер движения робота? Удаётся ли ему пройти трассу? Какие участки наиболее проблемны?
Задание 9.8. Реализуйте алгоритм следования за рукой с использованием P-регулятора (см. задание 5.4 на с. 63). Настройте регулятор так, чтобы движение робота стало как можно более плавным.
Тем не менее, использование P-регулятора не позволяет решить задачу полностью: движение робота будет сильно зависеть от его конструкции, настроек регулятора и пр. Чтобы движение стало ещё стабильнее, нужно обратиться к более интеллектуальным алгоритмам. В первую очередь здесь следует назвать пропорционально-дифференциальный (PD) и пропорционально-интегрально-дифференциальный (PID) регуляторы. В настоящем пособии начального уровня указанные алгоритмы изучаться не будут. Интересующихся мы отсылаем к книге С. А. Филиппова [6], где подробно рассмотрены эти и другие интереснейшие задачи.