Нелинейная динамика и синергетика. Искусственный интеллект
На самом деле с такими постановками задач мы сталкивались уже в школьной программе изучая физические эксперименты, в которых измеряется результат того или иного воздействия на систему. Например, прикладывая к пружине разные усилия, мы получаем разные длины растяжения или сжатия. Но полученные результаты — это не произвольные числа, они определяются характеристиками (параметрами) самой пружины (коэффициентом упругости). Кроме того, на результат влияют и конкретные условия проведения эксперимента, определяемые внешними силами, помехами и т.п. (в частности, трение).
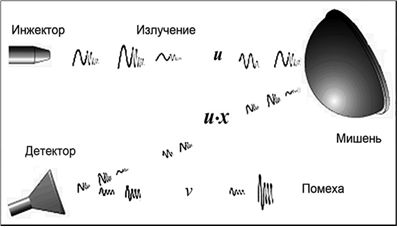
Другой типичный пример из области исследования материалов, или недр, или разнообразных применений дистанционного зондирования показан на рис. 2.8.
Источник посылает в пространство некоторый сигнал  (излучение), или поток частиц (электроны, или
(излучение), или поток частиц (электроны, или  -частицы и т.п.), или волну той или иной природы (акустическую или электромагнитную), причем интенсивность потока можно варьировать и точно измерять (например, мерить величину "ушедшего" заряда). При встрече с мишенью либо сигнал отражается (эхо-акустика, радар и т.п.), либо его взаимодействие с мишенью порождает некоторый новый "отраженный" сигнал
-частицы и т.п.), или волну той или иной природы (акустическую или электромагнитную), причем интенсивность потока можно варьировать и точно измерять (например, мерить величину "ушедшего" заряда). При встрече с мишенью либо сигнал отражается (эхо-акустика, радар и т.п.), либо его взаимодействие с мишенью порождает некоторый новый "отраженный" сигнал 
 (может быть и другой природы), интенсивность которого потом измеряется детектором. Требуется определить неизвестный параметр
(может быть и другой природы), интенсивность которого потом измеряется детектором. Требуется определить неизвестный параметр  , который либо равен нулю, что соответствует отсутствию мишени с заданными отражающими свойствами, либо при положительной величине
, который либо равен нулю, что соответствует отсутствию мишени с заданными отражающими свойствами, либо при положительной величине  характеризует те или иные физические характеристики: дальность до мишени, ее размер, отражающие свойства материала и т. п.
характеризует те или иные физические характеристики: дальность до мишени, ее размер, отражающие свойства материала и т. п.
Общим в рассмотренных примерах является возможность активного влияния экспериментатора на результат наблюдений (возможность подать "входное воздействие").
В каком максимально широком классе помех  все-таки реалистично попытаться получить осмысленный ответ в задаче об оценивании неизвестного параметра x?
все-таки реалистично попытаться получить осмысленный ответ в задаче об оценивании неизвестного параметра x?
Естественно при записи уравнения, задающего модель наблюдений, предположить, что второе слагаемое в правой части  включает в себя все неопределенности, влияющие на выход
включает в себя все неопределенности, влияющие на выход 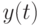 , которые никак не связаны с
, которые никак не связаны с  , т.к.
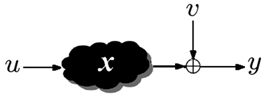
, т.к.  явно входит только в первое слагаемое в правой части. Такие помехи будем называть "внешними", подчеркивая их независимость от внутренних входов, подаваемых в систему. Можно ли как-то решить задачу в таком классе неопределенностей? Поясним схему задачи, используя рис. 2.9.
явно входит только в первое слагаемое в правой части. Такие помехи будем называть "внешними", подчеркивая их независимость от внутренних входов, подаваемых в систему. Можно ли как-то решить задачу в таком классе неопределенностей? Поясним схему задачи, используя рис. 2.9.
Система является "черным ящиком" с входом  и выходом
и выходом 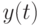 . Система характеризуется неизвестным нам параметром
. Система характеризуется неизвестным нам параметром  (например, в примере с пружиной
(например, в примере с пружиной  — это коэффициент упругости). Экспериментатор может выбирать воздействия на систему
— это коэффициент упругости). Экспериментатор может выбирать воздействия на систему  , которые поступают на вход "черного ящика" (в примере с пружиной мы можем растянуть или сжать ее на расстояние
, которые поступают на вход "черного ящика" (в примере с пружиной мы можем растянуть или сжать ее на расстояние  ). На выходе "черного ящика" к результату добавляется внешняя помеха
). На выходе "черного ящика" к результату добавляется внешняя помеха  , которая никак не связана с "внутренними" процессами внутри "черного ящика" (в примере с пружиной выход с помехой — погрешности измерений, вносимые динамометром).
, которая никак не связана с "внутренними" процессами внутри "черного ящика" (в примере с пружиной выход с помехой — погрешности измерений, вносимые динамометром).
Уточним задачу. Требуется по последовательности входов и выходов 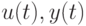 определить неизвестный параметр
определить неизвестный параметр  при отсутствии каких-либо ограничений на последовательность внешних помех
при отсутствии каких-либо ограничений на последовательность внешних помех  .
.
Не кажется ли такая постановка задачи абсурдной?
С детерминистской точки зрения — конечно! Не может быть никакого детерминированного алгоритма, дающего хотя бы в каком-то смысле здравый ответ (кроме бессмысленного решения — вся числовая ось!). Предложив в качестве ответа любое из чисел или даже какой-то интервал при конечном (или счетном) числе наблюдений, всегда можно будет подобрать такие  , что при следующем наблюдении предложенный ответ будет неверным.
, что при следующем наблюдении предложенный ответ будет неверным.
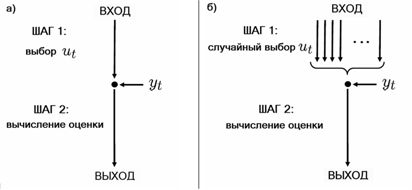
Общий алгоритм последовательного оценивания неизвестного параметра  состоит из двух шагов:
состоит из двух шагов:
1. Выбор входа  .
.
2. Оценивание параметра x на основе полученных данных  ,
, 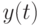 (например, вычисление числовой оценки
(например, вычисление числовой оценки  или множества
или множества  , содержащего
, содержащего  ).
).
Если бы в условиях задачи дополнительно можно было бы предположить случайную (вероятностную) природу помех  , то при выполнении условий закона больших чисел можно было бы говорить об оценивании неизвестного параметра x путем простого усреднения данных наблюдения.
, то при выполнении условий закона больших чисел можно было бы говорить об оценивании неизвестного параметра x путем простого усреднения данных наблюдения.
Если наблюдения проводить также со случайной помехой, но у которой среднее значение  было бы неизвестно, то результаты усреднения отличались бы от истинного значения x, на неизвестную величину
было бы неизвестно, то результаты усреднения отличались бы от истинного значения x, на неизвестную величину  .
.
Несмотря на кажущуюся абсурдность постановки задачи оценивания при произвольных внешних помехах, из практических потребностей часто ее все-таки приходится решать.
Альтернативой оказываются рандомизированные алгоритмы, в которых выполнение одного или нескольких шагов производимых пользователем основано на случайном правиле (т.е. среди многих детерминированных правил одно вы-бирается случайно в соответствии с вероятностью 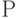 ).
).
В зависимости от специфики конкретной задачи вероятность 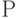 или является искусственным элементом, вводимым в алгоритм для улучшения разрешимости проблемы, или в рассматриваемой системе могут присутствовать измеряемые случайные элементы. Выбор этой вероятности
или является искусственным элементом, вводимым в алгоритм для улучшения разрешимости проблемы, или в рассматриваемой системе могут присутствовать измеряемые случайные элементы. Выбор этой вероятности 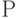 является частью конструирования алгоритма.
является частью конструирования алгоритма.
Рассмотрим следующее правило случайного выбора для первого шага рандомизированного алгоритма последовательного оценивания неизвестного параметра 

На втором шаге по известным парам значений 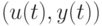 формируем величины
формируем величины 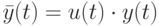 . Для "новой" последовательности наблюдений справедлива похожая на исходную модель
. Для "новой" последовательности наблюдений справедлива похожая на исходную модель
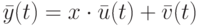
в которой 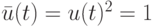 ,
, 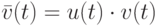 .
.
Если  — внешние помехи, то естественно считать, что они независимы с нашим рандомизированным правилом выбора входов на шаге 1. Следовательно,
— внешние помехи, то естественно считать, что они независимы с нашим рандомизированным правилом выбора входов на шаге 1. Следовательно,
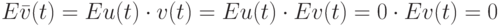
т.е. "в новой модели" наблюдений задача об оценивании неизвестного параметрa x, не имевшая решения, превращается при использовании случайного правила выбора входов на шаге 1 рандомизированного алгоритма в "стандартную" задачу об оценивании неизвестного параметра x, наблюдаемого на фоне независимых центрированных помех (рис. 2.10).
В упоминавшейся выше книге О.Н. Граничина и соавторов приведены алгоритмы, обоснования и примеры численного моделирования, дающие при фиксированном малом (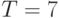 ) количестве наблюдений доверительные интервалы для x с задаваемой априорно вероятностью Р.
) количестве наблюдений доверительные интервалы для x с задаваемой априорно вероятностью Р.