Архитектура ЭВМ
[+]
Опубликован: 08.11.2022 | Доступ: свободный | Студентов: 80 / 0 | Длительность: 06:05:00
Тема: Аппаратное обеспечение
Лекция 7:

Логические схемы на примере двоичного сумматора
A
|
версия для печати
< Лекция 6 || Лекция 7: 12 || Лекция 8 >

64-битный сумматор реализуется как два 32-битных - один для младшей 32-битной секции числа, а другой - для старшей. Младшая секция, представляющая собой обычный 32-битный сумматор, складывает биты 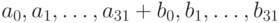a_0, a_1, \dots, a_{31}+b_0, b_1, \dots, b_{31} и выдаёт биты суммы 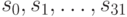s_0, s_1, \dots, s_{31}, а также бит переноса 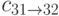c_{31 \to 32}. Старшая секция складывает с учётом переноса 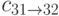c_{31 \to 32} старшие биты 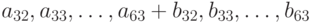a_{32},a_{33},\dots, a_{63}+b_{32}, b_{33}, \dots, b_{63}. 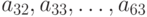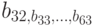Но чтобы не ждать переноса из младшей секции, старшая организована следующим образом: она состоит из двух 32-битных сумматоров, получающих на вход одни и те же слагаемые a_{32},a_{33},\dots, a_{63} и b_{32, b_{33},\dots,b_{63}, и при этом один из сумматоров всегда получает бит переноса 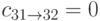c_{31 \to 32}=0, а другой - 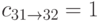c_{31 \to 32}=1. Сумматоры старшей секции "запускаются" одновременно друг с другом и с сумматором младшей, и одновременно с ней заканчивают работу. 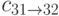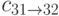К моменту окончания работы этих трёх 32-битных сумматоров (одного "младшего" и двух "старших") становится известно действительное значение переноса c_{31 \to 32}, и в итоговую сумму попадают результирующие биты лишь одного из "старших" сумматоров - того, который работал в условиях верного предположения значения входящего переноса c_{31 \to 32}.

Описанный подход можно описать словами: "Сделай всё, что можешь, как можно скорее, часть из этого пригодится, остальное выбросим". Такая стратегия вычислений называется спекулятивной. Спекулятивность усложняет сумматор в нашем примере: она приводит к тому, что, фактически, результаты 1/3 вычислений (одного из трёх 32-разрядный сумматоров) выполняются впустую. Тем не менее она популярна, так как позволяет ускорить работу сумматора почти вдвое. Иногда сумматоры делят и на бо?льшее число секций.

Арифметикло-логическое устройство

Сумматор, мультипликатор (логическая схема для умножения двоичных чисел), а также модули для выполнения логических операций и некоторые другие логические схемы составляют арифметико-логическое устройство (АЛУ), которое является одним из основных блоков процессора.

О важности арифметических и логических операций мы уже говорили в прошлой лекции. Арифметико-логическое устройство - это функциональный блок процессора, который, по сравнению с обычным сумматором, можно считать своеобразным "швейцарским ножом": "снаружи" он во многом напоминает обычный сумматор, но функциональность у него гораздо шире. С остальными блоками процессора его связывают следующие входы и выходы:

  1. как и у обычного сумматора, у АЛУ имеется два входа для первого и второго аргументов бинарных операций (например, сложения или умножения); для унарных операций (изменение знака, логическое отрицание) используется один из них;
  2. как и у обычного сумматора, у АЛУ имеется выход для результата операции;
  3. как и у обычного сумматора, у АЛУ имеется вход и выход переноса;
  4. АЛУ также имеет управляющий вход, задающий, какую именно следующую операцию следует выполнить , то есть какой из инструментов швейцарского ножа нужно сейчас использовать.

В зависимости от значения на управляющем входе (4) ко входам и выходам (1-3) подключается та или иная логическая схема, входящая в состав АЛУ:

  • сумматор,
  • побитовые логические операции,
  • побитовый сдвиг,
  • мультипликатор и пр.

Сделаем небольшой обзор реализаций упомянуты арифметико-логических операций.

Сложение выполняется при помощи сумматора. Вычитание выполняется также сумматором, поскольку очевидным образом выражается через сложение, как мы обсуждали в предыдущих лекциях.

Побитовые логические операции - это операции, которые выполняются побитово, например, побитовое отрицание двоичного числа выполняет отрицание каждого его бита, побитовая операция "и" двух чисел выполняет "и" для каждой пары соответствующих битов и т.д. Таким образом, для побитовое отрицание, получая на вход 32-битовое двоичное число 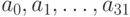a_0, a_1, \dots, a_{31}, выдает следующий результат: \neg a_0, \neg a_1, \dots, \neg a_{31}. 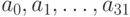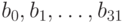Побитовое "и" (операция & в языке С), получая на вход два 32-битовых числа получая на вход 32-битовое двоичное число a_0, a_1, \dots, a_{31} и b_0, b_1, \dots, b_{31}, выдаёт число 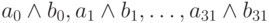a_0 \wedge b_0, a_1 \wedge b_1, \dots, a_{31} \wedge b_{31}. Аналогично действуют и другие побитовые операции - "или", "исключающее или" и т.д. Поскольку, в отличие от сумматора, все биты обрабатываются независимо, проблем с задержкой переноса не возникает, и побитовые операции всегда выполняются за один такт.

Сдвиг двоичного числа - это операция, смещающая разряды (биты) числа от младшего к старшему, дописывая справа нуль и теряя старший бит (левый сдвиг, обозначается "<<" в языке C) или от старшего к младшему, дописывая слева ноль и теряя младший бит (правый сдвиг, ">>" в языке C). Для того, чтобы сдвинуть аргумент a на 1 бит влево АЛУ присоединяет выходные биты к соответствующим входным. Сдвиг числа влево на 1 бит эквивалентен умножению на 2, но выполняется намного быстрее. Аналогично работает сдвиг вправо, и он эквивалентен делению на 2 нацело. Поскольку при сдвигах АЛУ всего лишь соединяет выходы с соответствующими входами, сдвиги, так же, как и побитовые операции, выполняются за один такт. Отметим, что современные AЛУ за один такт умеют сдвигать числа и на произвольное количество битов, а также выполнять некоторые другие разновидности сдвигающих биты операций.

Умножение выполняется мультипликатором. Если мы вспомним алгоритм умножения "в столбик", то увидим, что он состоит из сдвигов, сложений и умножений на одноразрядное число. В случае двоичной системы умножение на одноразрядное число реализуется тривиально: поскольку одноразрядное число может быть либо 0, либо 1, то и произведение будет равно или другому множителю, или нулю. Таким образом, мультипликатор также можно изготовить в виде логической схемы. Но она получится весьма громоздкой: в ней будет уже очень много вентилей и связей между ними. Поэтому в некоторых АЛУ операция умножения выполняется не единой логической схемой, а как последовательность микроопераций (про микрооперации мы расскажем в следующих разделах) с запоминанием промежуточных результатов в специальных внутренних регистрах, используемых только в АЛУ. Чтобы лучше представить себе работу такого АЛУ, попробуйте написать программу на любом языке программирования, которая умножает два числа, пользуясь для этого лишь операциями сдвига и сложения. По аналогии с умножением, деление также можно реализовать при помощи логической схемы, но она получится ещё сложнее, поэтому деление также часто реализуется в виде последовательности микроопераций.

Отметим, что программная реализация умножения, которую мы предлагаем выполнить читателям - отнюдь не просто "учебное" упражнение. АЛУ некоторых простых процессоров, например, Intel 8080, позволяло выполнять лишь сложение, вычитание, сдвиг и побитовые операции, а умножение для этих процессоров действительно приходилось реализовывать уже программистам.

Вопросы

  1. Что такое арифметико-логическое устройство?
  2. Почему велика его роль в устройстве процессора?
  3. Что такое одноразрядный сумматор?
  4. Постройте таблицу истинности одноразрядного сумматора.
  5. Постройте логическую схему одноразрядного сумматора.
  6. Проверьте правильность работы одноразрядного сумматора при различных входных значениях 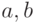a,b и c.
  7. Постройте на основе нескольких 1-разрядных сумматоров один 4-разрядный сумматор.
  8. Объясните, что такое многоразрядный сумматор.
  9. Для чего используются сумматоры в ЭВМ?
  10. Назовите узкое место многоразрядных сумматоров.
  11. Опишите способ оптимизации переноса в многоразрядном сумматоре.
  12. Что такое спекулятивные вычисления?
  13. Что такое АЛУ и какие операции оно может выполнять?
  14. Перечислите входы АЛУ.
  15. Перечислите выходы АЛУ.
  16. Что такое побитовые логические операции?
  17. Расскажите про реализацию побитовых логических операций.
  18. Что такое побитовый сдвиг?
  19. Расскажите про реализацию побитового сдвига.
  20. Расскажите про реализацию в АЛУ умножения.

Литература

  1. Орлов С.А., Цилькер Б.Я. Организация ЭВМ и систем: Учебник для вузов. 2-е изд. СПб.: Питер, 2011. 688 с.
  2. Харрис Д.М., Харрис С.Л. Цифровая схемотехника и архитектура компьютера. [пер. с англ.] Imagination Technologies. М.: ДМК Пресс, 2018. 792 с.
  3. Таненбаум Э., Остин Т. Архитектура компьютера. 6-е изд. СПб.: Питер, 2013. 816 с.
Дальше >>
< Лекция 6 || Лекция 7: 12 || Лекция 8 >

Вопросы и ответы

вопросов: 1
Наталья Ра
Наталья Ра

Здравствуйте! Когда появится возможность сдать экзамен на сертификат?

ответить