Основы схемотехники

Булевы функции; таблицы истинности булевых функций, система базовых булевых функций; вентили.

Булевы функции

Пусть B=/{0.1/}. Тогда n-местной булевой функцией будем называть функцию, действующую из 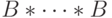в B.

Рассмотрим следующие простейшие булевы функции.

• - "и" (конъюнкция), выдает 1, когда оба аргумента равны 1. Иначе выдает 0.
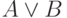• - "или" (дизъюнкция) выдает 1, когда хотя бы один аргумент равен 1. Иначе выдает 0.
• - "не" (отрицание) обозначается 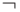) - выдает 1, если аргумент 0, и 0, если аргумент равен 1.
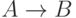• - "импликация", выдаёт 0, когда первый аргумент 1, а второй 0 (то есть из истины не может следовать ложь), а в остальных случаях выдает 1.
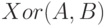• (другой вариант записи - ) - "исключающее или" (сложение по модулю 2), выдает 1, когда ровно один аргумент равен 1, в остальных случаях выдает 0.

Таблицы истинности булевых функций

Булевы функции, в отличие от функции в математическом анализе, являются дискретными. Более того, количество возможных уникальных сочетаний аргументов, а также соответствующих им значений, является небольшим и может быть перечислено явно.

Значения булевых функций в соответствии со значениями их аргументов можно представить при помощи таблиц истинности. Каждая строка такой таблицы соответствует сочетанию аргументов и соответствующему значению функции.

Таблица 6.1 представляет таблицы истинности для ряда известных булевых функций.

Таблица 6.1. Таблицы истинности для некоторых простейших булевых функций.

A	B				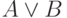Xor (A,B)
0	0	0	0	1	0
0	1	0	1	1	1
1	0	0	1	0	1
1	1	1	1	0	0

Система базовых булевых функций

Существует следующая важная теорема.

Теoрема 1. Любая булева функция может быть представлена в виде суперпозиции следующих булевых функций - "и", "не" или "и", "или".

Несмотря на то, что хватает двух функций из трех, для представления произвольной булевой функции удобно использовать все эти три функции (в этом, кстати, заключается идея доказательства приведённой выше теоремы).

Например, .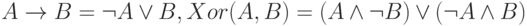

Набор булевых функций, с помощью которого можно выразить все остальные булевы функции, будем называть системой базовых булевых функций.

Наборы \{"и", "не"\} и \{"или", "не"\} являются системами базовых булевых функций. Следует отметить, что существуют и другие аналогичные системы. Например, каждая из приведенных ниже функций образует базовую систему булевых функций (то есть каждая из этих систем состоит из одной единственной функции).

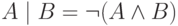• - штрих Шефера ("и-не").
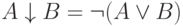• - стрелка Пирса ("и-или").

Нетрудно доказать, что других систем базовых функций, состоящих всего лишь из одной функции, больше нет.

Вентили и логические схемы

Теперь перейдём от булевых функций к внутреннему устройству компьютеров с - к вентилям, логическим схемам, функциональным блокам процессора и командам машинного языка.

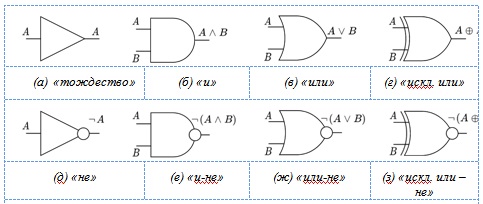
Физическая реализация простейшей булевой функции с помощью полупроводниковых элементов (транзисторов, резисторов, диодов и пр.) называется вентилем (gate).

Таким образом, вентили являются элементарными логическими схемами, и более сложные схемы, реализующие различные функциональные блоки процессора, строятся на их основе.

На рис.6.1 приведены обозначения основных логических вентилей в соответствии со стандартом ANSI/IEEE 91-1984. ANSI (American National Standards Institute) - американский институт, который осуществляет надзор за разработкой и использованием различных компьютерных стандартов. Так вот, в стандарте ANSI/IEEE 91-1984 описаны графические изображения как вентилей, так и для более сложных логических схем, а также некоторых других схем цифровой электроники. Исторически он базируется на стандартах министерства обороны США 1950-х-60-х годах - вентили ранних ЭВМ создавались на базе ламп и электромеханических реле, но обозначались на схемах аналогичным образом. Сейчас этот стандарт является международным и используется в различных сферах производства.

Теперь определим более сложный элемент под названием логическая схема.

Логическая схема - это преобразователь, которому на вход подается некоторый двоичный вектор, а его выходом служит также некоторый (но уже другой!) двоичный вектор.

Процессор состоит из набора функциональных блоков, таких как арифметико-логическое устройство, устройство чтения машинного кода, набор регистров, кэш-память и т.д. В свою очередь, эти функциональные блоки состоят из множества различных логических схем.

При построении логических схем используют атомарные элементы - вентили, которые являются реализацией простейших булевых функций. Демонстрация этого факта будет проведена в следующей лекции. Однако уже теперь мы проведем некоторую подготовку.

Для работы основных функций процессора очень важны логико-арифметические операции. С их помощью реализуются важнейшие составные команды процессора: загрузка/выгрузка в оперативную память, присваивание, условные переходы, циклы и пр. Кроме того, различные математические функции (например, log или sin) обычно вычисляются современными процессорами при помощи частичного суммирования рядов Тейлора. Такие вычисления требуют не только непосредственно арифметических операций, но также используют циклы, следовательно, и логические операции. В свою очередь, математические функции используются для обработки мультимедиа данных - изображений, видео, звука. Разумеется, используются они и при выполнении ЭВМ своего "исходного предназначения" - физических и математических расчётов.

Итак, логические операции у нас имеются - это булевы функции, реализуемые вентилями. А то, как обстоит дело с арифметическими операциями, будет показано в следующей лекции, где описывается логическая схема для сложения (сумматора).

Ну и, наконец, относительно небольшой набор вентилей может напомнить нам систему базовых булевых функций. С той разницей, что в такую систему добавлено больше функций, чем содержит минимальная система базовых функций, поскольку требуется строить реальные (не теоретические) логические схемы и нужны удобные строительные блоки, реализующие наиболее часто встречающиеся операции.

Рис. 6.1. Схематическое изображение вентилей в соответствии со стандартом ANSI/IEEE 91-1984

Вопросы

1. Дайте определение булевой функции.
2. Что такое таблица истинности? Приведите примеры.
3. Докажите, пользуясь таблицами истинности, что 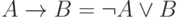и .
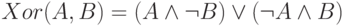4. Что такое система базовых булевых функций?
5. Докажите с помощью таблиц истинности, что любую булеву функцию можно представить как суперпозицию функций из системы \{"и", "не"\}.
6. Сделайте тоже для системы функций \{"или", "не"\}.
7. Докажите, что стрелка Пирса являются системами базовых булевых функций.
8. Докажите, что штрих Шефера являются системами базовых булевых функций.
9. Докажите, что стрелка Пирса и штрих Шефера являются единственными системами базовых булевых функций, состоящих из одной функции.
10. Что такое вентиль?
11. Приведите примеры вентилей.
12. Что такое логическая схема?
13. Постройте логическую схему "исключающее или" на основе вентилей "и", "или" и "не".
14. Почему для процессоров важны логико-арифметические операции?

Литература

1. Харрис Д.М., Харрис С.Л. Цифровая схемотехника и архитектура компьютера. [пер. с англ.] Imagination Technologies. М.: ДМК Пресс, 2018. 792 с.
2. Таненбаум Э., Остин Т. Архитектура компьютера. 6-е изд. СПб.: Питер, 2013. 816 с.
3. IEEE Standard Graphic Symbols for Logic Functions (Including and incorporating IEEE Std 91a-1991, Supplement to IEEE Standard Graphic Symbols for Logic Functions) // IEEE Std 91a-1991 & IEEE Std 91-1984, 1984, С. 1-160.