|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Опубликован: 02.03.2017 | Доступ: свободный | Студентов: 2512 / 557 | Длительность: 21:50:00
Тема: Безопасность
Лекция 7:
Современные симметричные алгоритмы шифрования
7.3 Исследование устойчивости блочных шифров
Для количественного анализа устойчивости процедур преобразования данных в ходе шифрования используется их представление в виде структур, состоящих из булевых функций. Этот же метод позволяет оценивать зависимость криптостойкости шифрования от выбранной ключевой информации, определяя, таким образом, критерии выбора "сильных" ключей и блоков замен (в случае ГОСТ 28147-89 и других, менее распространенных шифров с секретными блоками замен).Здесь мы кратко изложим метод исследования устойчивости алгоритма блочного шифрования к наиболее распространенным атакам, подробнее см. [2].
7.3.1 Количественные характеристики устойчивости шифрования
Определение 7.1 Булевой функцией называется отображение 
, то есть правило, однозначно сопоставляющее вектору из 
бит значение 0 или 1.
Способы задания булевой функции [2]:
1) Табличный -- в виде таблицы, каждая строка которой задает значение функции при определенном наборе значений входных переменных. Число строк такой таблицы равно 
.
Пример 7.1 Таблица 7.2 задаёт булеву функцию 
.
 |
 |
 |
|
|---|---|---|---|
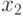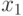| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
2) Векторный -- в виде вектора, состоящего из значений булевой функции, выписанных в порядке возрастания аргумента, если его представить в виде числа от 0 до 
. В самом деле, вместо логических переменных 
в качестве аргумента функции можно использовать -битное целое число
Функция из примера 1 в векторном виде будет представлена следующим образом: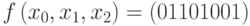 
(последний столбец таблицы выписан сверху вниз).
3) Аналитический -- в виде формулы, выражающей зависимость значения функции от значений ее аргументов.
Функция из примера 7.1 в аналитическом виде можно представить следующим образом: 
, где 
- операция сложения бит по модулю 2 (XOR).
Определение 7.2 Весом булевой функции называется количество наборов значений входных переменных, при которых она принимает значение 1.
Проще говоря, это число единиц в векторном представлении булевой функции. Так, вес функции из примера 1 равен 4 (так как из 8 бит в векторе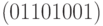 
4 единицы). Обозначается 
, например, 
.
Определение 7.3 Расстоянием между двумя булевыми функциями называется вес их побитовой суммы по модулю 2 в векторном виде (число позиций вы векторах, в которых значения функции различны).
Обозначается 
, например, 
, так как значения функций различаются при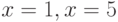 
и 
.
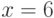Определение 7.4 Линейной называется булева функция аналитического вида
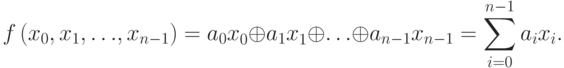
где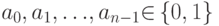 
-- произвольные значения 0 или 1. Множество всех линейных функций от переменных обозначим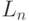 
.
Пример 7.2 Построим все линейные булевы функции от 2 переменных.
Для этого нам нужно перебрать все различные комбинации бит 
:
-
, или в векторном виде 
. -
, или в векторном виде 
, так как функция принимает значение 1 тогда и только тогда, когда младший бит аргумента равен 1, а это достигается при значениях аргумента 1 и 3 -- следовательно, в векторе на 0-й и 2-й позициях стоят 0, а на 1-й и 3-й -- 1. -
, или в векторном виде 
. -
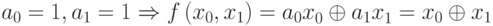, или в векторном виде 
- значение функции равно сумме по модулю 2 старшего и младшего битов аргумента.
Таким образом, множество линейных функций от 2 переменных:
Определение 7.5 Аффинной называется булева функция аналитического вида
где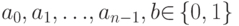 
-- произвольные значения 0 или 1. Множество всех аффинных функций от переменных обозначим 
.
Как нетрудно заметить, единственным отличием общего аналитического вида аффинных функций от линейных является наличие свободного члена 
, при этом если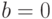 
, то функция является линейной, а при 
функция в векторном виде является побитовой инверсией соответствующей линейной в (при тех же значениях коэффициентов 
).
Таким образом, множество всех аффинных функций от переменных есть объединение множества всех линейных функций от переменных и множества их побитовых инверсий: 
.
Пример 7.3 Построим все аффинные булевы функции от 2 переменных.
Для этого нам нужно объединить уже построенное в примере 2 множество всех линейных булевых функций от 2 переменных с множеством их побитовых инверсий:
Нелинейностью булевой функции называется минимальное расстояние от этой функции до множества аффинных функций: 
.
Нелинейность показывает, насколько хорошо функция аппроксимируется линейными приближениями, другими словами, насколько хорошо можно подобрать такую линейную функцию, которая с большой вероятностью (при большом количестве различных значений входных переменных) будет давать то же значение, что и данная функция.
Пример 7.4 ([2]) Определим нелинейность функции 2 переменных 
.
Сначала необходимо построить множество всех аффинных функций от 2 переменных (мы это сделали в примере 3):
Теперь поочередно вычисляем расстояние от функции 
до каждой из функций этого множества и находим минимум:
Определение 7.6 Динамическим расстоянием 
-го порядка булевой функции 
называется число, вычисляемое по формуле:
Динамическое расстояние характеризует степень соответствия функции критерию лавинного эффекта, который заключается в том, что при изменении бит на входе выходное значение функции должно меняться с вероятностью 
. Порядок динамического расстояния характеризует число одновременно изменяемых бит. При динамическом расстоянии -го порядка, равном 0, говорят, что функция удовлетворяет строгому критерию лавинного эффекта -го порядка, что означает следующее: при одновременном инвертировании любых бит на входе функции ее значение инвертируется с вероятностью ровно .
Пример 7.5 ([2]) Определим динамическое расстояние 1 и 2 порядка функции 2 переменных .
Разберемся с нашим определением. Вектор 
-- это двоичный вектор длиной , причем такой, что его вес не превышает порядка определяемого динамического расстояния.
Таким образом, для нашей функции 2 переменных при определении динамического расстояния порядка 1 вектор может принимать 2 значения: 
и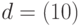 
.
Заметим также, что в сумме в формуле динамического расстояния суммирование ведется по всем возможным значениям аргумента функции 
-- двоичного вектора длиной .
Теперь вычисляем динамическое расстояние по формуле:
Чтобы теперь определить динамическое расстояние этой функции 2-го порядка, необходимо еще раз вычислить значение выражения, стоящего под знаком максимума, при 
-- так как максимальный вес вектора уже становится равным 2:
Таким образом, 
.
Определение 7.7 Блоком замен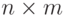 
бит называется отображение 
, то есть отображение, однозначно сопоставляющее любому входному вектору из бит выходной вектор из 
бит.
Нетрудно заметить, что блок замен есть не что иное, как набор из булевых функций, каждый из которых задает зависимость определенного бита на выходе блока от значений бит на входе. Любая процедура преобразования бит по определенному правилу может быть представлена в виде блока замен, если выписать все значения на выходе преобразования при всех возможных значениях на входе.
Способы задания блока замен:
1) Табличный -- в виде таблицы, каждая строка которой содержит значения выходных бит блока при определенном наборе значений входных бит. Число строк такой таблицы равно .
Пример 7.6 Таблица 7.3 задаёт блок замен 
.
|
|
|
 |
 |
 |
|---|---|---|---|---|---|
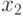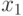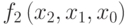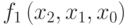| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
В данной таблице блок замен задан путем определения табличным способом трех булевых функций от трех переменных, определяющих зависимость выходных бит блока от входных.
2) Векторный -- в виде вектора, состоящего из значений блока замен, представленных в виде десятичного -битного числа, расположенных в порядке возрастания соответствующих значений аргумента, если их представить в виде в виде числа от 0 до 
(аналогично тому, как это делается при записи булевой функции в векторной форме).
Так, блок замен 
из примера 7.6 в векторной форме будет записываться следующим образом: 
(3-битовые значения на выходе блока представлены в виде целых чисел и выписаны сверзу вниз).
3) Аналитический -- в виде аналитически записанной зависимости выходных бит блока от входных. Например, в аналитической форме 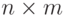битный блок замены путем целочисленного сложения с числом 
по модулю 
можно записать следующим образом: 
.
Пусть -- блок замен 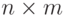бит, и 
-- булевы функции, выражающие зависимость соответствующих номерам функций выходных бит блока от входных. Иначе говоря, это столбцы правой части таблицы при записи блока замен в табличной форме (см.
рис.
7.4). Тогда нелинейность блока замен есть минимальная нелинейность всех возможных нетривиальных линейных комбинаций функций :
где 
.
Например, нелинейность блока из примера 7.6 будет рассчитываться следующим образом:
\textit{Нелинейность битового блока замен есть важнейшая его характеристика с точки зрения криптостойкости блока: она показывает степень устойчивости внутренней структуры блока к линейному методу криптоанализа. Следовательно, для достижения устойчивости шифрования к линейному криптоанализу необходимо, чтобы процедуры преобразования бит в ходе шифрования обладали как можно большей нелинейностью.}
Определение 7.8 Динамическое расстояние блока замен порядка 
определяется следующим образом:
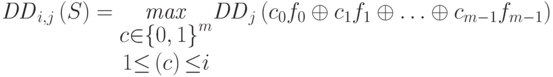
Таким образом, динамическое расстояние блока порядка есть максимальное динамическое расстояние порядка всех нетривиальных линейных комбинаций не более чем из 
функций из набора .
Смысл порядка динамического расстояния блока замен состоит в следующем: динамическое расстояние порядка 
характеризует степень отклонения вероятности изменения любого числа битов, не превышающего , на выходе блока от значения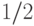 
при одновременном инвертировании не более битов на входе. Если динамическое расстояние блока замен порядка 
равно 0, то это означает, что при одновременном изменении не более битов на входе блока любой набор из не более чем бит на выходе одновременно изменится с вероятностью ровно .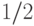
Например, динамическое расстояние порядка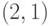 
блока из примера 7.6 будет рассчитываться следующим образом:
А динамическое расстояния порядка 
рассчитывается так:
Таким образом, динамическое расстояние блока замен есть вторая важнейшая его характеристика с точки зрения криптостойкости: она показывает степень устойчивости внутренней структуры блока к дифференциальному методу криптоанализа. Следовательно, для достижения устойчивости шифрования к дифференциальному криптоанализу необходимо, чтобы процедуры преобразования бит в ходе шифрования обладали как можно меньшим динамическим расстоянием как можно большего порядка.
