НОУ ИНТУИТ | Криптографические методы защиты информации. Лекция 2: Алгоритмы тестирования на простоту и факторизации

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 02.03.2017 | Доступ: свободный | Студентов: 2513 / 558 | Длительность: 21:50:00

Специальности: Программист, Администратор информационных систем, Специалист по безопасности, Архитектор программного обеспечения, Разработчик интернет-проектов

|

Вам нравится? Нравится 55 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

2.3 Компьютерные вычисления с большими числами

Как мы увидим в третьей главе, трудноразрешимые задачи, на которых основаны современные системы защиты информации, являются трудноразрешимыми только при использовании действительно больших чисел - размером в тысячи двоичных знаков. В данном параграфе мы рассмотрим некоторые инструменты программиста, полезные для работы с такими числами.

2.3.1 Калькулятор для больших чисел

При отладке любой программы, работающей с большими числами, часто приходится проводить какие-либо вычисления вручную, сравнивая их с результатами программы, и в этом помог бы калькулятор, работающий с большими числами. Стандартный калькулятор Windows непригоден для этих целей.

Играть роль калькулятора для больших чисел хорошо могут системы компьютерной алгебры. Помимо коммерческих систем, таких как Maple или Mathematica, существуют системы компьютерной алгебры с открытым исходным кодом, вполне подходящие для наших целей. Рассмотрим в качестве примера систему компьютерной алгебры Maxima, которую в виде дистрибутива для Windows, либо в виде исходных кодов можно загрузить с её официального сайта http://maxima.sourceforge.net/.

Maxima может работать как интерактивная среда командной строки, в режиме тетради (отличается от предыдущего тем, что введённые ранее команды можно поправлять и запускать заново) так и в виде неинтерактивного интерпретатора языка программирования Maxima, являющегося надстройкой над языком Lisp.

В качестве примера рассмотрим работу с Maxima в режиме тетради. После установки Maxima такой режим доступен из-под любой из двух графических оболочек Maxima: wxmaxima и xmaxima. На рисунке рис. 2.1 показан пример сеанса в графической среде wxmaxima.

увеличить изображение
Рис. 2.1. Снимок экрана сеанса работы в WxMaxima

В строках %i9, %i22, и т.д. пользователь вводил команду и по нажатии Shift+Enter получал ответ в соответствующих строках %o9, %o22, ...

Отметим лишь некоторые полезные для нас команды. Их подробное описание можно найти в поставляемой с maxima документцией.

\verb|chinese| - решение системы уравнений с помощью китайской теоремы об остатках.
\verb|igcdex| - расширенный алгоритм Евклида.
\verb|inv_mod| - нахождение числа, обратного к заданному числу по модулю.
\verb|jacobi| - символ Якоби.
\verb|lcm| - наименьшее общее кратное чисел.
\verb|power_mod| - возведение в степень по модулю.
\verb|primep| - тестирование числа на простоту с помощью теста Рабина-Миллера и Лукаса.
\verb|zn_log| - дискретное логарифмирование, использующее алгоритм Полига-Хеллмана и Ро-алгоритм Полларда.
\verb|zn_order| - вычисление мультипликативного порядка числа по модулю.
\verb|zn_primroot| - нахождение примитивного корня по модулю.

2.3.2 Программирование с большими числами в C/C++

При написании сложных систем защиты информации не обойтись без компилируемого языка программирования высокого уровня, например, C++. Стандартный тип целых чисел в C/C++ позволяет работать с числами не более 64 двоичных знаков, чего мало для криптографических приложений. Существуют библиотеки для C/C++, реализующие операции с большими числами и другие полезные криптографические функции. Отметим лишь некоторые из них, предоставляемые бесплатно с открытым исходным кодом:

openssl - библиотека, реализующая криптографический протокол SSL. В библиотеке реализованы операции и многие алгоритмы работы с большими числами, с ними и все реальные криптографические алгоритмы, рассматриваемые в данном пособии. В силу участившихся случаев обнаружения уязвимостей в openssl, в том числе, возможно, умышленно внесённых спецслужбами отдельных стран, был создан отдельный проект libressl, ставящий своей целью провести аудит исходных кодов и создать более отлаженную и выверенную версию библиотеки SSL. Написана на языке C, поэтому при программировании привычные формулы, например, x = y + z, пишутся в процедурном стиле:
```
BN_add(x, y, z);
     
```
GMP (GNU Multiple Precision) - библиотека, реализующая операции как с целыми числами больших размеров, так и с числами с плавающей точкой высокой точности. Не реализует никаких криптографических алгоритмов.
Crypto++ - криптографическая библиотека с интерфейсом на языке C++. В ней реализованы большинство популярных криптографических алгоритмов (российские стандарты блочного шифрования, цифровой подписи и хэш-функции не попали в их число). В качестве преимущества можно отметить перегрузку стандартных операторов, что позволяет переводить программы, уже написанные на C++ с использованием типов int, простой заменой типов int на CryptoPP::Integer.

Рассмотрим настройку окружения программиста для использования библиотеки Cryptopp.

Пример 2.3 Написать программу, принимающую два целых положительных числа A и B и вычисляющую символ Якоби $\left(\dfrac{A}{B}\right)$ .

Решение.

а) С помощью среды программирования Visual Studio 2010

Для Visual Studio придётся собирать библиотеку Cryptopp из исходных кодов, доступных на официальном сайте: http://www.cryptopp.com/.

После распаковки архива с исходными кодами нужно открыть и собрать решение cryptest.sln.

Нам понадобятся следующие файлы:

cryptopp.dll - динамически подгружаемая библиотека cryptopp. Библиотека содержит все функции cryptopp, и может быть подгружена нашей программой для их использования.
cryptopp.lib - библиотека импорта. Она содержит информацию, необходимую для присоединения cryptopp.dll к нашей программе. Файлы dll и lib можно найти в директории сборки решения cryptest.sln.
Все заголовочные файлы, входящие в архив с исходными кодами.

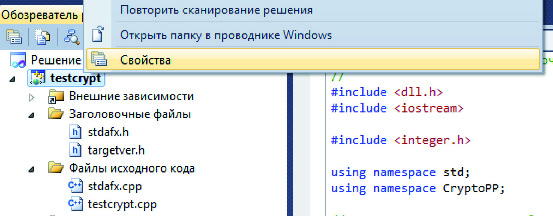
Создадим в Visual Studio 2010 проект "Win32 Console Application". Для того, чтобы в нашей программе использовать cryptopp, необходимо зайти в свойства нашего проекта (см. рис. 2.2)

Рис. 2.2. Для подключения cryptopp в Visual Studio необходимо зайти в свойства проекта

и указать

Путь к заголовочным файлам, содержащимся в архиве с исходными кодами cryptopp (Свойства конфигурации $\rightarrow$ C/C++ $\rightarrow$ Общие $\rightarrow$ Дополнительные каталоги включаемых файлов).
Путь к cryptopp.lib (Свойства конфигурации $\rightarrow$ Компоновщик $\rightarrow$ Общие $\rightarrow$ Дополнительные каталоги библиотек).
Свойства конфигурации $\rightarrow$ Компоновщик $\rightarrow$ Дополнительные зависимости - сюда необходимо добавить библиотеку импорта cryptopp.lib (не .dll!).

Файл cryptopp.dll необходимо скопировать в папку, в которой будет размещаться исполняемый файл нашей программы.

Теперь можно собрать решение с нашим проектом и проверить, что всё сделано правильно. Можно приступать к написанию исходного кода.

Код нашего проекта будет выглядеть следующим образом:

#include <dll.h>   //Этот файл должен быть включен до всех 
                   //остальных заголовочных файлов библиотеки
#include <iostream>//Модуль ввода/вывода стандартной библиотеки
                   //C++

#include <integer.h>//В этом заголовочном файле определяется 
                    //класс Integer больших чисел

using namespace std;
using namespace CryptoPP;//Все функции cryptopp находятся в 
                         //пространстве имен CryptoPP

//Функция, вычисляющая символ Якоби
int JacobiSymbol(Integer A, Integer P)
{
  //В самом начале P > 2 и нечетно (проверяется в main())
  int result = 1;
  while (true)
  {
    //Статический метод Gcd класса Integer вычисляет наибольший 
    //общий делитель; если он не равен единице, то символ Якоби
    //будет равен нулю (легко следует из определения)
    if (Integer::Gcd(A, P) > 1)
      return 0;
    
    //Теперь P > 1, НОД(A, P) = 1

    //Равные по модулю P числа являются или не являются 
    //квадратичными вычетами одновременно
    if (A >= P)
      A = A % P; 
    
    //Теперь 1 < A < P, P > 1, НОД(A, P) = 1

    //Отделить четную часть числа A. Определим, на какую 
    //степень двойки делится число A, и символ Якоби 2 по P
    //найдём по свойству.
    int pwr_ = 0;
    while (A.GetBit(pwr_) == false)
      pwr_++;
    if (pwr_ >0)
    {
      A>>=pwr_; //Поделить A на степень двойки
      int pwroftwo = pwr_%2;
      if (pwroftwo == 1)
        if ((P*P-1)%16 != 0)
          result *= -1;
      continue;
    }
    
    //Теперь A нечетно, P > 1, A < P, НОД(A, P) = 1
    if (A == 1)
      break;

    //Теперь A, P нечетны, больше 1 и взаимно просты. Поэтому
    //можно применить квадратичный закон взаимности. 
    if (((A - 1) * (P - 1))%8 != 0)
      result *= -1;
    A.swap(P);
    
    //Теперь снова P > 1 и нечетно, поэтому можно
    //возвращаться в начало цикла.
  }
  return result;

}

int main(int argc, char** argv)
{
  if (argc==3)
  {
    //Проверить корректность аргументов командной строки
    bool correctnumbers = true;
    for (int j=1; j<=2; j++)
      for (int i=0; argv[j][i]!='\0'; i++)
        if ((argv[j][i]<'0') || (argv[j][i]>'9'))
          correctnumbers = false;
    //Если аргументы корректны, посчитать их символ Якоби
    if (correctnumbers == true)
    {
      Integer a(argv[1]);
      Integer b(argv[2]);
      if (b<3)
        cout<<"Jacobi symbol (a/b) is not defined for b="
        <<b<<endl;
      else
      {
        cout<<JacobiSymbol(a,b)<<endl;
        return 0;
      }
    }
  }
  cout<<"Expected two positive integer numbers"<<endl;
  return -1;
}
\end{verbatim}

После сборки программу нужно запускать из консоли. Например:

\verb|testcrypt.exe 51 343543|

Конечно, наша программа допускает вычисления и с куда большими числами.

Серьёзным минусом данного подхода является необходимость приобретать Microsoft Visual Studio для разработки под Windows. Не станем перечислять причины, по которым в бесплатной версии Microsoft Visual Studio Express описанные нами действия не приведут к успеху.

б) В операционных системах семейства linux

В операционных системах семейства linux огромное количество библиотек, доступных разработчику, запакованы в специальные архивы, называемые пакетами. Отличие пакета от архива в том, что между пакетами существуют зависимости, позволяющие программе установки автоматически устанавливать не только библиотеку или программу, которую попросил пользователь, но и все требуемые для их работы дополнительные библиотеки. Обычно библиотека и заголовочные файлы к ней запаковываются в разные пакеты. Пакет с заголовочными файлами, как правило, имеет суффикс -dev или -devel.

В linux-системах, основанных на Debian GNU/Linux, для разработки с использованием cryptopp требуется установка всего двух пакетов. Все действия можно выполнить из коммандной строки с правами администратора:

# apt-get install libcrypto++-dev

Благодаря автоматической системе распознавания зависимостей также будет установлена нужная версия библиотеки libcrypto++.

Как и в Windows, в Linux доступно множество сред разработки. Действия, производимые в среде разработки Eclipse (с подключенным расширением CDT - C Development Tools), аналогичны нашим предыдущим действиям в Visual Studio.

Создать простой проект C++
Из панели Project Explorer открыть свойства проекта
C/C++ Build $\rightarrow$ Settings $\rightarrow$ Tool Settings $\rightarrow$ GCC C++ Compiler $\rightarrow$ Includes. В верхнем окне, Include paths, нужно добавить путь к заголовочным файлам (обычно, /usr/include/crypto++)
С/C++ Build $\rightarrow$ Settings $\rightarrow$ Tool Settings $\rightarrow$ GCC C++ Linker $\rightarrow$ Libraries. В верхнем окне, Libraries (-l), нужно добавить строку "crypto++".
Написать исходный код программы
Собрать проект
Запускать проект, передавая числа A и B через аргументы командной строки.

Недостаток проектов Eclipse (так же, как и Visual Studio) в том, что в них явно указывается путь к заголовочным файлам, которые на другом компьютере могут располагаться в другой директории. Поэтму рекомендуется создать файл проекта, не зависящий от среды разработки, например, проект в системе сборки Cmake (см. http://www.cmake.org/documentation/).

Для автоматического поиска заголовочных файлов и самой библиотеки используется система pkgconfig. Её можно использовать из cmake-проекта следующим образом.

Создадим файл jacobi.cpp с исходным кодом нашей программы
В той же директории создадим файл CMakeLists.txt со следующим содержимым:
```
cmake_minimum_required(VERSION 2.4)
project(jacobi)
INCLUDE(FindPkgConfig)
pkg_check_modules(CRYPTOPP REQUIRED libcrypto++)
include_directories(${CRYPTOPP_INCLUDEDIR} ${CRYPTOPP_INCLUDEDIR}/cryptopp)
link_directories(${CRYPTOPP_LIBRARY_DIRS})
add_executable(jacobi jacobi.cpp)
target_link_libraries(jacobi ${CRYPTOPP_LIBRARIES})
     
```
Здесь project(jacobi) указывает имя cmake-проекта; в следующих четырех строках мы указываем системе pkgconfig искать заголовочные файлы и библиотеку crypto++. В последних двух строках мы указываем, какой создавать исполняемый файл, и какие к нему подключить библиотеки.
Сборка cmake-проекта осуществляется командами:
```
\verb|cmake && make|
     
```

Для отладки программы, снабженной файлом Cmake-проекта, можно использовать интегрированные среды разработки. Одна из лучших сред разработки с поддержкой Cmake - QtCreator.

Список литературы

Черемушкин А.В. Арифметические основы криптографии - М.: МЦНМО, 2002. - 104 с.

Дальше >>

Авторизоваться

Криптографические методы защиты информации

Алгоритмы тестирования на простоту и факторизации

2.3 Компьютерные вычисления с большими числами

2.3.1 Калькулятор для больших чисел

2.3.2 Программирование с большими числами в C/C++

Список литературы

Вопросы и ответы