|
Куда нажать? Сумма на лс есть. Как можно получить распечатанный диплом ? |
Изменение вычислительно-информационной парадигмы: новые подходы и модели
11. Изменение вычислительно-информационной парадигмы: новые подходы и модели
Быстродействие современных вычислительных средств уже довольно близко подошло к теоретическому пределу. Этого быстродействия, однако, оказывается недостаточно для того, чтобы практически решать новые сложные задачи управления неоднородными нелинейными системами, осуществлять непрерывный анализ огромных потоков информации, реализовывать основные функции "искусственного интеллекта".
Поэтому все более становится актуальным, так называемый "новый" взгляд на информационные процессы. Этот взгляд, основывается на идее, что всё лучшее уже существует — и существует в природе! Выявление принципов работы существующих в природе механизмов обработки информации и внедрение этих результатов в технические системы является одним из приоритетных путей развития техники.
В природе есть сверхпроизводительный биологический параллельный компьютер с миллиардами нейронов-процессоров, глобально связанных друг с другом (до десятка тысяч связей у каждого) — головной мозг. И это несмотря на то, что "тактовая" частота работы отдельного элемента-процессора достаточно низкая. В связи с этим интересно проследить эволюцию идей реализации параллельных вычислений.
11.1. Эволюция вычислений и вычислительных устройств
За шесть десятилетий быстрого развития средств вычислительной техники пройден путь от ламп, через транзисторы, интегральные микросхемы к сверхбольшим интегральным микросхемам (рис. 11.1).
Что будет дальше? Основной вопрос настоящего времени уже не сводится просто к наращиванию мощности вычислительных устройств — он трансформировался к вопросу: "Как эффективно использовать имеющиеся мощности для сбора, обработки и использования данных?"
Быстрое развитие электронных технологий приводит к тому, что компьютеры становятся все меньше и меньше, что позволяет использовать их во всё более миниатюрных устройствах – мобильных телефонах, цифровых фотоаппаратах, различных видеустройствах. Когда-то думали, что более мощные вычислительные системы по необходимости будут требовать больше места под периферию, память и т.д. Это предположение оказалось неверным. В 1965 году. Г. Мур сформулировал правило, имеющее силу и сейчас ("закон Мура"), согласно которому производительность вычислительных систем удваивается каждые восемнадцать месяцев.
Мур вывел свой эмпирический закон, построив зависимость числа транзисторов в интегральной микросхеме от времени. Как следствие, из этого можно было оценить темпы миниатюризации отдельного транзистора. В настоящее время развитие цифровых технологий приводит к тому, что размер элементарного вычислительного устройства приближается к размеру молекулы или даже атома. На таком уровне законы классической физики перестают работать и начинают действовать квантовые законы, которые для многих важных динамических задач еще не описаны теоретически.
Увеличение быстродействия вычислительных устройств и уменьшение их размеров с неизбежностью приводит к необходимости операций с "переходными" процессами. Логично было бы перейти от устоявшихся операций с классическими битами к операциям, задаваемым теми или иными динамическими моделями микромира. Введение более широкого класса моделей было бы более обоснованным, если бы удалось, например, для функции, значения которой записаны в кластере квантовых битов, определить операцию, эффективно выполняющую, например, преобразование Фурье. При этом вполне может оказаться, что время на её выполнение будет соизмеримым со временем выполнения одной классической операции, так как аналоги операций типа операции "свертки функций" вполне могут обнаружиться "в природе". Исследования похожих моделей, проводившихся в последнее время, показывают, что их выполнение за счет присущей природе способности к самоорганизации не обязательно "раскладывается" на более простые кирпичики, т.е. не всегда может быть записано в виде классического алгоритма
Новые потребности, глобализация задач, экспоненциальное возрастание сложности вычислительных систем и наметившаяся в последнее время подъём отечественной ИТ-отрасли в развитии суперкомпьютерных вычислений (суперкомпьютеры российских компаний "T-Платформы", "СКИФ-Аврора", появление суперкомпьютера "Ломоносов" в Московском государственном университете и другие проекты) заставляют уже в практическом плане задуматься о перспективах и возможной смене парадигмы: "Каким должен быть процесс вычислений?" Объективные сегодняшние тенденции — миниатюризация и повышение производительности процессоров, как это и было предсказано законом Мура — приводят технологии к порогу развития традиционных вычислительных устройств. От приоритетов бесконечного наращивания тактовой частоты и мощности одного процессора производители переходят к многоядерности, параллелизму и т. п.
На прошедшей в сентябре 2012 года в Абрау-Дюрсо Международной научной конференции "Научный сервис в сети Интернет: поиск новых решений" во многих докладах ставился вопрос: "Что будет при переходе от сегодняшних производительностей суперкомпьютеров в "TeraFlops" к следующему масштабу "ExaFlops"? В этой связи один из организаторов конференции, член-корреспондент РАН Вл. В. Воеводин говорил: "Переход к "ExaScale", естественно, должен будет затронуть такие важнейшие аспекты вычислительных процессов, как: модели программирования, степень и уровни параллельности, неоднородность программных и аппаратных систем, сложность иерархии памяти и трудности одновременного доступа к ней в распределенных вычислениях, стек системного и прикладного ПО, надежность, энергопотребление, сверхпараллельный ввод/вывод … " .
Анализ развития вычислительной техники показывает, что, несмотря на проявление спиральной тенденции, присутствует еще и параллельная эволюция идей о мультипроцессорности или о многоэлементности при реализации вычислений. Можно отметить, что одновременно с развитием различных параллельных архитектур на базе "простых" процессорных элементов (от матричных, систолических и транспьютерных к кластерным архитектурам) успешно реализована идея многоядерных процессоров и усложнения отдельного вычислительного элемента — процессора. В последнее время эта тенденция продолжает развиваться.
Сейчас несколько ядер в процессоре переносного компьютера — уже норма, а в процессорах суперкомпьютеров ядер в тысячи раз больше. "Джин выпущен из бутылки": пройдет совсем немного времени и ядер станет несколько десятков, а потом и сотен тысяч!
Появятся совершенно другие архитектуры, ядра будут объединяться в сложные композитные блоки. К данным можно будет получать одновременный параллельный доступ разным вычислительным блокам, "общение" вычислительных блоков между собой будет происходить через общую память.
Всё это приведет к тому, что изменятся многие аспекты парадигмы: "Что такое вычислительное устройство и что такое вычислительный процесс". Изменятся традиционные представления о том, как устроен компьютер, что такое вычислительная система. Эти процессы принесут изменения и в стиль программирования, и в то, как будут использоваться вычислительные устройства и готовиться данные для вычислений. По нашему мнению, всё это неизбежно приведёт к смене парадигмы высокопроизводительных вычислений (рис. 11.2)!
Переход к новой парадигме вычислений и обработке информации приведет, видимо, к тому, что архитектура вычислительных устройств "сдвинется" в сторону "набора одновременно работающих асинхронных моделей взаимодействующих динамических систем (функциональных элементов)". Среди новых характерных параметров будущей парадигмы все более отчетливо проступают следующие: стохастичность, гибридность, асинхронность, кластерность (отсутствие жесткой централизации и динамическая кластеризация на классы связанных моделей).
Стохастичность. С одной стороны, хорошо известно, что компьютеры становятся все миниатюрнее и миниатюрнее, размер элементарного вычислительного элемента (вентиля) приближается к размеру молекулы или даже атома. На таком уровне законы классической физики, как было сказано выше, перестают работать, и начинают действовать квантовые законы, которые в силу принципа неопределенности Гейзенберга принципиально не дают точных ответов о состоянии элемента вычислительной системы. С другой стороны, стохастичность — это известное свойство сложных динамических систем, состоящих из огромного числа компонент.
Под гибридностью будущих процессов вычислений можно понимать необходимость рассмотрения комбинации непрерывных и дискретных процессов, т. е. учет непрерывной эволюции протекания физических процессов при работе той или иной модели и скачкообразное переключение с одной модели на другую.
Увеличение быстродействия вычислительных устройств и уменьшение их размеров с неизбежностью приводит к необходимости операций с "переходными" процессами. Серьёзным ограничением классической модели вычислений является разбиение памяти на изолированные биты. Во-первых, сокращение длины такта и расстояний между битами с определенного уровня делает невозможным рассматривать их изолированно в силу законов квантовой механики. Вместо примитивных операций с классическими битами в будущем логично перейти к операциям, задаваемыми теми или иными динамическими моделями микромира, оперирующими с наборами взаимосвязанных "битов". При этом простейшими "моделями" могут остаться классические операции с битами.
Асинхронность. Отказ от унифицированных простых вычислительных элементов неизбежно приводит к отказу от синхронизации работы различных компонент, имеющих существенно отличающиеся физические характеристики и свои длительности "тактов". В рамках классической теории множеств противоречивый смысл понятия единого "такта" выражается в рамках неразрешимости проблемы континуума в рамках аксиоматики Френкеля-Цермело.
Кластерность. Одним из неожиданных результатов многочисленных попыток в разработках (создании, адекватном описании поведения и управлении) сложных стохастических систем оказалась перспективность модели мультиагентных систем, в которой топология связей агентов между собой меняется со временем. При этом "агентом" может быть как некоторая динамическая модель (компонент системы), так и определенный набор моделей. При отсутствии жесткой централизации такие системы способны эффективно решать достаточно сложные задачи, разбивая их на части и автономно перераспределяя ресурсы на "нижнем" уровне, а эффективность часто повышается за счет самоорганизации агентов и динамической кластеризации на классы связанных моделей.
В некотором смысле, переход к разработке и созданию моделей сложных вычислений закономерный этап развития микропрограммирования. Понимание возможных преимуществ работы устройств с эффективным микрокодом отмечалось еще в 50-е годы прошлого века. В настоящее время технологии микропрограммирования, т.е. создания программ в виде компилируемых текстов, естественным образом сдвигаются в сторону физических процессов.
В тоже время все большее распространение получают нейронные системы и нейрокомпьютеры, которые являются параллельными вычислительными устройствами по определению. В концепции облачных вычислений также присутствует идея распараллеливания вычислений. Таким образом, одновременно идет развитие структур, состоящих из большого количества относительно сложных элементов и наращивание их числа, с другой стороны — усложнение отдельного элемента (многоядерные структуры), и развитие идей параллельных вычислений на множестве сложных автономных вычислителей. Эти вычислители соединены сетью заданной структуры, реализованной для решения определенного класса сложнейших задач — как теоретических (математика, механика, физика, лингвистика), так и прикладных (биология, химия, медицина, геофизика и метеорология, экономика и многие другие области знания).
Сложность использования многоядерных, многопроцессорных и кластерных структур заключается в необходимости использования специальных средств программирования, так как изначально программы не являются параллельным представлением алгоритмов решения задач. Это приводит, например, к тому, что зачастую второе, третье (и так далее) ядро процессора у пользователя, не являющегося профессиональным программистом, не задействуется. Наличие специализированных языков параллельного программирования, выбор которых зависит от используемой платформы, также затрудняет эффективное использование многопроцессорных и многомашинных комплексов. Появление стандарта параллельного программирования несколько улучшило ситуацию, но не существенно.
В этой связи достаточно убедительными оказываются доводы о том, что архитектура нейросетевых систем изначально адекватна параллельному представлению решаемой задаче и более естественна для высокопроизводительных вычислений. Можно это охарактеризовать как конвергенцию идей — движение навстречу друг другу разных подходов. С одной стороны — усложнения отдельного элемента системы (как в нейронных сетях) и с другой стороны — увеличение числа процессоров с одновременным изменением их структуры. Это говорит о том, что в дальнейшем для решения действительно сложных задач будет найдено компромиссное решение: "сложный элемент — простая структура" и/или "сложная структура – простой элемент". Видимо, эффективное решение лежит между этими двумя крайними проявлениями и может быть охарактеризовано как "относительно сложный элемент и относительно сложная структура". При этом степень относительности и сложности будут зависеть от конкретного класса решаемых задач.
11.2. Нелинейная динамика и синергетика – возможности применения в параллельных вычислениях
Одно из наиболее перспективных направлений поиска высокопроизводительного интеллектуального вычислительного устройства лежит в области моделирования работы человеческого мозга. Из результатов исследования электрической активности мозга нейрофизиологами следует, что мозг является нелинейной динамической системой с хаотической природой электрохимических сигналов. Сложная структура коры головного мозга моделируется с помощью взаимосвязанных нейронных решеток. Глобальная связь между нейронами порождает их коллективное поведение. Каждый нейрон представляет собой отдельное устройство, которое можно сопоставить процессору вычислителя. Именно поэтому структура нейронной сети наиболее подходит для выполнения параллельных вычислений, поскольку нет необходимости в предварительной подготовке исходных данных перед распараллеливанием.
Десятки сотен проектов, направленных на исследование принципов функционирования головного мозга человека, также способствовали становлению новой предметной области — нелинейной динамики. Нелинейная динамика — это часть синергетики, которая изучает коллективное поведение множества нелинейных объектов: квантов, атомов, молекул, клеток (в частности нейронов), подсистем. Одним из направлений в нелинейной динамике является изучение проявления самоорганизации в синхронизации хаотических систем. Изучение синхронизации — этого фундаментального явления природы — проводится в биохимии, биофизике, квантовой физике, нейропсихологии, нейрофизиологии, нейробиологии.
Отметим, что исследования все более приобретают междисциплинарный характер. Поскольку всё связано со всем, то закономерности, которые выявляются в поведении и функционировании элементов одной природы, иногда могут быть использованы для управления элементами другой природы. Как показывают многочисленные исследования в области нелинейной динамики — чем сложнее задача, тем сложнее динамика системы, и, следовательно, управление ею. Поэтому все больше работ посвящено объединению достижений в области нелинейной динамики, самоорганизации и теории нейронных сетей.
При разработке новых высокопроизводительных систем на основе принципов самоорганизации предполагается, что решение задачи и соответствующая структура для ее решения самоорганизуются за счет внутренних процессов в системе и за счет обратной связи с внешней средой — классических задач низкоуровневой функциональной декомпозиции в данном случае не возникает. Более того, использование синергетического синтеза также предполагает отсутствие классического разделения в вычислениях на аппаратную и программную части.
Такое вычислительное устройство, как было сказано выше, может представлять собой набор асинхронных моделей динамических систем, взаимодействующих между собой и сочетающих такие свойства, как гибридность, асинхронность, кластерность, стохастичность.
О. Н. Граничин и его соавторы предложили и обосновали новую абстракцию вычислительного устройства, обобщающую схему классической машины Тьюринга. В рамках новой модели переосмысливаются ставшие традиционными понятия "такт", "память", "ленты", "программы" и "состояния".
Если в классическом подходе ячейки памяти используются для хранения дискретной информации и их изменение возможно только в тех случаях, когда указатель ленты показывает на нее, то в новой концепции "ячейка памяти" представляет собой постоянно функционирующую модель достаточно сложной динамической системы, а "лента" — подмножество в общем пространстве состояний, при достижении которого заканчивается очередной "такт" и происходит включение "программы" — скачкообразное переключение с одних моделей на другие. Естественно, что классическая ячейка памяти для хранения единицы информации ("бита") является частным случаем такого обобщения.
В любых современных вычислительных устройствах хранение информации основано на тех или иных физических принципах, только эволюция состояния ячейки во время хранения более простая — сохраняется постоянной какая-то физическая характеристика. Другими словами, поле вычислений в традиционной информатике можно сравнить с арифметикой, она оперирует цифрами — значениями ячеек памяти (или, более точно — арифметикой конечных двоичных дробей). Предлагаемая новая модель вычислений позволит перейти в информатике от "арифметики" к "функциональному анализу", исследующему процессы эволюции информации внутри новых "ячеек" (операции с функциями).
Другим обобщением может быть вероятностное задание отображений эволюции и программ, что позволит реализовывать с помощью новой модели динамические системы, стохастические гибридные системы, вероятностные автоматы, системы со стохастическим управлением, то есть системы, не описываемые детерминированными законами. Для организации работы такой вычислительной системы, наверное, целесообразно будет использовать рандомизацию, позволяющую частично устранить влияние на работу системы систематических погрешностей, которые практически неизбежны при изменяющейся со временем модели динамической системы.
Предлагаемая новая модель вычислений позволяет описывать если не все, то подавляющее большинство процессов реального мира, а также работу всевозможных существующих и будущих вычислительных устройств, включая аналоговые и биокомпьютеры, нейрокомпьютеры, квантовые компьютеры и т. д. Особенностью рассматриваемого подхода является отказ от редукции сложности в процессе вычисления. Сложность вычислимого объекта должна быть эквивалентна сложности вычисляемого.
Другими словами, понятие вычислительной сложности правильнее рассматривать относительно выбранной системы базисных эволюционных примитивов, а не относительно традиционно рассматриваемых битовых преобразований 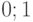 . Квантовые и нейрокомпьютеры обещают сильно изменить представления о вычислительной мощности современных вычислительных устройств. Увеличение вычислительной мощности, возможное за счет использования новых моделей вычислений, основывающихся на физических явлениях, позволяет предположить, что в будущем новые компьютеры смогут решать задачи, невыполнимые для обычных компьютеров.
. Квантовые и нейрокомпьютеры обещают сильно изменить представления о вычислительной мощности современных вычислительных устройств. Увеличение вычислительной мощности, возможное за счет использования новых моделей вычислений, основывающихся на физических явлениях, позволяет предположить, что в будущем новые компьютеры смогут решать задачи, невыполнимые для обычных компьютеров.
Модель вычислений для такого устройства можно свести к совокупности следующих базовых параметров:
- набор вычислительных примитивов (динамические модели
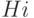 с параметрами
с параметрами  );
); - память
 — общее пространство состояний всех моделей;
— общее пространство состояний всех моделей; - лента
 — динамический граф с конечной битовой строкой
— динамический граф с конечной битовой строкой  "включения" моделей в узлах;
"включения" моделей в узлах; - программа
 — заданные на графе
— заданные на графе  правила (или цели) переключения "ленты" и параметров моделей при попадании пары
правила (или цели) переключения "ленты" и параметров моделей при попадании пары 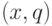 на одном из "включенных" узлов в множество переключения
на одном из "включенных" узлов в множество переключения 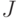 ;
; - такт — промежуток времени между соседними моментами переключений;
- множество останова
 .
.
В этом случае уместно говорить об обобщенной машине Тьюринга, которую можно представить в виде кортежа взаимосвязанных компонентов 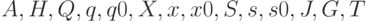 , где
, где  — множество моделей (вычислительных примитивов),
— множество моделей (вычислительных примитивов),  — оператор эволюции,
— оператор эволюции,  — множество состояний (значений параметров),
— множество состояний (значений параметров),  — память,
— память,  — обобщенная лента (граф),
— обобщенная лента (граф), 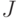 — множество переключений,
— множество переключений,  — программа (цели),
— программа (цели),  — множество останова.
— множество останова.
Здесь можно также отметить взаимное сближение технологий разработки программного и аппаратного обеспечения. Это связано с широким распространением программируемых архитектур, в которых, тоже используется большое число относительно простых ячеек, которые программируется под определенные функции путем определенного связывания друг с другом. В связи с этим получили развитие языки аппаратного программирования, процедуры отладки и среды разработки как в программном обеспечении. Программирование, отладка тестирование при разработке аппаратуры оказываются очень схожими с разработкой программных комплексов.
Еще одно из активно развиваемых и используемых решений для высокопроизводительных вычислений — платы компьютерной графики, содержащие огромное число не слишком сложных графических процессоров-вычислителей. Первоначально такие процессоры были предназначены для ускорения работы приложений компьютерной графики, у которой задачи принципиально параллельны и требуют одновременной обработки всех компонент графической картинки. Однако эти структуры оказались очень эффективным средством для решения задач вычислительной физики и параллельного проведения экспериментов и для нейровычислений. Правда надо отметить, что для использования возможностей графических ускорителей также необходимо знание и использование специального языка обращений к матрице графических процессоров. Но так как логический базис операций этих процессоров естественным образом оказался совместим с требуемыми операциями при проведении нейровычислений и других параллельно представленных задач, то этот подход использования графических ускорителей, при условии дальнейшего совершенствования средств их программирования, будет получать все большее и большее распространение.
Кроме того, существует такая тенденция, как придание аппаратной реализации большей гибкости — разработка процессоров и многопроцессорных архитектур с переменной структурой. И здесь также есть решения на уровне переменной организации отдельного элемента, так и для всей структуры из большого числа элементов. Это согласуется с теми тенденциями, которые можно наблюдать в развитии идей нейровычислений. В нейронных сетях структура нейронной сети адаптируется под решаемую задачу как в малом — на уровне отдельных весовых коэффициентов в пределах заданной структуры, так и в большом — при отсутствии ограничений на композицию нейронных ансамблей.
Вместо привычного представления исходной задачи, подлежащей решению в виде совокупности функций, для последующей реализации, или разделении системы на отдельные части, при синергетическом походе проводится синтез и исследование системы как единого целого. Изменение состояния отдельного элемента системы может никак не повлиять на состояние системы в целом, однако, совместная динамика всех элементов определяет макроскопическое уникальное состояние системы. И это состояние системы и будет являться решением поставленной задачи.
Именно возникновение синхронизации, коллективного поведения позволяет живым системам адаптироваться, обучаться, извлекать информацию и в реальном времени решать вычислительно сложные задачи за счет распределенной обработки информации. Много элементов со сложной динамикой порождают эффективные вычисления.
11.3. Искусственный интеллект
Человечество накопило большой массив задач, которые компьютеры умеют эффективно решать. Можно рассчитать параметры ядерного взрыва, можно построить модель космологического расширения Вселенной, можно быстро найти решение какого-нибудь важного уравнения, составить долгосрочный экономический прогноз и многое-многое другое. При этом одних задач достаточно настольного компьютера, для решения других — требуется мощный суперкомпьютер. Но как нам поступить, если мы хотим "собрать" универсальный вычислитель, который способен один решать задачи разных уровней сложности?
Предположим, что мы делаем не вычислитель, быстро решающий уравнения — наша цель создать "искусственное мыслящее существо", которое в условиях неопределенностей способно распознать реальную ситуацию, выбрать адекватную ей задачу и решить ее. Например, среди всего реализованного набора задач компьютер сам принимает решение о выборе блока, ответственного за решение определенной задачи, который отвечает на запрос: "Да, я распознаю ситуацию, я контролирую её, это моя цель, с ней следует поступать так или этак в зависимости от развития ситуации и т. п.".
Такие системы, которые работают в ситуациях, описываемых в терминах нечеткой логики, плохо "вписываются" в традиционную концепцию архитектуры компьютера, в которой операции обычно выполняются последовательно, данные загружаются последовательно, для выполнении того или иного действия надо последовательно пройти некоторые шаги А, Б, В, …, задаваемые алгоритмом решения. При достаточно большом количестве шагов и громадных объемах данных, зачастую решаемая задача перестает быть актуальной.
Что можно ждать в перспективе? Простое решение, по которому сейчас идут практически все разработчики вычислительных систем — собрать всевозможные вычислительные блоки вместе и наращивать их вычислительную мощность — в сегодняшних условиях уже наталкивается на серьёзные проблемы. Это одновременная доставка и структуризация огромных объёмов информации, выбор "ведущего" блока, синхронизация работы многоядерных систем, оптимизация энергетических затрат на производство вычислений, отвод тепла от процессорных блоков и многие другие проблемы.
Наверное, когда-то мы сможем собрать блоки (микросхемы), решающие выбранные нами задачи (желательно все), в "клубок" закрученной спирали, как в молекулах ДНК в клетках биологического организма (рис. 11.3), которые одновременно решают огромное количество задач (аналоги вычислительных функций).
Как могут решаться важные для универсального вычислителя задачи с доступом к памяти, с параллелизмом, данными? Гипотетически можно представить, что химическое или электромагнитное воздействие (например, луч света или другой вид излучения) на такой "клубок" может одновременно воздействовать сразу на все блоки, и каждый из них одновременно с другими "примеряет" поступающую информацию "на себя". Традиционная альтернатива параллелизму — перебирать блоки по очереди и смотреть, кому и что лучше подходит. В том блоке, который распознал адекватность текущей информации его задаче и которому информация "подошла" лучше остальных, можно сопоставить возникновение состояния некоторого информационного резонанса.
Рассмотрим пример интеллектуальной системы, работающей на перечисленных выше принципах. Представим себе робота, взаимодействующего с реальным миром через стандартные устройства — датчики, видео и фотокамеры, микрофоны, радиолокаторы, сервомеханизмы. Центральный компьютер робота состоит из тысяч устройств (блоки из "моделей"), обрабатывающих наборы данных, поступающих из внешнего мира, и создающих внутреннее представление (отражение) реального мира в "мозгу" робота. Это представление по очевидным причинам будет создаваться с помехами и должно постоянно корректироваться.
Центральный компьютер использует созданное представление мира для расчета базисной стратегии и оптимальных траекторий перемещения, позволяющих избежать опасностей и выполнить поставленное задание. Функционирование робота в подобных условиях можно представить как одновременное выполнение совокупности параллельных задач, контролируемых разными устройствами в центральном компьютере. Следует отметить, что если резонансные устройства не конкурируют за общий ресурс (видеокамеру, исполнительное устройство и т. д.), то нет необходимости выбирать из них главное.
Работа всех устройств робота (в том числе и вычислительных) регулируется вектором параметров, размерность которого может быть очень большой. Поиск оптимальных значений этих параметров возможен только после постановки задачи, включающей в себя определение функционала качества. В этом случае функционал качества будет оцениваться центральным компьютером. Основные возможные критерии — соответствие внутренней картины мира реальным условиям (число коррекций), число и качество информационных резонансов и т. д. Настройку параметра с высокой размерностью удобнее всего производить рандомизированным алгоритмом стохастической оптимизации, который хорошо ложится на логику квантовых вычислительных устройств и по многим параметрам предпочтительнее других подобных алгоритмов для оптимизации систем в реальном времени.
Ещё один, более конкретный пример. Предположим, что у нас есть набор устройств, способных распознавать определенные виды изображений (каждое из устройств настроено на какой-либо конкретный объект). Все эти устройства получают в реальном времени изображение с некоторой цифровой камеры. В каждый момент времени только одно из устройств, объявившее себя "главным", может управлять камерой. Существует также одно устройство, управляющее камерой в случаях, когда никто не объявил себя главным. Оно может действовать по какому-нибудь простому алгоритму — например, осматриваться вкруговую или сканировать некоторый важный участок, в котором ожидается появление объектов. Картинка с камеры постоянно подается на входы всех распознавателей, и те в свою очередь пытаются распознать в ней свой объект.
Результатом их работы является степень совпадения в процентах (например, объект является движущимся животным или человеком с вероятностью 75%). Под информационным резонансом естественно понимать превышение "степени достоверности" у какого-то из устройств заранее установленного порога (например, 90%), в результате это устройство объявляет себя главным и берет на себя управление камерой для более детального изучения объекта или слежения за ним.
Резюмируя сказанное выше, можно заключить, что рост мощности "классических" вычислительных устройств и постоянное расширение классов научных и прикладных задач, усложнение этих задач, проблемы с вводом и обработкой данных в суперкомпьютерах с неизбежностью приведут к смене парадигмы вычислений. Из этого с неизбежностью следует необходимость поиска путей создания принципиально новых вычислительных систем, основанных на гибридных стохастических устройствах.
11.4. Практические задачи и устройства для их решения: "новый-старый" подход
Потребности решения все более сложных задач и в то же время широкие возможности, которые предоставляются в случае применения синергетических принципов анализа и синтеза, приводят к тому, что для комплексных сложных задач, в которых должны проявляться эмерджентные системные свойства, все более эффективным становится подход целостного анализа в едином комплексе без деления на части. Это не отход от функциональной декомпозиции, а существенное его дополнение, так как при разделении системы или задачи на части мы, зачастую, теряем уникальность, связанную с системными закономерностями.
С другой стороны, при использовании единого подхода появляется возможность естественного совмещения операций. Например, для информационных систем — это и восприятие, и хранение, и собственно обработка информации. От ассоциаций к хранению и последующему распознаванию, что согласуется с текущими представлениями о том, как решаются задачи живыми системами.
Таким образом, предлагается общий подход к решению разных задач, (почти как в нейроинформатике — "разнотипные к однотипному представлению"), сведение всего или к задаче управления или задаче оптимизации или задаче распознавания образов. Этот подход схож с нейросетевым в той части, что касается ведения разнотипных задач к однотипным и решаемым однородными сетевыми структурами. При таком подходе сложность метода (устройства) будет адекватна решаемой задаче также, как в формальной теорией синтеза структуры нейронной сети через функционалы первичной и вторичной оптимизации .
В связи с этим основное внимание уделяется развитию методов обработки информации и раскрытию их связи с законами функционирования объектов различной природы (физической, химической и др.), в которых также проявляется существование общего механизма упорядочивания, несмотря на присутствие хаоса в функционировании отдельных элементов системы. При этом за основу принимаются модели и результаты, полученные в физике кластеров и при исследовании осцилляторных и рекуррентных нейронных сетей, представляющих собой дискретные хаотические системы большой размерности.
На основе анализа взаимного соответствия между объектами различной природы, в которых существуют механизмы самоорганизации, и синтезируемой физико-технической системой вычислительного устройства предлагается разработать как математическое обеспечение нового адаптивного высокопроизводительного вычислителя, позволяющее определять состав и структуру вычислителя в зависимости от предъявляемых требований по составу решаемых задач и качества их решения, так и инструментально-методического обеспечения для проведения модельных экспериментов и проверки принимаемых структурных и функциональных решений.
Управление хаосом часто ассоциируется с задачей подавления хаотических колебаний, то есть перевода системы либо к устойчивым периодическим движениям, либо в состояние равновесия. В широком смысле, под управлением хаоса понимают преобразование хаотического поведения системы в регулярное или хаотическое, но с другими свойствами.
Возникающие при управлении хаосом задачи значительно отличаются от традиционных задач автоматического управления. Вместо классических целей управления — приведение траектории системы в заданную точку и приближение траектории к заданному движению, при управлении хаосом ставятся ослабленные цели: создание режимов с частично заданными свойствами, качественное изменение фазовых портретов систем, синхронизация хаотических колебаний и другие.
В отличие от традиционных "управленческих" работ в физических применениях теории хаоса упор делается не на поиск наиболее эффективного способа достижения цели, а на исследование принципиальной возможности ее достижения, на определение класса возможных движений управляемой физической системой.
Исследование динамики ансамблей, состоящих из большого числа нелинейных элементов, представляет собой одно из основных направлений развития нелинейных колебаний и волн. Главным фактором в динамике ансамблей автоколебательных систем, который приводит к упорядоченному пространственно–временному поведению, служит синхронизация элементов ансамбля. Многочисленные работы показывают что, пространственно-распределенные хаотические колебательные системы обладают богатыми свойствами. В некоторых из них наблюдается самосинхронизация при определенных параметрах системы. Под самосинхронизацией понимается, процесс, при котором идентичные элементы системы, каждый из которых характеризуется хаотической динамикой, будучи проинициализированы различным образом, с течением времени начинают колебаться синхронно без какого-либо внешнего воздействия.
При наличии внешнего воздействия на нелинейную динамическую систему мы получаем реакцию, которая отражает как внешние условия решения задачи, так и входные сигналы, которые характеризуют решаемую задачу. При таком подходе вместо создания модели для решения задачи, задается целевая установка — требуемый итог решения задачи и считается, что решение не единственное, во всяком случае, по форме представления образует многообразие, которое может быть проинтерпретировано и как единственное решение, и как некоторый набор базисных решений.
Укрупненные этапы использования таких сложных режимов функционирования хаотических систем для решения практических задач можно представить в виде следующей последовательности: задается начальное состояние системы и задается цель - достичь определенного состояния, затем запускается система и на нее подаются входные сигналы, соответствующие задаче. После прохождения некоторого переходного процесса система перейдет в некоторый аттрактор. Далее, используя малые возмущения системы, она переводится на траекторию, которая максимально близко пройдет рядом с требуемой точкой или последовательностью точек, соответствующих требуемому состоянию системы. Если такой аттрактор не находится, то подается случайный вход, чтобы перескочить на другой аттрактор, и так до достижения цели.
Формальное описание новой парадигмы в виде новой абстракции вычислительного устройства, обобщающего схему классической машины Тьюринга, показывает, как строго математически могут быть представлены предлагаемые концепции.
Основной проблемой при реализации нового подхода является подбор или создание адекватной аппаратной базы. Для решения задач моделирования нового высокопроизводительного вычислителя на нелинейных элементах можно использовать высокопроизводительные программируемые логические схемы. Однако, для получения системы, в которой смогут быть реализованы все свойства коллективного поведения элементов и решены задачи самосборки на кластеры, т.е. выполнена реконфигурация для адаптации под изменения в окружающей среде, необходимо искать адекватную аппаратную базу. В качестве одного из возможных вариантов реализации могут быть предложены реакционно-диффузионные среды, и тогда можно будет говорить о создании "жидкого" или химического высокопроизводительного вычислителя.
Как показывают многочисленные исследования в области нелинейной динамики, чем труднее задача, тем сложнее динамика системы. Новейшие исследования ведутся на молекулярном уровне с разными целями: создание новых материалов, новых лекарств, систем распознавания образов, новых устройств обработки информации и т.д. Такие исследования носят междисциплинарный характер и выполняются на стыке таких наук как молекулярная физика, биология, химия, математика, синергетика, экономика.
В результате применения предлагаемого подхода открываются новые возможности, снимающие прежние ограничения и позволяющие перейти к созданию новых универсальных вычислительных устройств, обладающих не только высокой производительностью, но и способностями подстраиваться под решаемую задачу.
Новые подходы требуют более четкого и современного понимания таких уже привычных понятий как информация, сигналы, данные, знания и управление.
11.5. Информация, сигналы, данные, знания и управление. Обработка информации в условиях неопределенности
Информация — это одна из фундаментальных категорий жизни современного общества, охватывающая практически все сферы производственной, научной, культурной и социальной деятельности, которые базируются на информационных процессах.
Ценность информации определяется степенью её достоверности и проезности для владельца и пользователей. Практически ценность определяется её способностью "подтолкнуть" субъекта к определенным действиям, т.е. его способности на основании полученной информации принять решение и сформировать некоторое управляющее воздействие (табл. 11.1). В этом смысле термины в заголовке этого раздела неразрывно друг с другом связаны и не могут друг без друга существовать (как двуликий Янус или Инь и Янь в китайской философии). Информация, "не подталкивающая" к действию, — бессмысленна, так же как и бессмысленны какие-то действия без лежащей в их основе информации.
| Информация | Управление |
|---|---|
| Человек заболел | Принять лекарство |
| Дерево, около которого мы стоим, начинает падать | Отойти вбок от оси падения дерева |
| Во всем доме погас электрический свет | Принять меры к исправлению повреждения в электроснабжении |
| Наметилась тенденция на существенное снижение курса акций из нашего инвестиционного портфеля | Начать продавать падающие акции |
| Зарегистрировано приближение подводной лодки противника к стратегически важному району | Отправить отряд кораблей для предотвращения проникновения подводной лодки противника или для контроля ее действий |
| В запретной зоне для полетов появился самолет противника | Постараться сбить вражеский самолет |
| В определенном регионе у населения существенно возрос интерес к выступлению некоторой эстрадной группы | Организовать концерт эстрадного коллектива в этом регионе |
Однако в большинстве случаев текущая информация быстро устаревает и ценность её уменьшается. Зависимость ценности информации от времени можно приближенно рассчитать по формуле:
 ,
,
где 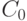 — ценность информации в момент её возникновения,
— ценность информации в момент её возникновения,  — время от момента возникновения до момента определения стоимости,
— время от момента возникновения до момента определения стоимости,  — время от момента возникновения информации до её устаревания.
— время от момента возникновения информации до её устаревания.
Величина  может меняться в широком диапазоне: для процессов ядерного взаимодействия оно измеряется в наносекундах, информация же о законах природы остается актуальной в течение многих веков.
может меняться в широком диапазоне: для процессов ядерного взаимодействия оно измеряется в наносекундах, информация же о законах природы остается актуальной в течение многих веков.
Количественные характеристики информации (метрические свойства) можно определить следующими основными методами: комбинаторными, статистическими, алгоритмическими и метрологическими. Все эти методы опираются в основе на принцип разнообразия состояний информационной системы.
Комбинаторная логарифмическая мера количества информации по Р. Хартли проста для вычисления и удобна при расчетах в силу аддитивности логарифмической функции:
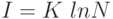 ,
,
здесь  — коэффициент пропорциональности, обусловленный избранной мерой количества информации (например, при
— коэффициент пропорциональности, обусловленный избранной мерой количества информации (например, при 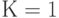 информация измеряется внатуральных числах; при
информация измеряется внатуральных числах; при 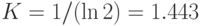 — в битах; при
— в битах; при 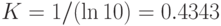 — в десятичных единицах),
— в десятичных единицах),  — число возможных дискретных состояний или число возможных сообщений о состоянии объекта или системы.
— число возможных дискретных состояний или число возможных сообщений о состоянии объекта или системы.
Из формулы видно, что эта мера инвариантна относительно любых свойств информации, безразмерна и в силу этого нечувствительна к содержанию информации в смысле её полезности. Из этого следует, что она практически бесполезна в задачах, где помимо количественных характеристик существенно смысловое содержание полученной информации.
В статистическом методе используется энтропийный подход — количество информации оценивается мерой уменьшения у получателя неопределнности (энтропии) выбора или ожидания событий после получения информации. Количество информации должно быть тем больше, чем ниже вероятность события. Такой подход широко используется при оценке количества информации, передаваемой по каналам связи. Выбор при приеме информации осущевляется между символами алфавита в принятом сообщении. Пусть, например, принятое по каналу связи сообщение состоит из N символов (без учета связи между символами в сообщении). Тогда для определения количества информации  в сообщении можно воспользоваться формулой К.Шеннона [146]:
в сообщении можно воспользоваться формулой К.Шеннона [146]:
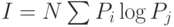 ,
, 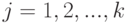 ,
,
где 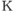 — количество символов в алфавите языка,
— количество символов в алфавите языка,  — вероятность появления в сообщении символа с номером
— вероятность появления в сообщении символа с номером  .
.
Здесь количество информации в двоичном представлении (в битах или байтах) зависит от двух величин: количества символов в сообщении и частоты появления того или иного символа для используемого алфавита. Этот подход также не отражает, насколько полезна полученная информация — он позволяет лишь определить затраты на передачу сообщения.
Алгоритмическая мера информационной сложности по А.Н. Колмогорову основывется на модели вычислительного процесса и понятии вычислимой функции. Кратко определить эти понятия можно следующим образом. Пусть  — множество возможных исходных данных, из которых складывается информационное сообщение,
— множество возможных исходных данных, из которых складывается информационное сообщение, 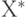 — множество конечных результатов применения определенного алгоритма, причем множество Х', включающее множество
— множество конечных результатов применения определенного алгоритма, причем множество Х', включающее множество  , — область применения алгоритма. Пусть также функция
, — область применения алгоритма. Пусть также функция  задает отображение
задает отображение
 , такое, что
, такое, что 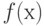 совпадает с результатом применения алгоритма к объекту
совпадает с результатом применения алгоритма к объекту  . Тогда
. Тогда  назывется вычислимой функцией, которая задается алгоритмом. Пусть далее рассматривается некоторое исходное множество объектов и устанавливается взаимно-однозначное соответствие между этим множеством и множеством двоичных слов конечной длины, т.е. слов вида
назывется вычислимой функцией, которая задается алгоритмом. Пусть далее рассматривается некоторое исходное множество объектов и устанавливается взаимно-однозначное соответствие между этим множеством и множеством двоичных слов конечной длины, т.е. слов вида 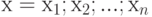 , где
, где 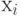 есть 1 или 0,
есть 1 или 0, 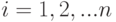 . Модуль
. Модуль  обозначает длину слова
обозначает длину слова  .
.
Конечное двоичное слово можно описать так, что его можно восстановить по его описанию. Например, двоичное слово 110001 10001 1000 словесно описать как "две единицы и три двойки, повторенные три раза подряд". Разные слова имеют разные описания, но и одно слово также может иметь несколько описаний. Возникает вопрос: как сравнивать между собой описания двоичного слова, чтобы выбрать из них самое простое?
Будем считать, что описание двоичного слова задается не словесно, а также в виде двоичного слова — аргумента некоторой вычислимой функции  . Для некоторого двоичного слова х существет множество
. Для некоторого двоичного слова х существет множество  всех двоичных слов, таких, что
всех двоичных слов, таких, что 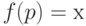 . Пусть далее
. Пусть далее
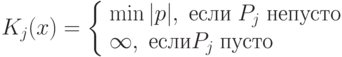
В этом случае 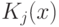 можно назвать сложностью слова
можно назвать сложностью слова  по
по  . Таким образом, сложность слова
. Таким образом, сложность слова  по
по  — это длина сaмого короткого двоичного слова, в котором содержится полное описание слова
— это длина сaмого короткого двоичного слова, в котором содержится полное описание слова  при фиксированном способе восстановления слов по их описаниям, т.е. при фиксированной функции
при фиксированном способе восстановления слов по их описаниям, т.е. при фиксированной функции  .
.
Тезаурусный подход — это рассмотрение информации с точки зрения количества полезных знаний, содержащихся в этом объеме. Согласно Ю.А.Шрейдеру, количество информации, извлекаемое человеком из сообщения, оценивается степенью изменения его знаний об объекте. Структурированные знания, представленные в виде понятий и отношений между ними, называются тезаурусом. Для передачи знаний необходимо, чтобы тезаурусы отправителя информации и получателя пересекались, иначе владельцы тезаурусов не поймут друг друга. Примером может служить принятое сообщение на чужом языке. В обществе сформировались две тенденции: развитие тезаурусов отдельных элементов (людей, сообществ, организованных структур) и выравнивание тезаурусов элементов общества.
Метрологический метод основан на количественном измерении объема информации, измеряемом количеством бит, количеством страниц текста, количеством файлов или длиной магнитной ленты или объемом диска с аудио или видеозаписью. Следует понимать, что этот метод использует относительные меры, так как одна и та же страница, лента, диск могут содержать разное количество информации — всё зависит от способа её кодирования и сжатия.
Рассмотренные формализованные подходы к формированию количественных мер не дают достаточной возможности для измерения и количественного описания ценности информации (прагматических характеристик) и содержательности (семантических характеристик). Прагматические характеристики можно подразделить на три группы.
В первую группу входят характеристики полезности информации на получателя, степень её влияния на состояние получателя и т. д. Ко второй группе относятся характеристики по качеству её связи с источником. Это характеристики важности информации для функционирования источника и показатели интенсивности генерации информации.
И, наконец, третья группа характеризуется внутренним качеством информации. Это такие качественные характеристики, как истинность, избыточность, полнота, актуальность, соответствие ожиданиям, степень обобщенности.
Напомним ещё раз, что полезность информации определяется тем, в какой степени она обеспечивает пользователю достижение поставленных целей. Данная характеристика тесно связана с характеристикой истинности информации, так как только максимальное сочетание истинности и полезности может уменьшить неопределенность ситуации и увеличить тем самым вероятность принятия правильного управленческого решения.
Обычно мы рассматриваем информацию как сообщение о том, что что-то произошло, т.е. одна из важнейших ее черт — изменение чего-то (объекта информации). Но информация возникает у кого-то или в чем-то (субъект информации).
Норберт Винер более шестидесяти лет тому назад провозгласил начало эры новой науки — кибернетики, одним из первых четко подметив, что "информационно-управленческая связь — это существенная часть любых явлений в живой и не живой природе" [35].
Введем для информации обозначение  , а для управления — u. Процесс принятия управленческого решения формализовано может быть записан как
, а для управления — u. Процесс принятия управленческого решения формализовано может быть записан как 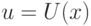 ,
, 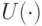 — некоторая функция от
— некоторая функция от  . Часто информацию x отождествляют с вектором состояний исследуемой системы. В этом случае говорят, что указанное выше соотношение задает обратную связь по состоянию.
. Часто информацию x отождествляют с вектором состояний исследуемой системы. В этом случае говорят, что указанное выше соотношение задает обратную связь по состоянию.
Реализация управления естественно влияет на информацию, способствуя новым изменениям объекта информации. Сформированное управление u поступает в систему и воздействует на состояние  , во многих случаях изменяя его. Связь между информацией и управлением можно представить в виде схемы рис. 11.5.
, во многих случаях изменяя его. Связь между информацией и управлением можно представить в виде схемы рис. 11.5.
Понимание неразрывной связи информации и управления снимает актуальность споров о первичности бытия или сознания, о поиске ответа на вопрос: что раньше — слово или дело?
Формализация процесса принятия решений приводит к необходимости определения понятий: сигналы, данные и знания.
Информация проявляет себя через изменения в тех или иных физических или социальных явлениях. Например, у заболевшего человека повышается температура тела. При падении дерева органы слуха фиксируют изменения в окружающих нас звуках, а глаза — изменения в отображаемой картинке.
При движении подводной лодки от ее гребных винтов распространяются специфические акустические волны. При приближении самолета и попадании его в зону видимости нашего радара от него отражается посылаемая радаром электромагнитная волна. Социальные изменения проявляются через выборочные опросы, голосования и т.п.
Физические и социальные явления и процессы, изменение которых можно зарегистрировать с помощью органов чувств или приборов, называются сигналами. Результаты регистрации называются данными.
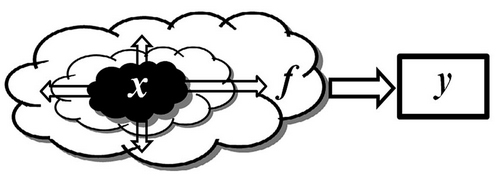
Обозначим через  — сигналы и через y — данные. Схема процесса регистрации сигнала показана на рис. 11.6.
— сигналы и через y — данные. Схема процесса регистрации сигнала показана на рис. 11.6.
Если нам доступны только данные наблюдений, то процесс принятия решения — это выработка управляющего воздействия на основе зарегистрированных данных по закону u=U(y).
Законы управления такого типа называются обратными связями по наблюдениям.
До сих пор мы оставляли открытым вопрос о том, как выбирать функцию обратной связи. В классической теории управления вводятся понятия наблюдаемости и управляемости, соответствующие возможности восстановить состояние объекта по наблюдениям или перевести объект в произвольное заданное состояние. Здесь мы не будем детально останавливаться на этих вопросах. В последующих разделах книги будет делаться упор на программную и аппаратную реализацию тех или иных управляющих воздействий, способы выбора которых будут отдельно описываться для каждого из случаев.
Осознание связей между зарегистрированными данными и информацией, а также способы выбора управляющих воздействий в зависимости от той или иной информации будем называть знаниями.
Например, регистрация температуры тела человека дала значение более 38,5 градусов Цельсия. Это говорит о том, что пациент болен. Информация о разливе Нила в определенный день по лунному календарю дала возможность создать первую крупную цивилизацию в Египте, позволив прогнозировать этот процесс и организовать посевы риса в строго определенное время.
В работоспособных системах имеющиеся знания позволяют на основании получаемых данных y формировать управляющие воздействия u, которые или дают какой-то выигрыш или позволяют как-то скомпенсировать негативную информацию. Без базы знаний постановка задачи о выработке обоснованных управляющих воздействий оказывается почти бессмысленной. Уточнение "почти" включено, т.к. при априорном отсутствии знаний их зачастую можно приобрести с течением времени.
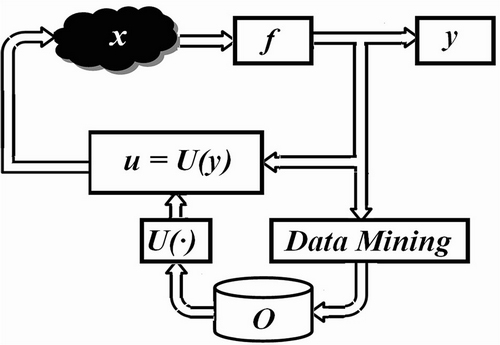
Совокупность накопленных определений, понятий и знаний относительно некоторой области называют онтологией. Знания в онтологию поступают как "извне" в виде постулируемых законов ("откровений"), так и формируются "внутри" системы при обработке данных. Процесс извлечения знаний из данных определяет круг задач такой новой бурно развивающейся области как Data Mining.
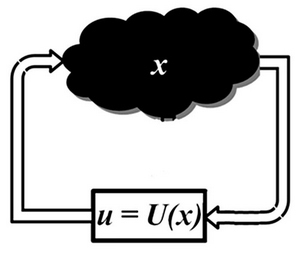
В контексте задач управления онтология служит своеобразной базой данных (знаний), из которой выбирается наиболее адекватная текущей ситуации функция управления 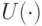 (рис. 11.7).
(рис. 11.7).
Изменение набора знаний со временем очень важная черта, позволяющая адаптироваться к изменяющимся условиям.
Реакция на информацию (управляющее воздействие) может быть ранее определена "извне" в соответствии с некоторыми правилами (законами), записанными в онтологии, либо формироваться "изнутри", адаптируясь к изменениям (т.е. пытаясь найти лучшее решение для поведения в изменившейся ситуации).
Процессы управления и накопления знаний часто являются взаимно противоречивыми. Целью управления обычно является достижение какого-то устойчивого состояния (по возможности не изменяющегося со временем). В этом состоянии "очень мало информации", и, следовательно, невозможно выявить или установить новые связи, значения и т.п. Например, о лежащем в пыли на обочине дороги камне мало что можно узнать при поверхностном осмотре. Его неизменность дает мало информации (характеристик изменений). Нужно совершить какое-либо действие — камень надо перевернуть, поднять, толкнуть или расколоть для получения какой-то информации. Это приводит к тому, что при синтезе законов управления часто сталкиваются с проблемой недостаточной вариативности последовательности наблюдений.
А.А. Фельдбаум сформулировал известный принцип "дуального управления": управляющие воздействия должны быть в известной мере изучающими, но, в известной мере, направляющими. Например, если цель адаптивного управления состоит в минимизации отклонения вектора состояния системы от заданной траектории, то это часто приводит к вырожденной последовательности наблюдений, в то время как для успешного проведения идентификации неизвестных параметров системы должно быть обеспечено "разнообразие" наблюдений.
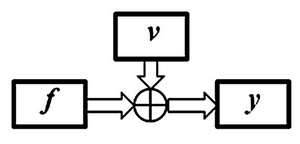
На практике реальная ситуация осложняется еще и тем, что при получении данных в любом регистрационном устройстве к сигналам добавляются некоторые помехи или ошибки  (рис. 11.8).
(рис. 11.8).
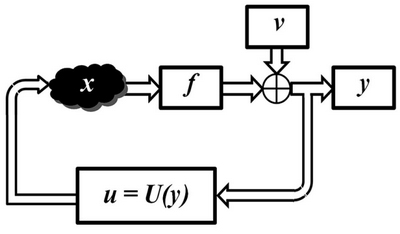
Структурная схема системы с обратной связью при наблюдениях с помехами приведена на рис. 11.9.
Хорошо поставленный эксперимент при тщательном измерении позволяет в некоторых случаях свести ошибки  к минимуму:
к минимуму:
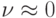 . Если первоначально "чистый" эксперимент не поставить, то стараются сделать его таковым с течением времени, т.е.
. Если первоначально "чистый" эксперимент не поставить, то стараются сделать его таковым с течением времени, т.е. 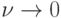 .
.
В других случаях в задачах о наблюдении физических явлений часто достаточно обоснованно предполагают статистическую природу помех, но возможны осмысленные постановки задачи и при произвольных внешних помехах .
Сложившаяся к настоящему времени парадигма использования вычислительных устройств базируется на исторически сложившемся разделении процессов обработки данных и принятия управленческих решений (после обработки). Основания этого разделения прослеживаются в истории развития средств вычислительной техники. Первоначально компьютеров было мало и они, занимая огромные пространства, требовали специальных условий для эксплуатации. Формировались особые вычислительные центры для объединенного решения в одном месте множества разных задач, причем до сих пор актуальным остается одно из приоритетных направлений развития — создание суперкомпьютеров. Встроенным устройствам традиционно отводилась роль или устройств для сбора данных, или устройств для реализации определенных управляющих воздействий. В некоторых случаях они использовались как регуляторы в простых контурах обратной связи. Суперкомпьютеры брали на себя выполнение задач Data Mining.
Но надо четко отдавать себе отчет в применимости этой традиционной парадигмы. В природе и обществе информационно-управленческие связи являются основой связи многих явлений и процессов. Искусственно разделяя процессы обработки данных и управления, мы существенно снижаем наши возможности использования информационно-коммуникационных технологий.
Надо ли разделять процессы обработки данных и управления?
С начала XXI века в теории управления заметен всплеск интереса к тематике поиска данных, управления в сетях, коллективному взаимодействию, мультиагентным технологиям и т.п. Это во многом связано с технологическим прогрессом. Сейчас миниатюризация и быстродействие средств вычислительной техники достигли такого уровня, что стало возможным в миниатюрных встроенных системах реального времени использовать вычислительные блоки, соизмеримые по производительности с мощными компьютерами XX веке. Все чаще "простые" встроенные электронные устройства заменяются сложнейшими "интеллектуальными встроенными системами".
Новые альтернативы и новые технологии позволяют по-новому взглянуть на ставшую уже традиционной область поиска и извлечения данных (Data Mining). В литературе все чаще появляются мысли о возрождении науки "Кибернетика" с большой буквы, о появлении "неокибернетики" .
Теория управления начала свой путь с регуляторов механических систем в XIX века. К концу ХХ века она прошла этап глубокой интеграции с цифровыми технологиями обработки данных и принятия решений, а в XXI веке стала фокусироваться на сетях объектов. В настоящее время теория управления выступает "собирателем" трех основных компонент прогресса второй половины ХХ века:
- теории управления (Control Theory),
- теории коммуникаций (Communication Theory)
- информатики (Computer Science)
Таким образом, применение кибернетической парадигмы, при которой процессы "добычи знаний" и получения информации будут учитывать неразрывную связь информации и управления и опираться на нее, обязательно приведут к формированию нового качества в обработке данных и извлечении знаний. Тогда можно поставить следующий вопрос: может ли дать какое-то новое качество в обработке данных и извлечении знаний применение кибернетической парадигмы, при которой процессы получения информации и "добычи знаний" и будут учитывать неразрывную связь информации и управления (и опираться на нее)?
Для иллюстрации положительного ответа в книге
О. Н. Граничина и соавторов [56] рассмотрены несколько примеров повышения эффективности процессов обработки данных и управления при изменении вычислительной парадигмы. Один из них основан на использовании замкнутых стратегий управления в условиях неопределенностей. Для объекта управления (ОУ) с входами  и выходами
и выходами 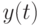 , и предположим, что задано начальное состояние
, и предположим, что задано начальное состояние  , и динамика объекта при
, и динамика объекта при
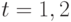 описывается уравнением
описывается уравнением
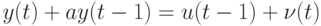
с неопределенностями 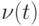 и
и  двух типов:
двух типов:
- динамические возмущения
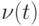 неизвестны и ограничены для всех
неизвестны и ограничены для всех  , но могут меняться со временем;
, но могут меняться со временем; - коэффициент модели a также неизвестен и ограничен:
![a\in [1;5]](/sites/default/files/tex_cache/e31897d17ce8d705dd69e6bbe653d0f0.png) , но он не может изменяться со временем.
, но он не может изменяться со временем.
Можно выбрать входы  и
и 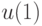 . Цель – минимизировать
. Цель – минимизировать  .
.
При сравнении качества минимаксной оптимизации
![J=sup_{a\in[1;5]}sup_{|\nu(1)\le1,|\nu(2)\le1||}|y(2)|\to\min_{u(0),u(1)}](/sites/default/files/tex_cache/cb15c843238cfcacfdc79fd9fb2b7736.png)
для двух классов допустимых стратегий управления: программных (всевозможные пары  ,
, 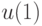 ) и замкнутых (в которых в момент времени
) и замкнутых (в которых в момент времени 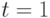 можно использовать наблюдение
можно использовать наблюдение 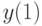 и управление
и управление  ), получились два существенно отличающихся ответа
), получились два существенно отличающихся ответа 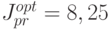 и
и 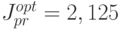 .
.
Зависимость качества управления от задания класса неупреждающих стратегий адекватно понимается далеко не всех публикациях. Если все параметры объекта управления известны и помехи отсутствуют, то множества программных и замкнутых стратегий управления оказываются совпадающими.
Другой пример из той же книги О.Н. Граничина и соавторов показывает возможность получения обоснованных оценок неизвестных параметров системы в условиях произвольных внешних возмущений в измерениях при допущении возможности активно влиять на результаты измерений, выбирая рандомизированные управления (входы).
В случае больших и сложных систем, состоящих из похожих компонентов, в статистической механике и физике оправдал себя подход Крылова-Боголюбова, основанный на усреднении данных, активно развиваемый, начиная с работ Гиббса, основываясь на теории Лебега. Для большого количества физических и социальных явлений при отсутствии внешних воздействий выполняется гипотеза эргодичности, когда среднее пространственное значение той или иной характеристики различных компонент системы, подсчитанное в определенный момент времени, совпадает со средним временным значением одной из компонент. При этом идеи усреднения хорошо согласуются и с конструкцией многих регистрирующих приборов, принцип действия которых часто заключается в том, что они выдают в результате некоторое среднее значение той или иной характеристики за определенный интервал времени.
Если регистрирующий прибор усредняет поступающие при 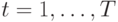 "мгновенные" сигналы
"мгновенные" сигналы  с помехами
с помехами  , то на выходе прибора получаем
, то на выходе прибора получаем

При случайной природе помех v(t) и известном среднем значении m в предположении об их независимости, одинаковой распределенности, конечности дисперсии, в силу закона больших чисел теории вероятностей, увеличивая T, можно добиться сколь угодно малой вероятности отличия второго слагаемого в последней формуле от среднего значения помехи. Т.е. по данным y и m можно достаточно точно определить среднее значение сигнала  , определяемое первым слагаемым в последней формуле.
, определяемое первым слагаемым в последней формуле.
Что делать, если помехи 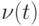 не являются случайными (статистическими)? Например,
не являются случайными (статистическими)? Например, 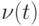 — значения неизвестной функции (т.е. произвольные значения).
— значения неизвестной функции (т.е. произвольные значения).
В рамках классической парадигмы обработки данных постановка задачи об оценивании среднего значения сигнала регистрируемого на фоне произвольных помех кажется абсурдной, но не из-за ее практической бессмысленности (это очень важная задача), а из-за невозможности ее как-то решить.
Для простоты рассмотрим случай скалярных наблюдений. Модернизируем постановку задачи, включив в модель наблюдений управляющее воздействие (вход)  .
.
Следуя парадигме неразрывности информации и управлений, будем считать, что регистрируемый сигнал  в момент времени t напрямую определяется текущим входом
в момент времени t напрямую определяется текущим входом  и некоторым неизвестным параметром
и некоторым неизвестным параметром  (неизвестным коэффициентом усиления/ослабления входа)
(неизвестным коэффициентом усиления/ослабления входа)
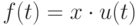
Модель наблюдений можно переписать в виде:
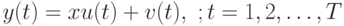
При этом мы можем: а). выбирать входы  , б). измерять выходы
, б). измерять выходы 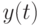 .
.
При использовании  получаем традиционную задачу об оценивании неизвестного параметра
получаем традиционную задачу об оценивании неизвестного параметра  , наблюдаемого на фоне помех.
, наблюдаемого на фоне помех.
На самом деле с такими постановками задач мы сталкивались уже в школьной программе изучая физические эксперименты, в которых измеряется результат того или иного воздействия на систему. Например, прикладывая к пружине разные усилия, мы получаем разные длины растяжения или сжатия. Но полученные результаты — это не произвольные числа, они определяются характеристиками (параметрами) самой пружины (коэффициентом упругости). Кроме того, на результат влияют и конкретные условия проведения эксперимента, определяемые внешними силами, помехами и т.п. (в частности, трение).
Другой типичный пример из области исследования материалов, или недр, или разнообразных применений дистанционного зондирования показан на рисунке 11.10.
Источник посылает в пространство некоторый сигнал  (излучение), или поток частиц (электроны, или
(излучение), или поток частиц (электроны, или  -частицы и т.п.), или волну той или иной природы (акустическую или электромагнитную), причем интенсивность потока можно варьировать и точно измерять (например, мерить величину "ушедшего" заряда). При встрече с мишенью либо сигнал отражается (эхо-акустика, радар и т.п.), либо его взаимодействие с мишенью порождает некоторый новый "отраженный" сигнал
-частицы и т.п.), или волну той или иной природы (акустическую или электромагнитную), причем интенсивность потока можно варьировать и точно измерять (например, мерить величину "ушедшего" заряда). При встрече с мишенью либо сигнал отражается (эхо-акустика, радар и т.п.), либо его взаимодействие с мишенью порождает некоторый новый "отраженный" сигнал 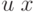 (может быть и другой природы), интенсивность которого потом измеряется детектором. Требуется определить неизвестный параметр
(может быть и другой природы), интенсивность которого потом измеряется детектором. Требуется определить неизвестный параметр  , который либо равен нулю, что соответствует отсутствию мишени с заданными отражающими свойствами, либо при положительной величине
, который либо равен нулю, что соответствует отсутствию мишени с заданными отражающими свойствами, либо при положительной величине  характеризует те или иные физические характеристики: дальность до мишени, ее размер, отражающие свойства материала и т. п.
характеризует те или иные физические характеристики: дальность до мишени, ее размер, отражающие свойства материала и т. п.
Общим в рассмотренных примерах является возможность активного влияния экспериментатора на результат наблюдений (возможность подать "входное воздействие").
В каком максимально широком классе помех 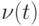 все-таки реалистично попытаться получить осмысленный ответ в задаче об оценивании неизвестного параметра
все-таки реалистично попытаться получить осмысленный ответ в задаче об оценивании неизвестного параметра  ?
?
Естественно при записи уравнения, задающего модель наблюдений, предположить, что второе слагаемое в правой части 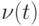 включает в себя все неопределенности, влияющие на выход
включает в себя все неопределенности, влияющие на выход 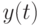 , которые никак не связаны с
, которые никак не связаны с  , т.к.
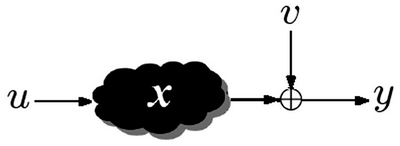
, т.к.  явно входит только в первое слагаемое в правой части. Такие помехи будем называть "внешними", подчеркивая их независимость от внутренних входов, подаваемых в систему. Можно ли как-то решить задачу в таком классе неопределенностей? Поясним схему задачи, используя рисунок 11.11.
явно входит только в первое слагаемое в правой части. Такие помехи будем называть "внешними", подчеркивая их независимость от внутренних входов, подаваемых в систему. Можно ли как-то решить задачу в таком классе неопределенностей? Поясним схему задачи, используя рисунок 11.11.
Система является "черным ящиком" с входом  и выходом
и выходом 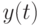 . Система характеризуется неизвестным нам параметром
. Система характеризуется неизвестным нам параметром  (например, в примере с пружиной
(например, в примере с пружиной  — это коэффициент упругости). Экспериментатор может выбирать воздействия на систему
— это коэффициент упругости). Экспериментатор может выбирать воздействия на систему  , которые поступают на вход "черного ящика" (в примере с пружиной мы можем растянуть или сжать ее на расстояние
, которые поступают на вход "черного ящика" (в примере с пружиной мы можем растянуть или сжать ее на расстояние  ). На выходе "черного ящика" к результату добавляется внешняя помеха
). На выходе "черного ящика" к результату добавляется внешняя помеха 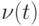 , которая никак не связана с "внутренними" процессами внутри "черного ящика" (в примере с пружиной выход с помехой — погрешности измерений, вносимые динамометром).
, которая никак не связана с "внутренними" процессами внутри "черного ящика" (в примере с пружиной выход с помехой — погрешности измерений, вносимые динамометром).
Уточним задачу. Требуется по последовательности входов и выходов 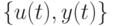 определить неизвестный параметр
определить неизвестный параметр  при отсутствии каких-либо ограничений на последовательность внешних помех
при отсутствии каких-либо ограничений на последовательность внешних помех 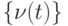 .
.
Не кажется ли такая постановка задачи абсурдной?
С детерминистской точки зрения — конечно! Не может быть никакого детерминированного алгоритма, дающего хотя бы в каком-то смысле здравый ответ (кроме бессмысленного решения — вся числовая ось!). Предложив в качестве ответа любое из чисел или даже какой-то интервал при конечном (или счетном) числе наблюдений, всегда можно будет подобрать такие 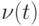 , что при следующем наблюдении предложенный ответ будет неверным.
, что при следующем наблюдении предложенный ответ будет неверным.
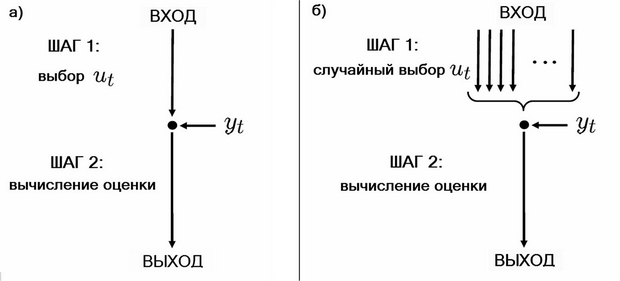
Общий алгоритм последовательного оценивания неизвестного параметра x состоит из двух шагов:
- Выбор входа
 .
. - Оценивание параметра
 на основе полученных данных
на основе полученных данных 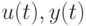 (например, вычисление числовой оценки
(например, вычисление числовой оценки  или множества
или множества  , содержащего
, содержащего  ).
).
Если бы в условиях задачи дополнительно можно было бы предположить случайную (вероятностную) природу помех 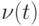 , то при выполнении условий закона больших чисел можно было бы говорить об оценивании неизвестного параметра
, то при выполнении условий закона больших чисел можно было бы говорить об оценивании неизвестного параметра  путем простого усреднения данных наблюдения.
путем простого усреднения данных наблюдения.
Если наблюдения проводить также со случайной помехой, но у которой среднее значение  было бы неизвестно, то результаты усреднения отличались бы от истинного значения
было бы неизвестно, то результаты усреднения отличались бы от истинного значения  , на неизвестную величину
, на неизвестную величину  .
.
Несмотря на кажущуюся абсурдность постановки задачи оценивания при произвольных внешних помехах, из практических потребностей часто ее все-таки приходится решать.
Альтернативой оказываются рандомизированные алгоритмы, в которых выполнение одного или нескольких шагов производимых пользователем основано на случайном правиле (т.е. среди многих детерминированных правил одно выбирается случайно в соответствии с вероятностью 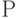 ).
).
В зависимости от специфики конкретной задачи вероятность Р или является искусственным элементом, вводимым в алгоритм для улучшения разрешимости проблемы, или в рассматриваемой системе могут присутствовать измеряемые случайные элементы. Выбор этой вероятности Р является частью конструирования алгоритма.
Рассмотрим следующее правило случайного выбора для первого шага рандомизированного алгоритма последовательного оценивания неизвестного параметра 
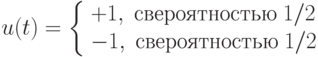
На втором шаге по известным парам значений 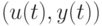 формируем величины
формируем величины 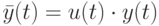 . Для "новой" последовательности наблюдений справедлива похожая на исходную модель
. Для "новой" последовательности наблюдений справедлива похожая на исходную модель
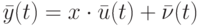
в которой 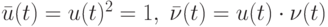 .
.
Если 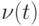 — внешние помехи, то естественно считать, что они независимы с нашим рандомизированным правилом выбора входов на шаге 1. Следовательно,
— внешние помехи, то естественно считать, что они независимы с нашим рандомизированным правилом выбора входов на шаге 1. Следовательно,
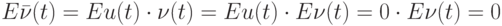
т.е. "в новой модели" наблюдений задача об оценивании неизвестного параметрa x, не имевшая решения, превращается при использовании случайного правила выбора входов на шаге 1 рандомизированного алгоритма в "стандартную" задачу об оценивании неизвестного параметра x, наблюдаемого на фоне независимых центрированных помех (рис. 11.12).
В упоминавшейся выше книге О.Н. Граничина и соавторов приведены алгоритмы, обоснования и примеры численного моделирования, дающие при фиксированном малом (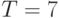 ) количестве наблюдений доверительные интервалы для
) количестве наблюдений доверительные интервалы для  с задаваемой априорно вероятностью
с задаваемой априорно вероятностью 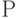 .
.
Итак, для, казалось бы, абсурдной задачи об оценивании параметра при произвольных внешних помехах, с которой принципиально не может справиться ни один детерминированный алгоритм, внесение рандомизации в процесс выбора входов позволяет получить вполне осмысленные результаты, позволяя говорить о вероятностной успешности рандомизированного алгоритма с некоторым параметром (вероятностью) 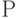 . Достижение успешных результатов с высокой степенью вероятности, в отличие от детерминированного случая, соответствует компромиссу: если полностью гарантированный результат получить невозможно, то лучше иметь какую-то гарантию, чем не иметь ничего!
. Достижение успешных результатов с высокой степенью вероятности, в отличие от детерминированного случая, соответствует компромиссу: если полностью гарантированный результат получить невозможно, то лучше иметь какую-то гарантию, чем не иметь ничего!
Конечно, не во всех задачах компромисс возможен. Во многих случаях нужен ответ, гарантированный на 100%. Но, "защищая" рандомизированные алгоритмы, надо отметить, что уровень достоверности 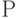 обычно является параметром алгоритма, который может быть настроен пользователем. Параметр
обычно является параметром алгоритма, который может быть настроен пользователем. Параметр 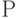 ослабляет понятие детерминированной разрешимости, для которой вероятность успеха может быть только 0 или 1 — образно выражаясь, результат "черный" или "белый". Переходя к рандомизированным алгоритмам,
ослабляет понятие детерминированной разрешимости, для которой вероятность успеха может быть только 0 или 1 — образно выражаясь, результат "черный" или "белый". Переходя к рандомизированным алгоритмам,  становится непрерывным параметром, пробегающим интервал
становится непрерывным параметром, пробегающим интервал
![[0; 1]](/sites/default/files/tex_cache/f083648758df2ddf9560f0b17ac28d3b.png) , задавая тот или иной "оттенок серого".
, задавая тот или иной "оттенок серого".
Отметим, что альтернативный вероятностный подход к решению задачи оценивания — байесовский, при котором присутствующим в системе помехам 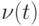 априори приписывается вероятностная природа
априори приписывается вероятностная природа  , но его невозможно применить при произвольных внешних помехах (в худшем случае), т. к. все выводы имеют вероятностную основу предположений о системе.
, но его невозможно применить при произвольных внешних помехах (в худшем случае), т. к. все выводы имеют вероятностную основу предположений о системе.
По смыслу байесовский и рандомизированний подход совершенно различны с практической точки зрения. В байесовском —  описывает вероятность того или иного значения помехи
описывает вероятность того или иного значения помехи 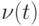 по сравнению с другими, т. е. выбор
по сравнению с другими, т. е. выбор  является частью модели задачи. В отличие от этого вероятность
является частью модели задачи. В отличие от этого вероятность  в рандомизированном подходе является тем, что мы искусственно выбрали и используем. Вероятность
в рандомизированном подходе является тем, что мы искусственно выбрали и используем. Вероятность  существует только в нашем алгоритме, и, следовательно, нет традиционной проблемы плохой модели, как это может случиться с
существует только в нашем алгоритме, и, следовательно, нет традиционной проблемы плохой модели, как это может случиться с  при байесовском подходе.
при байесовском подходе.
На практике очень часто оказывается, что классические методы решения задач либо неприменимы к реальной жизни (нетрудно представить себе, что значит попытаться решить задачу управления предприятием в непредсказуемой динамичной обстановке современного бизнеса), либо они требуют огромных объемов расчетов (для которых не хватит мощности всех современных компьютеров), либо они вовсе отсутствуют. Во многих таких случаях альтернативой оказываются мультиагентные технологии, суть которых заключается в принципиально новом методе решения задач. В отличие от классического способа, когда проводится поиск некоторого четко определенного (детерминированного) алгоритма, позволяющего найти наилучшее решение проблемы, в мультиагентных технологиях решение получается автоматически в результате взаимодействия множества самостоятельных целенаправленных программных модулей — так называемых агентов [38].
Как и в двух предыдущих примерах, одной из важнейших характеристик мультиагентных технологий является отказ от традиционной для информационных технологий парадигмы разделения процессов получения информации и принятия управленческих решений. В случае сложных систем, состоящих из огромного числа взаимодействующих динамических объектов, возможность получения реальной "мгновенной картины мира" можно вообразить себе только теоретически, на практике во время сбора всей необходимой информации "картина мира" может существенно измениться.
При использовании мультиагентных технологий компоненты системы начинают взаимодействовать и реализовывать те или иные управляющие воздействия самостоятельно, не дожидаясь "команды из центра". Оказывается, что во многих практических управленческих задачах такая парадигма позволяет эффективно управлять системами в то время, как задача о сборе всей информации может так и оставаться до конца не решенной.
Задачи управления и распределенного взаимодействия в сетях динамических систем привлекают в последнее десятилетие внимание все большего числа исследователей. Во многом это объясняется широким применением мультиагентных систем в разных областях. Это ? автоматическая подстройка параметров нейронных сетей распознавания, балансировка загрузки узлов вычислительных сетей, управление формациями, работа в распределенных сенсорных сетях, управление перегрузкой в сетях связи, взаимодействие групп беспилотных летательных аппаратов (БПЛА), относительное маневрирование групп космических аппаратов, управление движением мобильных роботов, синхронизация нагрузки в энергосистемах. Для многих распределенных систем, выполняющих определенные действия параллельно, чрезвычайно актуальна задача разделения пакета заданий между несколькими вычислительными потоками (устройствами).
Подобные задачи возникают не только в вычислительных сетях, но также и в производственных сетях, сетях обслуживания, транспортных, логистических сетях и др. Оказывается, что при естественных ограничениях на связи, децентрализованные стратегии способны эффективно решать такого типа задачи. Решение таких задач существенно усложняется при практическом применении из-за изменчивости структуры связей, обмене неполной информацией, которая, кроме того, обычно измеряется с помехами, а также из-за эффектов квантования (дискретизации), свойственных всем цифровым системам.
Для группы взаимодействующих агентов, обменивающихся с задержкой неполной информацией в дискретные моменты времени при изменяющейся топологии связей для решения задачи о достижении консенсуса предложен и обоснован алгоритм стохастической аппроксимации с убывающим размером шага, который позволяет каждому агенту получать информацию о состоянии своих соседей при одновременном снижении воздействия помех.
Суть алгоритма — в децентрализованной балансировке. Каждый агент принимает решение о перераспределении заданий "с соседями" только на основании текущей оперативной информации о своей и их загруженности. Типичное время, за которое вся система приходит к "оптимальной загрузке" соизмеримо со временем, которое было бы затрачено на получение всей информации о загруженности сети. При классическом централизованном подходе далее надо было бы решить очень сложную задачу об оптимальном расписании, а потом еще и перераспределить задания, НО за это время новые задания и изменения в окружающей среде (топологии связи) могут сделать всю эту работу напрасной. Подробнее о мультиагентных технологиях и системах будет рассказано далее.