Машина вывода Пролога

Данная глава посвящена устройству вычислений в Прологе. Дается представление о машине вывода Пролога. Рассматривается конструкция сложных термов и понятие отрицания в языке Пролог. Показывается, как использовать трассировку в PIE и отладчик системы Visual Prolog.

Основными механизмами машины вывода Пролога являются унификация и откат. При унификации термов и атомарных формул находится наибольший общий унификатор. Откат используется для поиска всех решений.

2.1. Унификация

Формулы и называются унифицируемыми, если существует такая подстановка термов вместо переменных, что 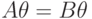. Подстановка ? называется при этом унификатором формул и .

Например, формулы 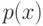и унифицирует любая из подстановок и .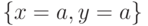

Композицией подстановок и 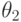называется подстановка , которая получается из подстановки применением к ее равенствам подстановки 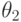, так что равенства 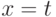преобразуются в равенства 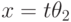, с последующим удалением равенств вида , и добавлением равенств 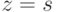из 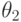для переменных , не встречающихся в левых частях равенств 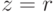в подстановке .

Например, композицией подстановок и 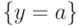является подстановка .

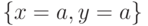Унификатор формул и называется наибольшим общим унификатором, если для любого другого унификатора этих формул найдется такая подстановка 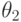2, что .

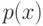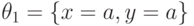Например, наибольшим общим унификатором формул и является подстановка . Если, в частности, , то, взяв 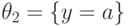, получим: .

Построение наибольшего общего унификатора двух формул сводится к последовательному выявлению и устранению их различий.

Множество рассогласований формул и — это самая левая пара несовпадающих термов, стоящих в этих формулах на одинаковых позициях.

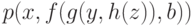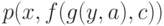Например, множество рассогласований формул и равно .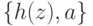

Алгоритм поиска наибольшего общего унификатора формул и заключается в следующем. На нулевой итерации полагается , и 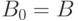. На итерации , начиная с 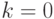, выполняются следующие действия:

1. если 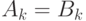, то алгоритм завершает свою работу, и наибольший общий унификатор полагается равным 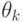, иначе находится множество рассогласований 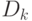формул 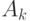и 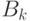и выполняется переход к шагу 2;
2. если 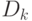содержит переменную и терм , в который не входит переменная , то строится подстановка 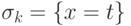и выполняется переход к шагу 3, иначе алгоритм завершает свою работу — формулы и не унифицируемы;
3. вычисляются формулы и и подстановка и выполняется переход к итерации .

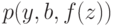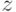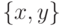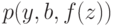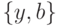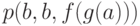Например, найдем наибольший общий унификатор формул и с переменными , и и константами и . Множество рассогласований имеет вид: . Применим к формулам подстановку и получим формулы и . Множество рассогласований этих формул равно . Соответственно, применим к этой паре формул подстановку и получим формулы и 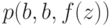. Множество рассогласований последних формул выглядит следующим образом: 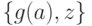. Применим к данным формулам подстановку 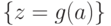и получим полностью совпадающие формулы, равные 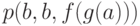. Наибольший общий унификатор равен композиции подстановок:

.

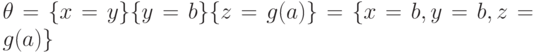2.2. Процедурная семантика логической программы

Процедурная семантика программы отвечает на вопрос, как устроены вычисления. Вычисления в классическом случае проводятся в соответствии с методом SLD-резолюции (Selected Linear Defined Resolution) [7, 9].

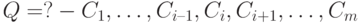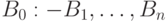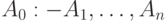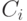Пусть — запрос к логической программе, — вариант правила , такой что в нем и в запросе нет совпадающих переменных, и — наибольший общий унификатор формул и .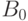

SLD-резольвентой запроса и правила с подстановкой называется запрос .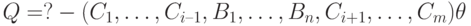

Положим . Частичным SLD-резолютивным вычислением называется последовательность троек , в которой 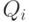является SLD-резольвентой запроса и правила с подстановкой . Такое вычисление называется успешным, если на некотором шаге получается пустой дизъюнкт: 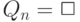. Ответом на запрос, в случае успешного вычисления, является композиция подстановок 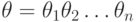, ограниченная переменными запроса .

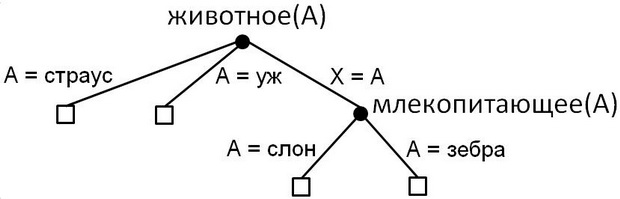
Процедурным значением программы является множество простых замкнутых целей из эрбранова базиса, которые выводятся из программы с помощью SLD-резолютивного вывода. Вернемся к программе (см. п. 1.1):

млекопитающее("слон").
млекопитающее("зебра").

животное("страус").
животное("уж").
животное(X):- млекопитающее(X).

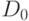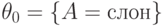Рассмотрим цель . SLD-резольвентой этого запроса и правила вида с подстановкой является запрос . SLD-резольвентной этого запроса и правила с пустым телом с пустой подстановкой является пустой запрос. Таким образом, цель выводится из программы. Легко проверить, что все цели из минимальной модели 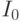выводятся из программы, а остальные цели из эрбранова базиса не выводятся. Это верно и в общем случае: декларативное и процедурное значения классической логической программы совпадают.

Пространство вычислений в классическом Прологе представляется в виде дерева, вершинами которого являются SLD-резольвенты родителя и одного из правил, а ребра соответствуют унифицирующим постановкам. Корень дерева — это цель программы. Листьями являются пустые запросы, которые завершают успешные вычисления, и запросы, не имеющие SLD-резольвент, которые завершают тупиковые вычисления (рис. 2.1). Это дерево называется деревом SLD-резолютивных вычислений.

Рис. 2.1. Дерево SLD-резолютивных вычислений для запроса животное(A)

Вычисления в языке Пролог соответствуют обходу дерева в глубину. Правила программы упорядочиваются сверху вниз. Выделяется самая левая подцель запроса, затем на каждом шаге вычисления к нему применяется первое еще неиспользованное правило программы для данного предикатного символа, при этом в стеке запоминается возможное разветвление — следующее правило. Когда вычисление заходит в тупик или успешно завершается, происходит возврат в точку последнего разветвления, при этом результаты всех предыдущих подстановок отменяются. Вычисления заканчиваются, когда стек разветвлений становится пустым. Недостатком такой стратегии является существование возможности попасть на бесконечную ветвь дерева вычислений, с которой программа не может выбраться, теряется полнота вычислений. Полнотой обладает обход дерева в ширину, он обнаруживает все успешные вычисления произвольного запроса. Но обход в ширину требует слишком большого расхода памяти, поэтому стандартной стратегией вычислений в Прологе является поиск в глубину.