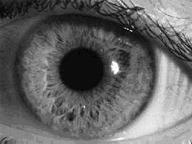
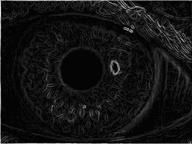
Использование шейдеров с помощью языка HLSL. Графический процессор
Рассмотрим теперь некоторые методы обработки изображения с использованием пространственных процессов. В этом случае элемент изображения получает новое значение на основе группы элементов, примыкающих к данному. Область (окрестность) примыкания представляет собой группу элементов изображения использующаяся в пространственных процессах. Как правило, область примыкания есть квадратная матрица нечетной размерности с центром в обрабатываемом элементе.
Пространственная частота изображения – скорость изменения яркости по координатам. Говорят, что присутствует высокая частота в изображении, если яркость меняется очень сильно. Одной из центральных задач в обработке изображений является построение пространственного фильтра. Фильтр позволяет усилить или ослабить компоненты различной частоты. Пространственный фильтр – процесс, который способен выделить (подчеркнуть) компоненты определенной частоты. Двумерный фильтр устроен следующим образом. Берется матрица размером 3х3, 5х5, 7х7 и т.д. и на ней определяется некоторая функция. Упомянутая матрица называется окном или апертурой, а заданная на нем функция – весовой или функцией окна. Каждому элементу окна соответствует число, называемое весовым множителем. Совокупность всех весовых множителей и составляет весовую функцию. Нечетные размеры апертуры объясняются однозначностью определения центрального элемента. Фильтрация осуществляется перемещением окна (апертуры) фильтра по изображению. В каждом положении апертуры выполняются однотипные действия, которые определяют так называемый отклик фильтра. Весовая функция в процессе перемещения остается неизменной. В каждом положении окна происходит операция свертки – линейная комбинация значений элементов изображения: 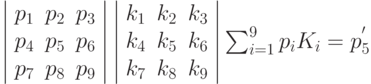 ,
где
,
где 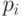 - элементы области примыкания,
- элементы области примыкания, 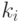 - весовые множители,
- весовые множители, 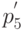 - новое значение пикселя. При каждом положении окна весовая функция поэлементно умножается на значение соответствующих пикселей исходного изображения и произведения суммируются. Полученная сумма называется откликом фильтра и присваивается тому пикселю нового изображения, который соответствует положению центра окна. Низкочастотный фильтр – процесс, который ослабляет высокочастотные компоненты и усиливает роль низкочастотных.
- новое значение пикселя. При каждом положении окна весовая функция поэлементно умножается на значение соответствующих пикселей исходного изображения и произведения суммируются. Полученная сумма называется откликом фильтра и присваивается тому пикселю нового изображения, который соответствует положению центра окна. Низкочастотный фильтр – процесс, который ослабляет высокочастотные компоненты и усиливает роль низкочастотных.
Сглаживание изображения реализуется с помощью следующих ядер.
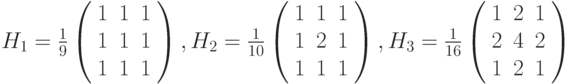
Следует заметить, что общая яркость исходного изображения и результирующего будет одинаковой.
Фильтры высокой частоты применяются для выделения таких деталей, как контуры, границы или для повышения резкости изображения. Каждый скачок яркости и каждый контур представляют собой интенсивные детали, связанные с повышенными частотами. С помощью высокочастотного фильтра можно так видоизменить изображение, чтобы скачки яркости на контурах будут сильно подчеркнуты, а в предельном случае вообще останутся только контуры. Ниже приведены примеры ядер высокочастотных фильтров.
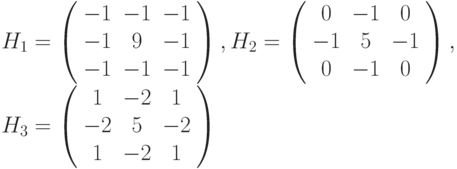
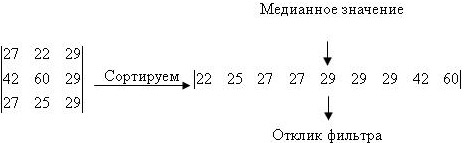
Медианный фильтр – пространственный процесс, который не подпадает под категорию свертки. Усредненное фильтрование использует значения элементов, содержащихся в области примыкания, для определения нового значения. Фильтр располагает элементы области примыкания в возрастающем порядке и отбирает среднее значение.
Результатом усредненного фильтра является то, что любой случайный шум, содержащийся в изображении, будет устранен. Это происходит потому, что любое случайное резкое изменение интенсивности элемента в пределах области примыкания, будет сортироваться, т.е. будет помещено либо в начало, либо в конец отсортированного списка.
Другим пространственным процессом, который можно продемонстрировать, используя свертку, является усиление края. В отличие от задачи обострения контуров (высокочастотный фильтр) здесь основной целью является не улучшение изображения, а наоборот, контуры должны быть отделены от всего изображения так, чтобы выходное изображение состояло только из контуров. Рассмотрим основные методы усиления края.
Метод усиления края по Лапласу не зависит от направления краев, и высвечиваются все направления. Ниже приведены три лапласиана.
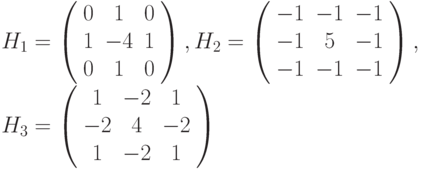
Метод усиления края с помощью оператора Собеля рассматривает два различных ядра свертки:
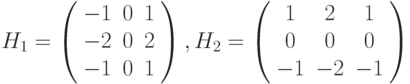
Исходя из этих сверток, вычисляется величина и направление краев. В качестве отклика данного фильтра выступает величина 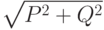 , где P и Q - отклики ядер
, где P и Q - отклики ядер 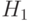 и
и 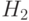 соответственно.
соответственно.
Метод усиления края с помощью оператора Превита также использует два ядра:
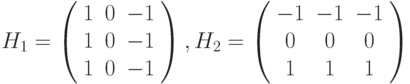
Результат работы оператора Превита есть max{P,Q}, где P и Q - отклики ядер 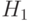 и
и 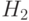 соответственно.
соответственно.
Метод преобразования реализующий эффект тиснения на изображении. Результирующее изображение выглядит как будто "выдавленным" или "вдавленным". Фильтр такого преобразования имеет вид:
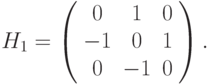
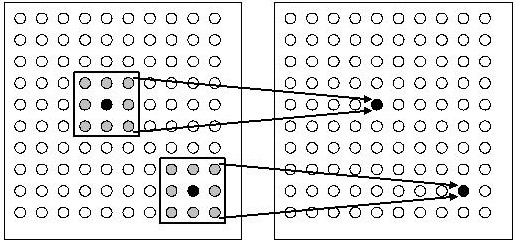
Как нам известно, обращение к элементам текстуры в пиксельном шейдере производится с помощью текстурных координат. Левый верхний тексель имеет текстурные координаты (0,0), левый нижний – координаты (0,1), правый верхний – координаты (1,0), правый нижний – координаты (1,1)
Задача состоит в том, чтобы для произвольного текселя изображения, имеющего текстурные координаты (u,v), определить значения текстурных координат восьми его соседей. Пусть у нас количество текселей в каждой строке будет W, а количество текселей в каждом столбце – H. В силу того, что тексели расположены равномерно (на одинаковом расстоянии друг от друга), можно вычислить шаг приращения du и dv в текстурных координатах по горизонтали и вертикали соответственно. Итак, 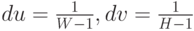 , где W и H – ширина и высота изображения соответственно. Например, для изображения, представленного выше, W = 20 пикселей, H = 9 пикселей, и шаг по горизонтали
, где W и H – ширина и высота изображения соответственно. Например, для изображения, представленного выше, W = 20 пикселей, H = 9 пикселей, и шаг по горизонтали 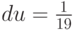 , а шаг по вертикали
, а шаг по вертикали 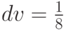 . Таким образом, для произвольного текселя, имеющего текстурные координаты (u,v), текстурные
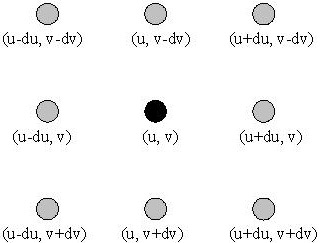
координаты его восьми соседей будут следующие: (u-du, v-dv), (u, v-dv), (u+du, v-dv), (u-du, v), (u+du, v), (u-du, v+dv), (u, v+dv), (u+du, v+dv), как показано на приведенном ниже рисунке.
. Таким образом, для произвольного текселя, имеющего текстурные координаты (u,v), текстурные
координаты его восьми соседей будут следующие: (u-du, v-dv), (u, v-dv), (u+du, v-dv), (u-du, v), (u+du, v), (u-du, v+dv), (u, v+dv), (u+du, v+dv), как показано на приведенном ниже рисунке.
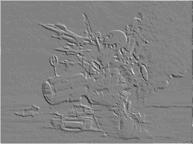
Ниже приведен пример пиксельного шейдера, который реализует метод усиления границ на изображении с помощью оператора Собеля и метод тиснения, а также примеры изображений.
sampler tex0;
struct PS_INPUT
{
float2 base : TEXCOORD0;
};
struct PS_OUTPUT
{
float4 diffuse : COLOR0;
};
PS_OUTPUT Main (PS_INPUT input)
{
PS_OUTPUT output;
const float W =320.0f;
const float H =240.0f;
const float du=1.0f/(W-1);
const float dv=1.0f/(H-1);
const float2 c[9] = {
float2(-du, -dv), float2(0.0f, -dv), float2(du, -dv),
float2(-du, 0.0f), float2(0.0f, 0.0f), float2(du, 0.0f),
float2(-du, dv), float2(0.0f, dv), float2(du, dv)
};
float3 col[9];
for (int i=0; i<9; i++) {
col[i] = tex2D(tex0, input.base+c[i]);
}
float lum[9];
float3 gray = (0.30f, 0.59f, 0.11f) ;
for (int i=0; i<9; i++) {
lum[i] = dot(col[i], gray);
}
float res1 = 0.0f;
float res2 = 0.0f;
const float sobel1[9] = { 1, 2, 1, 0, 0, 0, -1, -2, -1};
const float sobel2[9] = {-1, 0, 1, -2, 0, 2, -1, 0, 1};
const float tisnenie[9] = {0, 1, 0, -1, 0, 1, 0, -1, 0};
for (int i=0; i<9; i++) {
res1+=lum[i]*sobel1[i];
res2+=lum[i]*sobel2[i];
res+=lum[i]*tisnenie[i];
}
output.diffuse = sqrt(res1*res1+res2*res2);
//output.diffuse = res+0.5f;
return output;
};
6.1.