|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Доходность и риск
5.3. Ожидаемая доходность основных финансовых инструментов
Эффективное управление капиталом предполагает способность менеджера не только рассчитывать фактические показатели по уже совершенным операциям, но и (прежде всего) прогнозировать результаты будущих, планируемых финансовых операций. Ориентиром для такого прогнозирования являются будущие денежные потоки, возникновение которых ожидается от того либо иного способа инвестирования или привлечения капитала. Основными финансовыми инструментами осуществления капиталовложений или получения нового капитала являются ценные бумаги, прежде всего акции и облигации. Умение правильно определять ожидаемую доходность этих инструментов является необходимым условием выработки и обоснования эффективных управленческих решений.
Облигации являются более "предсказуемым" инструментом, так как в большинстве случаев по ним выплачивается фиксированный доход. Это облегчает планирование будущих денежных потоков и расчет ожидаемой доходности облигаций. В самом общем случае владение облигацией может принести два вида дохода – текущий в виде ежегодных купонных выплат и капитализированный, возникающий в результате превышения выкупной стоимости над ценой приобретения инструмента. Облигации, приносящие оба этих дохода называются купонными. По ним могут быть рассчитаны несколько показателей доходности. Одним из них является купонная доходность (ставка), определяемая отношением величины годового купона к номинальной (нарицательной) стоимости облигации:
 |
( 5.3.1) |
 – сумма годового купона;
– сумма годового купона;
 – номинальная стоимость облигации.
– номинальная стоимость облигации.
Например, по облигации номиналом 5 тыс. рублей предполагается ежегодно выплачивать купонный доход в сумме 1 тыс. рублей. В этом случае купонная ставка составит 20% годовых (1 / 5). Данный показатель очень далек от реальной доходности владения облигацией, так как во-первых, он учитывает только один вид дохода (купонные выплаты), а во-вторых, в знаменателе формулы показываются не фактические начальные инвестиции (цена покупки), а номинал облигации, то есть сумма долга, подлежащая возврату. Купонная ставка объявляется в момент эмиссии облигаций и служит для определения абсолютной суммы купонных выплат в рублях. Например, в объявлении о размещении займа сообщается, что по облигации номиналом 10 тыс. рублей установлена купонная ставка 18%. Это означает, что ежегодно владельцу одной облигации будет выплачиваться купонный доход в сумме 1,8 тыс. рублей (10 * 0,18).
Более приближенным к реальности является показатель текущей доходности, определяемый как отношение годовой купонной выплаты к цене покупки облигации:
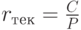 |
( 5.3.2) |
где  – цена приобретения облигации (сумма первоначальных инвестиций).
– цена приобретения облигации (сумма первоначальных инвестиций).
Например, если тысячерублевая облигация с ежегодным купоном 20% была приобретена за 925 рублей, то ее текущая годовая доходность составит 21,62% (200 / 925). Отличие от купонной ставки заключается в более точном учете первоначальных инвестиций. Однако текущей доходности присущ другой недостаток предыдущего показателя – она не отражает капитализированной доходности. Поэтому она также не может использоваться для сравнения эффективности различных инвестиций.
Строго говоря, оба рассмотренных выше показателя обладают еще одним недостатком – они не учитывают влияния на доходность количества купонных выплат в течение года. Как правило, эти выплаты производятся 2 раза в год. Держатель облигации получает возможность реинвестирования суммы купона за первое полугодие. Поэтому выплата по 500 рублей за каждые 6 месяцев выгоднее ему, чем разовая выплата 1000 рублей в конце года. Казалось бы, данное отличие легко учесть, введя в расчеты параметр  – число начислений процентов в году. На практике этого не делается – в числителях формул расчета текущей и купонной доходности отражается общая сумма купонных выплат за год. С одной стороны это позволяет избежать путаницы, а с другой – введение только одного дополнительного параметра не решает всей проблемы. На самом деле неоднократное в течение года
перечисление дохода порождает качественно новую задачу: вместо единичной выплаты возникает денежный поток. Поэтому использовать для него формулы начисления процентов на разовые платежи в принципе неверно. Чрезмерное усложнение математического аппарата в данном случае также неоправданно, принимая во внимание приблизительный характер самих показателей.
– число начислений процентов в году. На практике этого не делается – в числителях формул расчета текущей и купонной доходности отражается общая сумма купонных выплат за год. С одной стороны это позволяет избежать путаницы, а с другой – введение только одного дополнительного параметра не решает всей проблемы. На самом деле неоднократное в течение года
перечисление дохода порождает качественно новую задачу: вместо единичной выплаты возникает денежный поток. Поэтому использовать для него формулы начисления процентов на разовые платежи в принципе неверно. Чрезмерное усложнение математического аппарата в данном случае также неоправданно, принимая во внимание приблизительный характер самих показателей.
Наиболее совершенным показателем, в значительной мере свободным от трех названных выше недостатков, является средняя доходность за весь ожидаемый период владения облигацией. Для ее расчета используется качественно иной подход: вычисляется значение доходности к погашению (YTM) по методике, рассмотренной в предыдущем параграфе. Потенциальному инвестору в дополнение к уже известным данным (купон, номинал, цена покупки облигации) необходимо определиться со сроком, в течение которого он намерен владеть инструментом. Если этот период совпадает со сроком самой облигации, то он может рассчитывать на получение в конце срока суммы, равной номиналу. Иначе он должен спрогнозировать цену по которой облигация может быть продана в конце срока владения. В любом случае, проблема определения ожидаемой средней доходности облигации сведется для него к вычислению внутренней нормы доходности порождаемого ею денежного потока. Доход от прироста инвестиций будет отнесен к самой последней выплате в конце срока, то есть полученная величина будет отражать доходность к погашению.
Например, купонная трехлетняя облигация номиналом 3 тыс. рублей продается по курсу 92,5. Один раз в год по ней предусмотрена выплата купона в размере 750 рублей. Для того, чтобы определить YTM этого инструмента, инвестор должен сначала определить цену его покупки, перемножив курс на номинал: 3000 * 0,925 = 2775 рублей. Тогда поток платежей по облигации может быть представлен следующим числовым рядом: -2775, 750, 750, 3750. В соответствии с формулой (5.2.2) доходность к погашению представляет собой решение относительно YTM следующего уравнения:
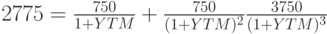
С помощью функции ВНДОХ на персональном компьютере можно вычислить 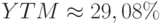 . В то же время купонная ставка составит лишь
. В то же время купонная ставка составит лишь  , а текущая доходность облигации
, а текущая доходность облигации 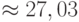 . В случае отсутствия под рукой компьютера или финансовых таблиц, можно применить упрощенную формулу расчета YTM (5.2.3):
. В случае отсутствия под рукой компьютера или финансовых таблиц, можно применить упрощенную формулу расчета YTM (5.2.3):

Предположим, инвестор не собирается держать облигацию в течение всего срока ее "жизни". В конце второго года он планирует продать ее за 2990 рублей. В этом случае денежный поток примет следующий вид: -2775, 750, 3740, а исходное уравнение для расчета YTM запишется в форме:
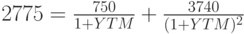
Внутренняя норма доходности этого потока (а следовательно – и YTM облигации) составит в этом случае 30,39%.
Аналогичная ситуация может возникнуть при наличии у эмитента права на досрочный выкуп (отзыв, call) облигации по фиксированной цене. В этом случае рассчитывается показатель доходности на момент отзыва (yield to call, YTC). Методика его расчета проиллюстрирована в предыдущем примере: вместо номинала облигации используется ее отзывная цена, а общий срок "жизни" инструмента заменяется числом лет, оставшихся до даты возможного выкупа. По такому же принципу рассчитывается ожидаемая полная доходность конвертируемых облигаций, которые через определенный период времени могут быть обменены (конвертированы) на обыкновенные акции предприятия-эмитента. Вместо отзывной цены в уравнении используется конверсионная стоимость облигации (PC), равная произведению ожидаемой рыночной цены обыкновенной акции на коэффициент конверсии (kC). Значение коэффициента конверсии устанавливается эмитентом при размещении займа. Спрогнозировать будущую рыночную цену обыкновенной акции, на которую может быть обменена облигация, должен сам инвестор.
В отличие от показателей купонной и текущей доходности, YTM реагирует на изменение числа купонных выплат в течение года. В случае, если это число превышает единицу, необходимо скорректировать ожидаемый денежный поток. Например, вместо одноразовой выплаты 750 рублей в год, эмитент решил выплачивать по 375 рублей каждое полугодие. В этом случае денежный поток будет иметь следующую структуру: -2775, 375, 375, 375, 375, 375, 3375. Соответственно, изменится уравнение для расчета YTM:
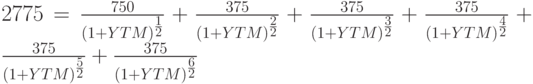
Доходность к погашению в этом случае составит 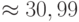 .
.
