Программные проекты на C#

Вычисление интеграла. Описание Решения (Solution) Integral

Задача вычисления значения определенного интеграла

Задача вычисления интеграла 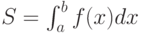также относится к классическим задачам математики и программирования. При рассмотрении параллельных вычислений в учебном курсе она достаточно подробно обсуждается. Вычисление интеграла аналогично задаче суммирования, поскольку практически вычисление значения S сводится к вычислению суммы .

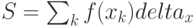Решение Integral содержит проекты, позволяющие провести сравнительный анализ эффективности последовательных и параллельных алгоритмов вычисления интеграла.

Структура Решения Integral

Решение Integral содержит 2 проекта. Следуя принципу разделения интерфейса и бизнес-логики, содержательная часть реализована в проекте ClassLibraryIntegral, представляющем динамическую библиотеку классов. Библиотека содержит один класс – Integral, включающий методы, реализующие последовательные и параллельные алгоритмы вычисления интеграла. Параллельный алгоритм построен на использовании инструментария Parallel.For.

Для распараллеливания используется стратегия сегментного алгоритма вычисления суммы. Интервал интегрирования разбивается на k сегментов, на каждом из которых для вычисления интеграла используется обычный последовательный алгоритм. Вычисление интегралов на отдельных сегментах ведется параллельно. Эта стратегия оказывается весьма эффективной, даже в том случае, когда вычисление интеграла на каждом сегменте ведется последовательно. Выигрыш по времени может достигать десятки раз при относительно небольшой потери точности. В учебном курсе поясняется причина такой эффективности. Подынтегральная функция на каждом участке ведет себя более гладко, в сравнении со всем интервалом интегрирования. По этой причине на каждом сегменте достаточно быстро достигается нужная точность вычислений.

Что касается последовательного метода вычисления интеграла на отрезке, то в классе Integral представлены два классических метода – более простой в реализации метод прямоугольников и более эффективный метод трапеций.

Интерфейсный проект – WindowsForm Integral представляет классическое Windows Form приложение, спроектированное для анализа двух проблем – анализа эффективности последовательного и параллельного алгоритма и анализа влияния числа сегментов на эффективность решения задачи.

Исследование ведется на примере подынтегральной функции, задающей гармонические колебания. Для интеграла от этой функции известно точное значение, что позволяет следить за точностью решения задачи. Интерфейс проекта позволяет легко менять параметры функции – амплитуду и частоту колебаний, также как и интервал интегрирования.

Задача вычисления интеграла. Результаты и Выводы

Рассмотрим результаты экспериментов по анализу сравнительной эффективности последовательного и параллельного алгоритмов в зависимости от числа сегментов разбиения интервала интегрирования:

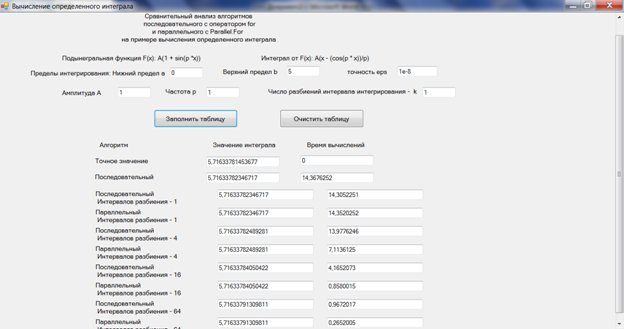
Рис. 9.5. Сравнительный анализ эффективности последовательного и параллельного алгоритмов (метод прямоугольников)

Анализируя эти результаты можно видеть, что интегрирование с разбиением на сегменты дает существенный выигрыш по времени. В данном эксперименте время сокращается в 15 раз при делении на 64 сегмента с 14, 4 секунды до 0, 97 секунды. Это ускорение достигается только за счет разделения на сегменты. Требуемая точность вычислений 10⁸ сохраняется.

Параллельный алгоритм выигрывает во всех случаях у последовательного алгоритма. За счет параллелизма достигается эффективное 4-х кратное ускорение, как и должно быть для компьютера с 4-мя ядрами.

Если вместо метода прямоугольников применять для вычисления интеграла значительно более эффективный метод трапеций, то при тех же данных последовательный алгоритм работает намного быстрее, поэтому и выиграть у него можно относительно немного. Вот каковы результаты эксперимента, когда в тех же условиях применяется более эффективный метод трапеций:

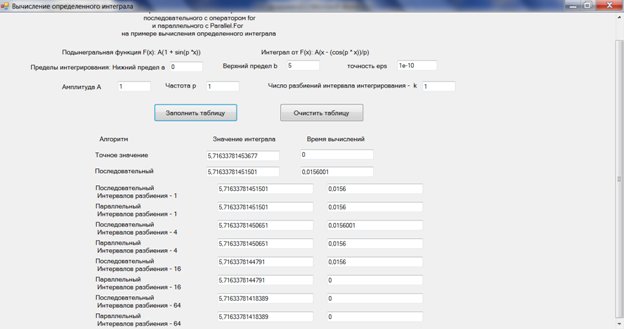
Рис. 9.6. Сравнительный анализ эффективности последовательного и параллельного алгоритмов (метод трапеций)

Анализируя эти результаты, можно видеть, что в данном случае последовательный алгоритм без разбиения интервала интегрирования на сегменты прекрасно справляется с задачей, затрачивая на решение 0, 015 секунды. Хотя параллельные алгоритмы работают не хуже, но говорить о реальном повышении эффективности вряд ли стоит.

Подводя итоги, можно сказать, что задача вычисления интеграла относится к задачам второго и третьего типа в зависимости от сложности вычисления подынтегральной функции. Когда подынтегральная функция вычислительно простая, как в нашем примере, то фактически задача вычисления интеграла имеет линейную сложность и относится ко второму типу, когда распараллеливание возможно, но не имеет особого смысла ввиду эффективной работы последовательного алгоритма. Для сложной в вычислительном отношении функции задачу следует относить к третьему типу и применять параллельные алгоритмы с разбиением интервала интегрирования на сегменты. Применение метода прямоугольников по существу имитирует увеличение сложности вычисления функции, демонстрируя, каков эффект можно получить при распараллеливании этой задачи.