Программные проекты на C#

Задача суммирования. Выводы

Начну с общих выводов, связанных с проблемой распараллеливания вычислений. Все задачи можно условно разделить на пять классов:

1. Нераспараллеливаемые задачи, носящие принципиально последовательный характер. Примером является сложная в вычислительном отношении задача о "Ханойской башне", по правилам которой перенос колец может осуществляться только последовательно.
2. Потенциально распараллеливаемые задачи, для которых распараллеливание неэффективно, поскольку последовательные алгоритмы работают быстрее, чем параллельные. Связано это с тем, что организация параллельных вычислений требует накладных расходов. Эти расходы могут съедать весь выигрыш, полученный за счет параллелизма в вычислениях. Как правило, к таким задачам относятся задачи с линейной временной сложностью.
3. Задачи, носящие принципиально параллельный характер, например сервер баз данных, параллельно обслуживающий многочисленные запросы. К этому же классу можно отнести потенциально распараллеливаемые задачи, для которых известны эффективно работающие параллельные алгоритмы.
4. Потенциально распараллеливаемые задачи, для которых разработка эффективно работающих параллельных алгоритмов является проблемой, требующей творческого подхода.
5. Частично распараллеливаемые задачи, в которых можно выделить не подлежащую распараллеливания часть задачи и часть, потенциально распараллеливаемую.

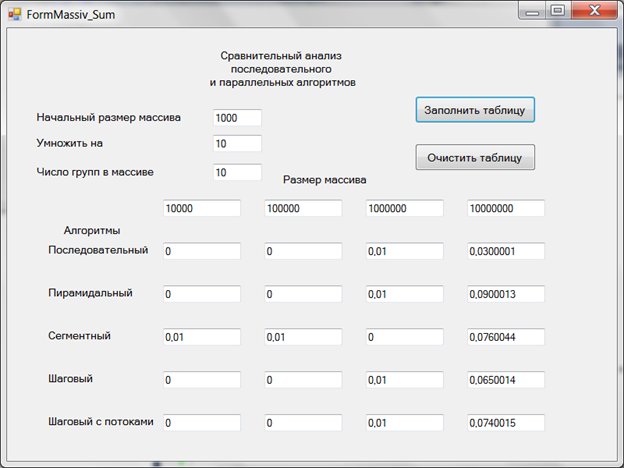
Что можно сказать о задаче суммирования? К какому из классов ее следует отнести? Начнем с задачи суммирования элементов массива. Прежде, чем дать ответ, рассмотрим результаты экспериментов по анализу сравнительной эффективности последовательного и различных параллельных алгоритмов по нахождению суммы элементов массивов различного размера, хранящих элементы вещественного типа (double). Вот какие результаты получены на моем компьютере (64-х битный компьютер с 6 Гб оперативной памяти и 4-мя физическими ядрами) при запуске Windows проекта из Решения Sum:

Рис. 9.1. Суммирование элементов массивов разного размера

Как можно видеть, все алгоритмы – последовательный и параллельные - прекрасно справляются с задачей. Время суммирования вплоть до массива, содержащего 10000000 -десять миллионов элементов, составляет менее 0,1 секунды. В такой ситуации параллельные алгоритмы не имеют преимущества перед последовательным алгоритмом. Так что задачу нахождения суммы элементов массива, также как нахождение максимального элемента и другие подобные ей задачи, следует отнести ко второму классу, где применение параллельных алгоритмов хотя и возможно, но нецелесообразно на компьютерах подобного класса.

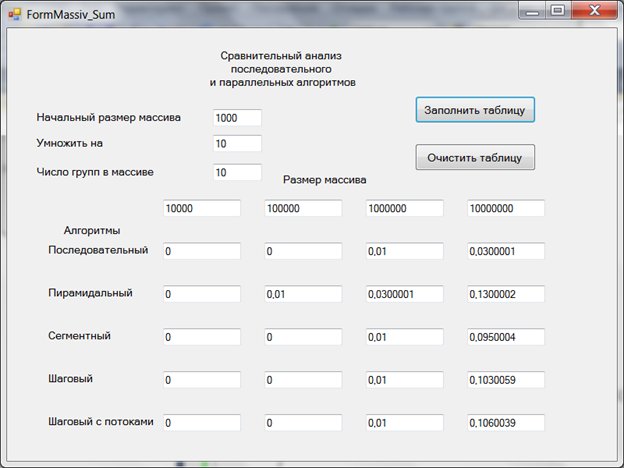
Хочу обратить внимание на одну особенность, связанную с результатами экспериментов. Время, замеряемое в экспериментах, содержит погрешности. Этих погрешностей избежать нельзя, поскольку они связаны с тем, как работает таймер в многозадачной операционной системе. Квант времени составляет 0,015 секунды, а ошибка измерения может достигать нескольких квантов. Для сравнения приведу результаты вычисления суммы элементов массива в тех же условиях, что и на рис. 1, но для другого сеанса работы:

Рис. 9.2. Суммирование элементов массива. Эксперимент 2

Как видите, результаты слегка отличаются от результатов первого эксперимента. Но замечу, что во всех случаях последовательный алгоритм выигрывает сотые доли секунды у любых параллельных алгоритмов на массиве из 10 миллионов элементов.

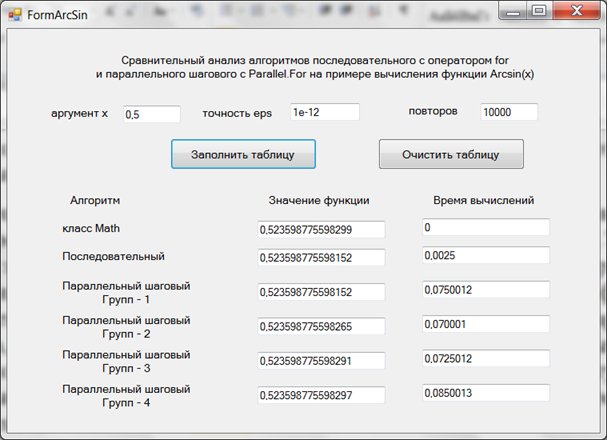
Приведу теперь результаты экспериментов для задачи суммирования бесконечного сходящегося ряда на примере вычисления значений функции Arcsin(x). Эта задача интересна еще и тем, что эффективный последовательный алгоритм использует рекуррентное соотношение для вычисления очередного члена суммы. При распараллеливании такого эффективного приема не существует. Рекуррентное соотношение хотя и можно построить для параллельного шагового алгоритма, но оно значительно сложнее в сравнении с последовательным вариантом. Учитывая еще, что последовательный алгоритм практически мгновенно решает эту задачу, то у параллельного алгоритма нет шансов выиграть, что и подтверждается результатами экспериментов:

Рис. 9.3. Суммирование сходящегося ряда

Можно видеть, что как последовательный, так и параллельный алгоритм прекрасно справляются с задачей. Время многократного (10000 повторов) вычисления значения функции менее 0,1 секунды. Но опять-таки параллельный алгоритм не имеет преимущества перед последовательным алгоритмом. Так что и эту задачу следует отнести ко второму классу, где применение параллельных алгоритмов хотя и возможно, но нецелесообразно на компьютерах подобного класса.

Полагаю, что справедлива следующая гипотеза:

Задачи с линейной временной сложностью относятся ко второму классу.

Для того чтобы параллельные алгоритмы выигрывали у последовательных алгоритмов исходная задача должно иметь по крайней мере квадратичную сложность. Суммирование конечного ряда, где каждый член ряда требует вычисления значения функции с линейной сложностью , относится к подобным задачам, поскольку для вычисления суммы ряда необходимо вычислить n членов ряда. Подробное описание примера приведено в 7-й главе учебника в разделе, посвященном методу Parallel.For, а его реализация представлена в классе Function_Sum. Вот как выглядят результаты эксперимента:

Рис. 9.4. Суммирование конечного ряда

Рассматриваемую нами задачу, имеющую квадратичную временную сложность 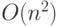следует отнести к третьему классу задач, допускающих эффективное распараллеливание. В главе 7 подробно обсуждается алгоритм, позволяющий перейти от исходной частично распараллеливаемой задачи к практически полному распараллеливанию. Анализируя приведенные результаты можно видеть, что последовательному алгоритму понадобилось ощутимо заметное время на вычисления – более 5 секунд. В то же время все параллельные алгоритмы выигрывают у последовательного алгоритма, лучший из них выигрывает более чем в 4 раза, что согласуется с числом ядер компьютера. Лучшим параллельным алгоритмом является алгоритм, построенный с использованием метода Parallel.For. Но и методы, использующие непосредственно потоки и объекты класса Task ведут себя вполне достойно на этой задаче.

Можно сделать и более общий вывод. Для потенциально распараллеливаемых задач со сложностью 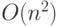и выше следует искать эффективные параллельные алгоритмы, позволяющие ощутимо сократить время решения задачи. Поиск таких алгоритмов непростая задача. Эта тема будет обсуждаться и при рассмотрении других проектов, дополняющих и сопровождающих учебник "Параллельные вычисления и многопоточное программирование".