Обработка и хранение информации
Развитие инструментальных средств обработки информации
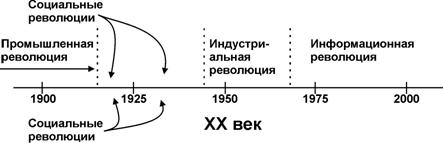
Без преувеличения можно сказать, что период между последней третью XIX и концом ХХ веков был "колыбелью" многих больших и малых революций ( рис. 2.6). Промышленная революция конца ХIХ - начала ХХ века и Первая мировая война породили волну социальных революций, которые если не перевернули, то основательно потрясли мировые устои.
Вторая мировая война и послевоенное развитие экономики, исследования в ядерной и микромолекулярной физике, электронике твердого тела и пограничных явлений, создание первых промышленных вычислительных устройств дали толчок индустриальной революции, которая за четверть века подготовила почву для бурного всплеска развития информационных технологий.
Качественные изменения, затронувшие последнюю часть прошлого столетия, имели под собой солидную многовековую историю. Вычислительная техника не сразу достигла современного уровня. В ее развитии отмечают предысторию и четыре поколения ЭВМ. Ниже приведены самые показательные факты предыстории.
Предыстория ЭВМ
Древнейшим счетным инструментом, который сама природа предоставила в распоряжение человека, была его собственная рука. Понятие числа и фигуры взято не откуда-то, а из действительного мира. "Десять пальцев, на которых люди учились считать (производить первую арифметическую операцию), представляют собой все что угодно, только не продукт свободного творческого разума" [http://www.junior.ru/wwwexam/history/frame.htm].
Имена числительные во многих языках указывают, что у первобытного человека орудием счета были преимущественно пальцы. Неслучайно в древнерусской нумерации единицы называются "перстами", десятки ¬- "составами", а все остальные числа - "сочинениями". Кисть же руки у многих народов называлась "пять". Например, малайское "лима" означает одновременно и "рука", и "пять".
От пальцевого счета берет начало пятеричная система счисления (одна рука), десятеричная (две руки), двадцатеричная (пальцы рук и ног). У многих народов пальцы рук остаются инструментом счета и на более высоких ступенях развития.
Хорошо был известен пальцевый счет в Риме. По свидетельству древнеримского историка Плиния-старшего, на главной римской площади Форуме была воздвигнута гигантская фигура двуликого бога Януса. Пальцами правой руки он изображал число 300, пальцами левой - 55. Вместе это составляло число дней в году в римском календаре.
В средневековой Европе полное описание пальцевого счета составил ирландец Беда Достопочтенный. Пальцевый счет сохранился кое-где и поныне. Историк и математик Л. Карпинский в книге "История арифметики" сообщает, что на крупнейшей мировой хлебной бирже в Чикаго предложения и запросы, как и цены, объявлялись маклерами на пальцах без единого слова.
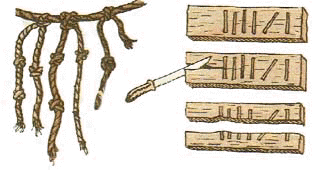
Издревле употребляется еще один вид инструментального счета - с помощью деревянных палочек с зарубками (бирок). В средние века бирками пользовались для учета и сбора налогов. Бирка разрезалась на две продольные части, одна оставалась у крестьянина, другая - у сборщика налогов. По зарубкам на обеих частях и велся счет уплаты налога, который проверяли складыванием частей бирки. В Англии, например, этот способ записи налогов существовал до конца XVII столетия. Другие народы - китайцы, персы, индийцы, перуанцы - использовали для представления чисел и счета ремни или веревки с узелками.
Бирки и веревки с узелками не могли удовлетворить возраставшие в связи с развитием торговли потребности в средствах вычисления. Развитию же письменного счета препятствовали два обстоятельства. Во-первых, не было подходящего материала для выполнения вычислений - глиняные и восковые таблички для этого не годились. Во-вторых, в тогдашних системах счисления письменно выполнить все необходимые операции было сложно. Этими обстоятельствами можно объяснить появление специального счетного прибора, известного в древности под именем абак.
Около 500 года нашей эры: изобретение абака.
Римский абак. Абаком называлась дощечка, покрытая слоем воска, на которой острой палочкой проводились линии и какие-нибудь фигуры, размещавшиеся в полученных колонках по позиционному принципу.
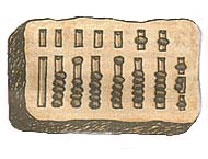
В Древнем Риме абак появился, вероятно, в V-VI вв н. э. и назывался calculi или abakuli. Изготовлялся он из бронзы, камня, слоновой кости и цветного стекла. До нашего времени дошел бронзовый римский абак, на котором камешки передвигались в вертикально прорезанных желобках. Внизу помещались камешки для счета до пяти, а в верхней части имелось отделение для камешка, соответствующего пятерке.
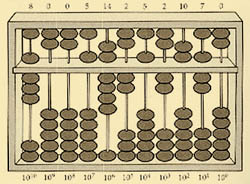
Суаньпань. Китайская разновидность абака (суаньпань) - появилась в VI веке н. э.; современный тип этого счетного прибора был создан позднее, по-видимому в XII столетии. Суаньпань представляет собой прямоугольную раму, в которой параллельно друг другу протянуты проволоки или веревки числом от девяти и более; перпендикулярно этому направлению суаньпань перегорожен на две неравные части. В большом отделении ("земля") на каждой проволоке нанизано по пять шариков, в меньшем ("небо") - по два. Проволоки соответствуют десятичным разрядам. Из рисунка видно, что суаньпань является практически точным аналогом инструмента "конторские счеты".
Соробан - японский абак, происходит от китайского суаньпаня, который был завезен в Японию в XV-XVI веках. Соробан проще своего предшественника, у него на "небе" на один шарик меньше, чем у суаньпаня.
Дощаный счет. Десятичный строй - довольно веское основание для того, чтобы признать временем возникновения этого прибора XVI век, когда десятичный принцип счисления был впервые применен в денежном деле в России. В это время какому-то наблюдательному человеку пришла в голову мысль заменить горизонтальные линии счета горизонтально натянутыми веревками, навесив на них, по существу, все те же "косточки-шарики".
Впрочем, в XVI веке термина "счеты" еще не существовало, и прибор именовался "дощаным счетом". Один из ранних образцов такого "счета" представлял собой два соединенных ящика, одинаково разделенных по высоте перегородками. В каждом ящике - два счетных поля с натянутыми веревками или проволочками. На верхних 10 веревках по 9 косточек (четок), на 11-й их - четыре, на остальных веревках - по одной.
Рассмотренные выше устройства (приборы) были предназначены для удобства использования и реализовывали в первую очередь наглядность счета. Расширился диапазон чисел, с которыми можно было производить простые арифметические действия. Однако механические вычислительные устройства и математические методы, предназначенные для ускорения процесса счета и его частичной автоматизации, появились лишь в XVII веке.
Вычислительные устройства
1614-й. Изобретение логарифмов шотландцем Джоном Непером. Вначале были составлены таблицы логарифмов, а затем, после смерти Непера, была изобретена логарифмическая линейка.
1642-й. Француз Блэз Паскаль изобрел и построил суммирующую машину - прототип арифмометра. В этой машине каждому десятичному разряду соответствовало колесико с нанесенными на него делениями от 0 до 9. Соседние колесики были механически связаны так, что избыток над 9 колесико передавало следующему, поворачивая его на 1. Этот прибор, практически без изменений, просуществовал и был в использовании более трех столетий!
1814-й. Англичанин Чарльз Бэббидж изобрел разностную машину, предназначенную для расчета и печати больших математических таблиц. В 1822 году он же сконструировал аналитическую машину, производящую вычисления по набору инструкций, записанных на перфокартах.
1890-й. Американец Герман Холлерит построил статистический табулятор с целью ускорить обработку результатов переписи населения. Машина Холлерита имела большой успех, на ее основе было создано преуспевающее предприятие, которое в 1924 году превратилась в фирму IBM - крупнейшего производителя современной вычислительной техники.
1936-й. Англичанин Алан Тьюринг опубликовал основополагающую работу "О вычислимых числах", заложив теоретические основы теории алгоритмов.