Математически эквивалентные преобразования
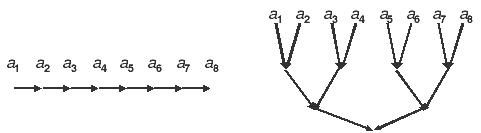
Аналогичные результаты и выводы имеют место, если суммирование чисел заменить их перемножением. В общем случае свойства обеих схем остаются такими же при любой ассоциативной операции, сколь бы сложной она не была. Например, если числа заменить квадратными матрицами одного порядка, а в качестве операции взять умножение матриц. Вычисления по второй схеме называются принципом " сдваивания " или принципом " разделяй и властвуй ". Обе схемы задают принципиально разные алгоритмы. Об этом говорит хотя бы тот факт, что их графы алгоритмов не изоморфны. Для случая n =8 они представлены на рис.5.1.
Глядя на эти графы легко понять, что реализация второй схемы предъявляет к организации коммуникаций значительно более жесткие требования, чем первая схема.
Как показывают примеры, на множестве математически эквивалентных преобразований имеет место большой разброс вычислительных свойств алгоритмов. Поэтому вполне естественно возникает вопрос о существовании преобразований, при которых те или иные свойства остаются без изменения, и критериях, гарантирующих сохранение соответствующих свойств. Рассмотрим один из критериев, связанный с сохранением наиболее важного вычислительного свойства, - влияния ошибок округления. Прежде чем переходить к конструктивным деталям, проведем некоторое предварительное обсуждение, которое поможет лучше понять, с чего и как надо начинать поиск критерия.
Математическое понятие алгоритма введено только для последовательных вычислений. Оно связывает множество выполняемых операций и порядок их реализации. Как было показано выше, любое изменение этого порядка, даже если оно соответствует математически эквивалентным преобразованиям, порождает другой алгоритм, у которого могут быть совершенно иные вычислительные свойства. Строгое понятие параллельного алгоритма не введено. Тем не менее, словосочетание "параллельный алгоритм" используется довольно широко и на практике, и в научных работах. На самом деле оно не означает ничего другого кроме как описание некоторой параллельной формы традиционного алгоритма. Наиболее часто словосочетание "параллельный алгоритм" связывается с другим словосочетанием "параллельная программа". Оно также не несет в себе никакого глубокого смысла и означает лишь то, что некоторый алгоритм записан в некоторой системе программирования, ориентированной на вычислительные системы параллельной архитектуры. При этом выделяются и описываются какие-то дополнительные структурные свойства алгоритма, связанные с параллелизмом. Как уже отмечалось, работа по поиску и оформлению этих дополнительных свойств возлагается на пользователя. Обычно за основу параллельной программы берется описание алгоритма на последовательном языке. В интересах эффективности реализации параллельной программы или в силу каких-то предпочтений в ее написании довольно часто делаются перестановки операций, замена одних операций другими, какие-то математически эквивалентные преобразования т.п. Еще раз подчеркнем, что все это может привести к изменению вычислительных свойств, которыми будет обладать записанный в виде программы алгоритм по сравнению со свойствами исходного алгоритма.
В вычислительной практике нередко смешиваются такие вроде бы похожие понятия как задача, метод, алгоритм и программа. Терминологическая нечеткость может приводить к серьезным ошибкам, поскольку при этом размываются различия между данными понятиями и, как следствие, не акцентируется внимание на возможных изменениях вычислительных свойств. На самом деле различия между ними можно описать достаточно четко. При этом каждое следующее понятие в цепочке задача - метод - алгоритм - программа будет в каком-то смысле уточнять предыдущее.
Задача: модель изучаемого явления формулируется в виде некоторой совокупности математических соотношений. Соотношения определяются в процессе постановки задачи и влияют на эффективность будущего вычислительного процесса лишь в той мере, в какой существуют для них эффективные методы нахождения общего решения.
Метод: для выбранной совокупности математических соотношений определяются общие контуры вычислений, включая множество выполняемых операций и схему связей между ними. На этапе выбора метода свойства вычислительного процесса определены во многом, но еще не полностью.
Алгоритм: в допустимых методом рамках точно определяются множество выполняемых операций и порядок их выполнения. Никакие изменения в дальнейшем, в том числе математически эквивалентные, не допускаются без проверки их влияния на вычислительные свойства.
Программа: алгоритм записывается на языке программирования с точным сохранением выбранного множества операций и порядка их выполнения. Никакие изменения, в том числе математически эквивалентные, не допускаются без проверки их влияния на вычислительные свойства. Если программа написана на каком-то параллельном языке, то при этом могут указываться некоторые дополнительные характеристики алгоритма. Такое указание не связано с преобразованием алгоритма. Оно лишь говорит о том, каким параллельным формам следует отдать предпочтение при реализации алгоритма.
Каждый численный метод порождает бесконечно большое множество математически эквивалентных алгоритмов и программ за счет математически эквивалентных формульных преобразований. Все они при одних и тех же входных данных дают одни и те же результаты только в тех случаях, когда все операции выполняются точно. Однако на данном множестве имеется огромный разброс вычислительных свойств, таких как общее число выполняемых операций, влияние ошибок округления, число параллельных ветвей вычислений, размер требуемой памяти, сложность коммуникационных связей и многих других. Важно подчеркнуть, что наличие одних хороших свойств у алгоритма или программы не гарантирует, что хорошими также будут и какие-то другие свойства.
Чтобы не потерять никакие свойства алгоритма, исследовать его, также как и реализовывать, можно только через формализованные описания. Других возможностей нет. Наиболее точными и, к тому же, наиболее распространенными формами описания являются математические соотношения и программы на последовательных языках. Чтобы найти не зависящие от форм записи инварианты алгоритмов и сопровождающие их критерии, необходимо максимально освободиться в самих записях от всего того, что не оказывает влияние на конечный результат. В первую очередь от таких особенностей языков описания как излишние ограничения на порядок выполнения операций, правила оформления записей, пересчет содержимого ячеек памяти и т.п. Что же остается после подобной чистки, если зафиксировать входные данные алгоритма? Остается ориентированный ациклический граф. Вершины графа символизируют выполняемые операции алгоритма. Из вершины А дуга идет в вершину В только тогда, когда операция, соответствующая вершине А, порождает результат, используемый в качестве аргумента операцией, соответствующей вершине В. Использование в качестве аргументов входных данных дугами не отмечается. Построенный граф представляет информационное ядро алгоритма. Это ядро может меняться при изменении входных данных. Очевидно, что информационное ядро алгоритма является не чем иным как введенным ранее графом алгоритма.
Теперь можно описать критерий сохранения ошибок округления при выполнении математически эквивалентных преобразований. Имеет место очень важное
Утверждение [ 1 ] . Пусть фиксирован способ округления, в котором ошибки округлений зависят только от входных данных операций. Предположим, что алгоритмы выполняют одно и то же множество арифметических действий. Тогда с точностью до некоторых уточнений оказывается, что для того чтобы при одних и тех же входных данных алгоритмов влияние ошибок округления в них было одним и тем же, необходимо и достаточно, чтобы графы алгоритмов были изоморфны.
Но ведь это утверждение практически не известно и, конечно, очень редко принимается во внимание при разработке алгоритмов и программ! Неудивительно поэтому, что влияние ошибок округления часто оказывается непредсказуемым.
Вернемся снова к параллельным формам алгоритмов. Рассмотренные
примеры позволяют сделать один вывод, весьма важный в методологическом
отношении. Пусть с помощью бинарных или унарных операций вычисляется
значение некоторого выражения, существенным образом зависящего от п
переменных. Предположим, что имеется алгоритм высоты s, позволяющий
это выражение вычислить. В соответствии с канонической параллельной
формой алгоритма каждая операция любого яруса, кроме первого,
использует хотя бы в качестве одного аргумента результат выполнения
какой-нибудь операции, находящейся в предыдущем ярусе. Кроме этого, не
ограничивая общности, можно допустить, что каждый промежуточный
результат где-то используется. В противном случае при вычислении
выражения какие-то промежуточные результаты в действительности
окажутся лишними, так как не будут оказывать влияние на окончательный
результат. Этот конечный результат зависит от всех входных переменных
и число аргументов во всех операциях не более двух. Поэтому число
операций в каждом ярусе не более чем в два раза превышает число
операций в следующем ярусе. Следовательно, результат вычисления
выражения при s ярусах будет зависеть не более чем от 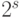 входных
данных. Отсюда вытекает, что
входных
данных. Отсюда вытекает, что  . Очевидно, что если для
вычисления выражения используются операции, имеющие не более p
аргументов, то
. Очевидно, что если для
вычисления выражения используются операции, имеющие не более p
аргументов, то 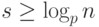 .
.
Таким образом, если какая-нибудь задача определяется n входными
данными, то нельзя рассчитывать в общем случае на существование
алгоритма ее решения с высотой меньше  . Если получен алгоритм
высоты порядка
. Если получен алгоритм
высоты порядка 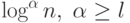 , то такой алгоритм можно считать
эффективным с точки зрения времени реализации на параллельной
вычислительной системе, если не принимать во внимание все другие
аспекты реализации. В частности, высота порядка
, то такой алгоритм можно считать
эффективным с точки зрения времени реализации на параллельной
вычислительной системе, если не принимать во внимание все другие
аспекты реализации. В частности, высота порядка  является оценкой
снизу для всех алгоритмов решения всех задач линейной алгебры с
матрицами порядка n. Для простейших задач линейной алгебры, таких как
умножение матрицы на вектор и перемножение двух матриц построены
алгоритмы, для которых нижние оценки высоты достигаются. Но для более
сложных задач подобные алгоритмы не найдены. Например, для задач
решения системы линейных алгебраических уравнений с квадратной
матрицей порядка n и обращения матрицы порядка n построены алгоритмы
высоты порядка
является оценкой
снизу для всех алгоритмов решения всех задач линейной алгебры с
матрицами порядка n. Для простейших задач линейной алгебры, таких как
умножение матрицы на вектор и перемножение двух матриц построены
алгоритмы, для которых нижние оценки высоты достигаются. Но для более
сложных задач подобные алгоритмы не найдены. Например, для задач
решения системы линейных алгебраических уравнений с квадратной
матрицей порядка n и обращения матрицы порядка n построены алгоритмы
высоты порядка 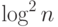 . Но не известно, существуют ли алгоритмы меньшей
высоты. Интересно отметить, что эти сверхбыстрые алгоритмы требуют для
своей реализации огромного числа процессоров порядка
. Но не известно, существуют ли алгоритмы меньшей
высоты. Интересно отметить, что эти сверхбыстрые алгоритмы требуют для
своей реализации огромного числа процессоров порядка 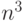 или
или 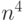 . И
снова не известно, существуют ли алгоритмы, требующие существенно
меньшего числа процессоров
[
1
]
.
. И
снова не известно, существуют ли алгоритмы, требующие существенно
меньшего числа процессоров
[
1
]
.
На заре развития параллельных вычислительных систем уделялось много внимания построению сверхбыстрых параллельных алгоритмов для задач с произвольными входными данными. Однако впоследствии интерес к ним заметно снизился, так как постепенно стало выясняться, что почти все они катастрофически неустойчивы, имеют сложные вычислительные схемы, требуют непомерно большого числа процессоров и очень много памяти, процессоры загружены крайне слабо и т.п. Единственными исключениями являются алгоритмы сдваивания для вычисления суммы или произведения n чисел. Эти алгоритмы применяются на практике достаточно часто. Почти все сверхбыстрые алгоритмы основаны на математически эквивалентных преобразованиях. Но все же хочется верить, что последнее слово в их исследовании еще не сказано. Ведь до сих пор очень мало что известно об алгоритмах, которые на множестве математически эквивалентных преобразований обеспечивают достижение тех или иных оптимальных вычислительных характеристик.