Характеристики вычислительных процессов
Большое число ФУ, также как и конвейерные ФУ, используются тогда, когда возникает потребность решить задачу быстрее. Чтобы понять, насколько быстрее это удается сделать, нужно ввести понятие "ускорение". Как и в случае загруженности, оно может вводиться различными способами, многообразие которых зависит от того, что с чем и как сравнивается. Нередко ускорение определяется, например, как отношение времени решения задачи на одном универсальном процессоре к времени решения той же задачи на системе из s таких же процессоров. Очевидно, что в наилучшей ситуации ускорение может достигать s. Отношение ускорения к s называется эффективностью. Заметим, что подобное определение ускорения применимо только к системам, состоящим из одинаковых устройств, и не распространяется на смешанные системы. Понятие же эффективности в рассматриваемом случае просто совпадает с понятием загруженности.
При введении понятия ускорения мы поступим иначе. Пусть алгоритм
реализуется за время Т на вычислительной системе из s устройств, в
общем случае простых или конвейерных и имеющих пиковые
производительности 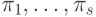 . Предположим, что
. Предположим, что  .
При реализации алгоритма система достигает реальной производительности r. Будем сравнивать скорость работы системы со скоростью работы
гипотетического простого универсального устройства, имеющего такую же
пиковую производительность
.
При реализации алгоритма система достигает реальной производительности r. Будем сравнивать скорость работы системы со скоростью работы
гипотетического простого универсального устройства, имеющего такую же
пиковую производительность 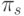 , как самое быстрое ФУ системы, и
обладающего возможностью выполнять те же операции, что все ФУ
системы.
, как самое быстрое ФУ системы, и
обладающего возможностью выполнять те же операции, что все ФУ
системы.
Итак, будем называть отношение  ускорением реализации
алгоритма на данной вычислительной системе или просто ускорением.
Выбор в качестве гипотетического простого, а не какого-нибудь другого,
например, конвейерного ФУ объясняется тем, что одно простое
универсальное ФУ может быть полностью загружено на любом алгоритме.
Теперь имеем
ускорением реализации
алгоритма на данной вычислительной системе или просто ускорением.
Выбор в качестве гипотетического простого, а не какого-нибудь другого,
например, конвейерного ФУ объясняется тем, что одно простое
универсальное ФУ может быть полностью загружено на любом алгоритме.
Теперь имеем

Подводя итог проведенным исследованиям, приведем для одного частного случая полезные выводы. Если система состоит из s простых или конвейерных устройств одинаковой пиковой производительности, то
- загруженность системы равна среднему арифметическому загруженностей всех устройств;
- реальная производительность системы равна сумме реальных производительностей всех устройств;
- пиковая производительность системы в s раз больше пиковой производительности одного устройства;
- обеспечиваемое системой ускорение равно сумме загруженностей всех устройств;
- если система состоит только из простых устройств, то ускорение равно отношению времени реализации алгоритма на одном универсальном простом устройстве с той же пиковой производительностью к времени реализации алгоритма на системе.
Пусть система устройств функционирует и показывает какую-то реальную производительность. Если производительность недостаточна, то для ее повышения необходимо увеличить загруженность системы. Для этого, в свою очередь, нужно повысить загруженность любого устройства, у которого она еще не равна 1. Но остается открытым вопрос, всегда ли это можно сделать. Если устройство загружено не полностью, то его загруженность заведомо можно повысить в том случае, когда данное устройство не связано с другими. В случае же связанности устройств ситуация не очевидна.
Снова рассмотрим систему из s устройств. Не ограничивая общности, будем считать все устройства простыми, так как любое конвейерное ФУ всегда можно представить как линейную цепочку простых устройств. Допустим, что между устройствами установлены направленные связи, и они не меняются в процессе функционирования системы. Построим ориентированный граф, в котором вершины символизируют устройства, а дуги - связи между ними. Дугу из одной вершины будем проводить в другую в том и только том случае, когда результат каждого срабатывания устройства, соответствующего первой вершине, обязательно передается в качестве аргумента для очередного срабатывания устройству, соответствующему второй вершине. Назовем этот граф графом системы. Не ограничивая существенно общности, можно считать его связным. Предположим, что каким-то образом в систему введены необходимые для начала работы данные. После запуска системы все ее функциональные устройства начинают работать под собственным управлением, соблюдая описанные выше правила.
Исследуем максимальную производительность системы, т.е. ее
максимально возможную реальную производительность при достаточно
большом времени функционирования. Пусть система состоит из s простых
устройств с пиковыми производительностями 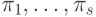 . Если граф
системы связный, то максимальная производительность
. Если граф
системы связный, то максимальная производительность  системы
выражается формулой
системы
выражается формулой

В самом деле, предположим, что дуга графа системы идет из i -го ФУ
в j -ое ФУ. Пусть за достаточно большое время i -ое ФУ выполнило  операций, j -ое ФУ -
операций, j -ое ФУ - 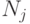 операций.
Каждый результат i -гo ФУ обязательно является одним из аргументов
очередного срабатывания j -го
ФУ. Поэтому количество операций, реализованных j -ым ФУ за время
операций.
Каждый результат i -гo ФУ обязательно является одним из аргументов
очередного срабатывания j -го
ФУ. Поэтому количество операций, реализованных j -ым ФУ за время  не
может более, чем на 1, отличаться от количества операций,
реализованных i -ым ФУ, т.е.
не
может более, чем на 1, отличаться от количества операций,
реализованных i -ым ФУ, т.е. 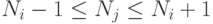 . Так как граф
системы связный, то любые две его вершины могут быть связаны цепью,
составленной из дуг. Допустим, что граф системы содержит q дуг. Если k -ое ФУ за время Т выполнило
. Так как граф
системы связный, то любые две его вершины могут быть связаны цепью,
составленной из дуг. Допустим, что граф системы содержит q дуг. Если k -ое ФУ за время Т выполнило  операций,
а l -ое ФУ -
операций,
а l -ое ФУ - 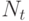 операций, то
из последних неравенств вытекает, что
операций, то
из последних неравенств вытекает, что  для любых
для любых  . Пусть устройства перенумерованы так, что
. Пусть устройства перенумерованы так, что  . Принимая во внимание эту упорядоченность и полученные для
числа выполняемых операций соотношения, находим, что
. Принимая во внимание эту упорядоченность и полученные для
числа выполняемых операций соотношения, находим, что
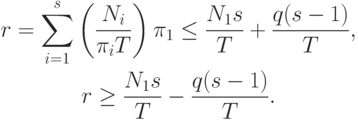
 , обязаны выполняться
неравенства
, обязаны выполняться
неравенства 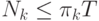 . В силу предполагаемой упорядоченности
производительностей
. В силу предполагаемой упорядоченности
производительностей 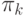 и того, что все
и того, что все  асимптотически равны между
собой, число операций, реализуемых каждым ФУ, будет асимптотически
максимальным, если выполняется равенство
асимптотически равны между
собой, число операций, реализуемых каждым ФУ, будет асимптотически
максимальным, если выполняется равенство  . Это означает, что
максимально возможная реальная производительность системы
асимптотически будет равна
. Это означает, что
максимально возможная реальная производительность системы
асимптотически будет равна 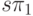 , что и требовалось доказать.
, что и требовалось доказать.Отметим несколько следствий. Пусть вычислительная система состоит
из s простых устройств с пиковыми производительностями 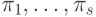 .
Если граф системы связный, то
.
Если граф системы связный, то
- асимптотически каждое из устройств выполняет одно и то же число операций;
- загруженность любого устройства не превосходит загруженности самого непроизводительного устройства;
- если загруженность какого-то устройства равна 1, то это - самое непроизводительное устройство;
- загруженность системы не превосходит
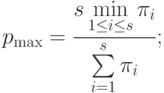
- ускорение системы не превосходит

Заметим, что равенство 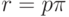 определяет многие узкие места
процесса функционирования системы. Некоторые описанные в литературе
узкие места связываются с именем Амдала, американского специалиста в
области вычислительной техники. Объявленные им законы легко выводятся
из полученных выше соотношений, поэтому мы не будем останавливаться на
их доказательствах. С деталями можно познакомиться в
[
1
]
. Чтобы не
терять узнаваемость различных фактов, мы будем оставлять именными
соответствующие утверждения, даже если они совсем простые. Возможно,
лишь несколько изменим формулировки, приспособив их к текущему
изложению материала.
определяет многие узкие места
процесса функционирования системы. Некоторые описанные в литературе
узкие места связываются с именем Амдала, американского специалиста в
области вычислительной техники. Объявленные им законы легко выводятся
из полученных выше соотношений, поэтому мы не будем останавливаться на
их доказательствах. С деталями можно познакомиться в
[
1
]
. Чтобы не
терять узнаваемость различных фактов, мы будем оставлять именными
соответствующие утверждения, даже если они совсем простые. Возможно,
лишь несколько изменим формулировки, приспособив их к текущему
изложению материала.
1-ый закон Амдала. Производительность вычислительной системы, состоящей из связанных между собой устройств, в общем случае определяется самым непроизводительным ее устройством.
Следствие. Пусть система состоит из простых устройств и граф системы связный. Асимптотическая производительность системы будет максимальной, если все устройства имеют одинаковые пиковые производительности.
Когда мы говорим о максимально возможной реальной производительности, то подразумеваем, что функционирование системы обеспечивается таким расписанием подачи команд, которое минимизирует простой устройств. Максимальная производительность может достигаться при разных режимах. В частности, она достигается при синхронном режиме с тактом, обратно пропорциональным производительности самого медленного из ФУ, если конечно, система состоит из простых устройств и граф системы связный. Пусть система состоит из s простых устройств одинаковой производительности. Тогда как в случае связанной системы, так и в случае не связанной, максимально возможная реальная производительность при больших временах функционирования оказывается одной и той же и равной s -кратной пиковой производительности одного устройства.
Мы уже неоднократно убеждались в том, что различные характеристики процесса функционирования системы становятся лучше, если система состоит из устройств одинаковой производительности. Предположим, что все устройства, к тому же, простые и универсальные, т. е. на них можно выполнять различные операции. Пусть на такой системе реализуется некоторый алгоритм, а сама реализация соответствует какой-то его параллельной форме. Допустим, что высота параллельной формы равна m, ширина равна q и всего в алгоритме выполняется N операций. В сформулированных условиях максимально возможное ускорение системы равно N/m.
Пусть система состоит из s устройств пиковой производительности  .
Предположим, что за время Т реализации алгоритма на i -ом ФУ
выполняется
.
Предположим, что за время Т реализации алгоритма на i -ом ФУ
выполняется  операций. По определению загруженность i -го ФУ равна
операций. По определению загруженность i -го ФУ равна 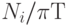 . Ускорение системы в данном случае равно
. Ускорение системы в данном случае равно
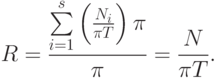
 Поэтому время Т реализации алгоритма не меньше, чем
Поэтому время Т реализации алгоритма не меньше, чем 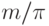 , и достигает этой величины, когда все ярусы реализуются
подряд без пропусков. Следовательно, ускорение системы при любом числе
устройств не будет превосходить N/m. Это означает, что минимальное
число устройств системы, при котором может быть достигнуто максимально
возможное ускорение, равно ширине алгоритма.
, и достигает этой величины, когда все ярусы реализуются
подряд без пропусков. Следовательно, ускорение системы при любом числе
устройств не будет превосходить N/m. Это означает, что минимальное
число устройств системы, при котором может быть достигнуто максимально
возможное ускорение, равно ширине алгоритма.Предположим, что по каким-либо причинам n операций из N мы
вынуждены выполнять последовательно. Причины могут быть разными.
Например, операции могут быть последовательно связаны информационно. И
тогда без изменения алгоритма их нельзя реализовать иначе. Но вполне
возможно, что мы просто не распознали параллелизм, имеющийся в той
части алгоритма, которая описывается этими операциями. Отношение  назовем долей последовательных вычислений.
назовем долей последовательных вычислений.
2-й закон Амдала. Пусть система состоит из s одинаковых простых универсальных устройств. Предположим, что при выполнении параллельной части алгоритма все s устройств загружены полностью. Тогда максимально возможное ускорение равно
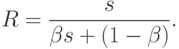
3-й закон Амдала. Пусть система состоит из простых одинаковых универсальных устройств. При любом режиме работы ее ускорение не может превзойти обратной величины доли последовательных вычислений.
В проведенных исследованиях нигде не конкретизировалось содержание операций. В общем случае они могут быть как элементарными типа сложения или умножения, так и очень крупными, представляющими алгоритмы решения достаточно сложных задач. Современные вычислительные системы состоят из десятков и даже сотен тысяч процессоров. Они вполне укладываются в рассмотренные модели. Системы с большим числом процессоров должны быть загружены достаточно полно. Проведенные исследования говорят о том, что в реализуемых на таких системах алгоритмах доля последовательных вычислений должна быть порядка десятых и сотых долей процента. Этот факт говорит о больших проблемах, которые должны сопровождать конструирование подобных алгоритмов.
В заключение еще раз подчеркнем следующее. В обширной литературе, посвященной параллельным процессам и параллельным вычислительным системам можно встретить много различных определений и законов, касающихся производительности, ускорения, эффективности и т. п. Как правило, новые определения и законы возникают тогда, когда старые в чем-то не устраивают исследователей. Однако ко всем таким "новациям" следует относиться очень осторожно. Довольно часто в попытке что-то "улучшить" скрываются какие-то узкие места, одни понятия подменяются другими, иногда просто проводятся ошибочные рассуждения, как, например, при сравнении достигаемых ускорений, исходя из законов Амдала и Густавсона-Барсиса [ 1 ] .
Уже отмечалось выше, что особенно много различных определений
дается для производительности системы. Приведем один курьезный пример.
Предположим, что система имеет два простых устройства одинаковой
пиковой производительности. Пусть одно устройство есть сумматор,
другое -умножитель. Допустим, что все обмены информацией
осуществляются мгновенно и решается задача вычисления матрицы 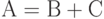 при заданных матрицах
при заданных матрицах  . Очевидно, что при естественном выполнении
операции сложения матриц реальная производительность будет равна
половине пиковой, так как умножитель не используется. Спрашивается:
"Можно ли каким-то образом на данной задаче повысить реальную
производительность?" Ответ: "Можно". Запишем равенство
. Очевидно, что при естественном выполнении
операции сложения матриц реальная производительность будет равна
половине пиковой, так как умножитель не используется. Спрашивается:
"Можно ли каким-то образом на данной задаче повысить реальную
производительность?" Ответ: "Можно". Запишем равенство 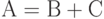 в виде
в виде 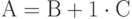 . Умножение элементов матрицы
. Умножение элементов матрицы  на 1
позволяет загрузить умножитель. Формально реальная производительность
увеличивается вдвое и сравнивается с пиковой.
на 1
позволяет загрузить умножитель. Формально реальная производительность
увеличивается вдвое и сравнивается с пиковой.
Вас интересует такое увеличение производительности?
