Вычислимые функции, тезис Тьюринга-Черча и неразрешимые проблемы
Частичная рекурсивность функций, вычислимых по Тьюрингу
В этом параграфе покажем, как можно промоделировать работу машины Тьюринга, используя частично рекурсивные определения.
Теорема 10.3. Всякая арифметическая функция, вычислимая на машинах Тьюринга, является частично рекурсивной функцией.
Доказательство этой теоремы - дополнительный материал, который можно при первом чтении опустить.
Доказательство Пусть м.Т. 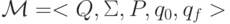 вычисляет функцию f(x1,..., xn).
Пусть также Q ={q0,q1,... ,q k-1 }, qf=q1 и
вычисляет функцию f(x1,..., xn).
Пусть также Q ={q0,q1,... ,q k-1 }, qf=q1 и 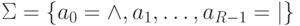 . Предположим также,
не ограничивая общности, что
. Предположим также,
не ограничивая общности, что 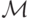 никогда не пишет пустой
символ
никогда не пишет пустой
символ  (как перестроить программу произвольной м.Т.,
чтобы она удовлетворяла этому условию ?).
(как перестроить программу произвольной м.Т.,
чтобы она удовлетворяла этому условию ?).
Определим кодирование элементов конфигураций 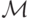 целыми числами. Пусть конфигурация
целыми числами. Пусть конфигурация  имеет вид K=(w1,qi,aj,w2), где
имеет вид K=(w1,qi,aj,w2), где 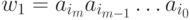 - слово на ленте левее головки, qi - состояние м.Т., aj - наблюдаемый в данной конфигурации символ
и w2= aj0aj1 ... ajp} - слово на ленте правее головки.
Кодом символа
- слово на ленте левее головки, qi - состояние м.Т., aj - наблюдаемый в данной конфигурации символ
и w2= aj0aj1 ... ajp} - слово на ленте правее головки.
Кодом символа  будет число j,
кодом состояния qi - число i.
Слова w1 и w2 будем рассматривать как числа в R -ичной
системе счисления, читаемые в противоположных направлениях (из наших
предположений следует, что
будет число j,
кодом состояния qi - число i.
Слова w1 и w2 будем рассматривать как числа в R -ичной
системе счисления, читаемые в противоположных направлениях (из наших
предположений следует, что  при m >0
и
при m >0
и 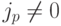 при p>0 ) :
при p>0 ) :
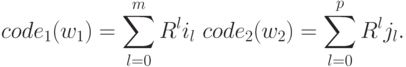
Например, если  , то для конфигурации K=(|**,q3,|,* | |) имеем code1(w1)=30 1+31 1+ 32 2= [211]3=22
и code2(w2)=30 1+ 31 2 +32 2= [221]3=25. По программе P определим следующие табличные функции, кодирующие ее команды:
, то для конфигурации K=(|**,q3,|,* | |) имеем code1(w1)=30 1+31 1+ 32 2= [211]3=22
и code2(w2)=30 1+ 31 2 +32 2= [221]3=25. По программе P определим следующие табличные функции, кодирующие ее команды:
A(i,j) - код символа, который пишет 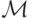 , когда она
в состоянии qi видит символ aj;
, когда она
в состоянии qi видит символ aj;
Q(i,j) - код состояния, в которое переходит 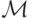 , когда
она в состоянии qi видит символ aj;
, когда
она в состоянии qi видит символ aj;
C(i,j) - код направления сдвига головки 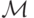 , когда
она в состоянии qi видит символ aj (0 - на месте, 1 - вправо, 2 - влево).
, когда
она в состоянии qi видит символ aj (0 - на месте, 1 - вправо, 2 - влево).
Пусть при i >= k или j >= R эти функции принимают какое-нибудь фиксированное значение (например, 0). Тогда по лемме 18.1 все они примитивно рекурсивны.
Определим функции, которые по кодам компонент одной конфигурации K=(w1,qi,aj,w2) вычисляют коды компонент следующей конфигурации K’=(w1’,qm,ap,w2’).
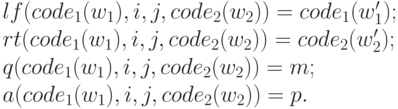
Покажем, что все эти функции примитивно рекурсивны. Для q это следует из того, что для любых i, j q(l,i,j,m)=Q(i,j). Определения остальных трех функций зависят от сдвига. При C(i,j)=0 имеем lf(l,i,j,r)=l, rt(l,i,j,r)= r, a(l,i,j,r)=A(i,j).
Если C(i,j)=2, то lf(l,i,j,r)=div(R, l), rt(l,i,j,r)= rR+A(i,j), a(l,i,j,r)=rm(R,l). Если же C(i,j)=1, то lf(l,i,j,r)=lR+A(i,j), rt(l,i,j,r)= div(R, r), a(l,i,j,r)=rm(R,r) Объединяя эти случаи получаем, что
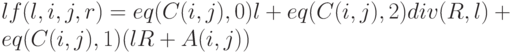
( здесь rm(x,y) - это функция, дающая остаток от деления y на x, а div(x,y) - функция целочисленного деления y на x ).
Аналогичные представления справедливы и для функций rt(l,i,j,r) и a(l,i,j,r). Следовательно, все эти функции примитивно рекурсивны.
Пусть из данной конфигурации K через t тактов получается конфигурация Kt. Определим коды компонент Kt как функции от компонент K и t :
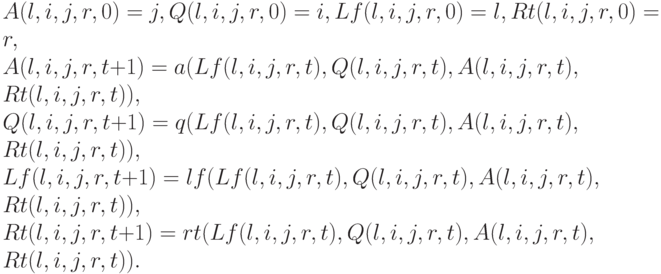
Это определение задает функции A(4), Q(4), Lf(4), Rt(4) с помощью совместной рекурсии. Следовательно, по лемме 18.5 они примитивно рекурсивны.
Пусть м.Т. 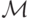 вычисляет функцию f(x), (т.е. n=1 ). Тогда для начальной конфигурации
вычисляет функцию f(x), (т.е. n=1 ). Тогда для начальной конфигурации  code1(w1)=0, code(q0)=0, code(|)=R-1, code2( w2 ) = (R-1)Rx-2+(R-1)R x-3+ ... +(R-1)R0=R x-1-1. Положим
code1(w1)=0, code(q0)=0, code(|)=R-1, code2( w2 ) = (R-1)Rx-2+(R-1)R x-3+ ... +(R-1)R0=R x-1-1. Положим 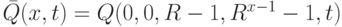 и
и 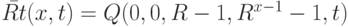 . Тогда функция
. Тогда функция  задает число шагов
до перехода
задает число шагов
до перехода 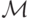 в заключительное состояние на входе x. Эта функция, очевидно, частично рекурсивна. Тогда функция
в заключительное состояние на входе x. Эта функция, очевидно, частично рекурсивна. Тогда функция 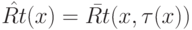 задает код правой
части заключительной конфигурации, имеющий вид Rf(x)-1-1.
Отсюда получаем, что
задает код правой
части заключительной конфигурации, имеющий вид Rf(x)-1-1.
Отсюда получаем, что
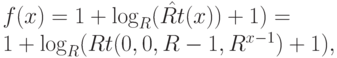
и следовательно, функция f(x) частично рекурсивна.
Тезис Тьюринга-Черча и алгоритмически неразрешимые проблемы
Мы рассмотрели три математические модели для описания алгоритмов и вычисляемых ими функций, отражающие различные аспекты и представления о работе абстрактного вычислителя. Из теорем 8.1, 10.2 и 10.3 непосредственно получаем
Следствие. Классы функций, вычислимых с помощью структурированных программ, машин Тьюринга и частично рекурсивных описаний, совпадают.
Естественно, возникает вопрос о том, насколько общим является этот результат? Верно ли, что каждый алгоритм может быть задан одним из рассмотренных способов? На эти вопросы теория алгоритмов отвечает следующей гипотезой.
Тезис Тьюринга-Черча:
Всякий алгоритм может быть задан в виде соответствующей машины Тьюринга или частично рекурсивного определения, а класс вычислимых функций совпадает с классом частично рекурсивных функций и с классом функций, вычислимых на машинах Тьюринга.
Значение этого тезиса заключается в том, что он уточняет общее неформальное определения "всякого алгоритма" и "вычислимой функции" через точные формальные понятия машины Тьюринга, частично рекурсивного определения и соответствующих им классов функций. После этого можно осмысленно ставить вопрос о существовании или несуществовании алгоритма, решающего тот или иной класс задач. Теперь этот вопрос следует понимать как вопрос о существовании или несуществовании соответствующей машины Тьюринга, или (что эквивалентно) структурированной программы, или частично рекурсивного определения соответствующей функции.
Можно ли доказать этот тезис как теорему? Нет, поскольку в его формулировке речь идет о неточных понятиях "всякого алгоритма" и "вычислимой функции", которые не могут быть объектами математических рассуждений. На чем же тогда основана уверенность в справедливости тезиса Тьюринга-Черча? В первую очередь, на опыте. Все известные алгоритмы, придуманные за многие века математиками, могут быть заданы с помощью машин Тьюринга. Для всех многочисленных моделей алгоритмов, появившихся за последние 70 лет (некоторые из них мы упоминали в начале лекции), была доказана их равносильность машинам Тьюринга. В качестве доводов в пользу тезиса Тьюринга-Черча можно также рассматривать замкнутость класса машин Тьюринга и ч.р.ф. относительно многочисленных естественных операций над алгоритмами и функциями. Отметим также, что тезис Тьюринга-Черча обращен и в будущее: он предполагает, что какие бы новые формальные определения алгоритмов ни были предложены (а таковыми, например, являются новые языки программирования), все они не выйдут из класса алгоритмов, задаваемых машинами Тьюринга.
Чтобы показать связь теории алгоритмов с "практическим" программированием, рассмотрим некоторые алгоритмичские проблемы, связанные со структурированными программами.
Зафиксируем конечный алфавит A={a0, a1,..., am-1}, включающий все символы латинского алфавита,
цифры, знак пробела (пусть это будет a0 ), знаки ' ; ', ' = ', ' < ', ' := ' , а также знаки-ключевые слова если, то, конец, пока, делай и все.
Тогда каждая структурированная программа  представляет собой некоторое слово
представляет собой некоторое слово 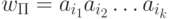 в алфавите A. Не ограничивая общности,
будем считать, что это слово начинается не с пробела, т.е. i1 >0.
Тогда слово
в алфавите A. Не ограничивая общности,
будем считать, что это слово начинается не с пробела, т.е. i1 >0.
Тогда слово 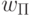 однозначно определяет натуральное число
однозначно определяет натуральное число  , m -ичной записью
которого оно является, т.е.
, m -ичной записью
которого оно является, т.е. 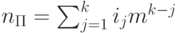 . Назовем это число
номером программы
. Назовем это число
номером программы  . По тексту программы
. По тексту программы  ее номер
ее номер  определяется однозначно.
Рассмотрим теперь обратное соответствие. Конечно, не каждое число является номером
некоторой структурированной программы. Поэтому сопоставим каждому числу
определяется однозначно.
Рассмотрим теперь обратное соответствие. Конечно, не каждое число является номером
некоторой структурированной программы. Поэтому сопоставим каждому числу 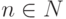 структурированную программу
структурированную программу 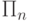 следующим образом:
если
следующим образом:
если  для некоторой программы
для некоторой программы 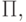 то
то 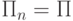 , иначе, т.е. когда n не является
"естественным" номером никакой программы, сопоставим ему в качестве
, иначе, т.е. когда n не является
"естественным" номером никакой программы, сопоставим ему в качестве 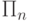 некоторую никогда не
останавливающуюся программу P (например, программу
некоторую никогда не
останавливающуюся программу P (например, программу 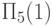 : x1 := x1; пока x1=x1 делай x1:=x1 все из примера 7.5).
: x1 := x1; пока x1=x1 делай x1:=x1 все из примера 7.5).
