Свойства замкнутости класса автоматных языков. Неавтоматные языки
Задачи
Задача 6.1. Примените процедуру детерминизации из теоремы 4.2 и постройте ДКА, эквивалентный построенному выше в примере 6.2 НКА M.
Задача 6.2. Цилиндрификация - это операция, которая обратна проекции.
Для любых алфавитов  и
и  таких, что
таких, что 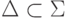 , и любого
языка L в алфавите
, и любого
языка L в алфавите  определим его цилиндрификацию
как язык
определим его цилиндрификацию
как язык  .
.
Показать, что для автоматного языка L язык 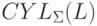 также является автоматным языком. Предложите процедуру перестройки автомата,
распознающего L , в автомат, распознающий
также является автоматным языком. Предложите процедуру перестройки автомата,
распознающего L , в автомат, распознающий 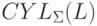 .
.
Задача 6.3.
Обращением слова 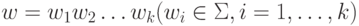 называется слово w{-1}= wk ... w2 w1. Показать, что для автоматного языка L его обращение - язык
называется слово w{-1}= wk ... w2 w1. Показать, что для автоматного языка L его обращение - язык 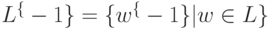 также является автоматным языком.
также является автоматным языком.
Задача 6.4.
Пусть L - автоматный язык в алфавите 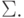 Доказать, что автоматными
являются и следующие языки:
Доказать, что автоматными
являются и следующие языки:
-
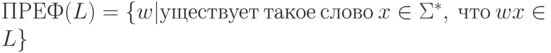 .
. -
 .
. -
 .
. -
 .
.
Задача 6.5. Пусть L - автоматный язык в алфавите 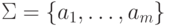 ,
а L1,..., Lm - это автоматные языки в алфавите
,
а L1,..., Lm - это автоматные языки в алфавите  Доказать, что автоматным является
и язык ЗАМ(L), полученный из слов L заменой каждой буквы ai на некоторое слово из Li, т.е.
Доказать, что автоматным является
и язык ЗАМ(L), полученный из слов L заменой каждой буквы ai на некоторое слово из Li, т.е.  и такие слова
и такие слова 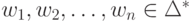 ,
что
,
что 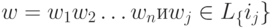 для всех j=1,2,... n }.
для всех j=1,2,... n }.
Задача 6.6. Пусть L - автоматный язык в алфавите 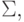 k - целое положительное число и
k - целое положительное число и  - отображение
- отображение 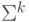 в
в 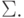 Доказать, что автоматным является язык
Доказать, что автоматным является язык 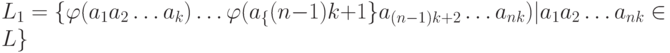 .
.
Задача 6.7. Докажите, что теорема 6.3 о разрастании остается справедливой и при замене условия 1) |xy| <= n на условие 1') |yz| <= n, т.е. повторяющееся подслово y имеется и в суффиксе w длины <= n.
Задача 6.8. Доказать, что следующие языки в алфавите 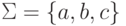 не являются автоматными.
не являются автоматными.
- Множество всех слов, в которых букв a на 3 больше, чем букв b.
- L={ ancbm | m > 3n }.
- L={ wcw-1 | w =a2bna для некоторого n > 0}.
- L={ w | |w| = 2n для некоторого целого числа n }.
-
 .
.
Задача 6.9.  -выражение - это либо
переменная x, или символ
-выражение - это либо
переменная x, или символ 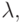 за которым следует переменная,
а далее либо
за которым следует переменная,
а далее либо  -выражение, либо левая скобка,
-выражение, либо левая скобка,  -выражение, еще одно
-выражение, еще одно  -выражение
и правая скобка.
Например,
-выражение
и правая скобка.
Например, 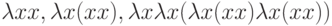 - это правильные
- это правильные  -выражения, а
-выражения, а 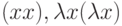 и
и 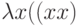 - неправильные.
Докажите, что язык
- неправильные.
Докажите, что язык  -выражений в алфавите
-выражений в алфавите  не является автоматным.
не является автоматным.
Задача 6.10. Выше в задаче строился автомат-распознаватель, который проверял правильность сложения двоичных чисел. Докажите, что для операции умножения двоичных чисел такого автомата не существует, т.е. что язык в алфавите троек битов U = {(x1(1),x2(1),y(1)) (x1(2),x2(2),y(2)) ... (x1(n),x2(n),y(n)) | y = y(n) ... y(2)y(1) - это первые n битов произведения двоичных чисел x1= x1(n)... x1(2)x1(1) и x2 = x2(n)... x2(2)x2(1)} не является автоматным.
Задача 6.11.
Доказать, что язык 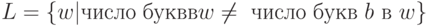 в алфавите
в алфавите 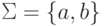 не является автоматным.
не является автоматным.
