Физические модели баз данных
Для файлов с постоянной длиной записи адрес размещения записи с номером K может быть вычислен по формуле:
ВА + (К- 1) * LZ + 1,
где ВА — базовый адрес, LZ — длина записи.
И как мы уже говорили ранее, если можно всегда определить адрес, на который -необходимо позиционировать механизм считывания-записи, то устройства прямого доступа делают это практически мгновенно, поэтому для таких файлов чтение произвольной записи практически не зависит от ее номера. Файлы прямого доступа обеспечивают наиболее быстрый доступ к произвольным записям, и их использование считается наиболее перспективным в системах баз данных.
На устройствах последовательного доступа могут быть организованы файлы только последовательного доступа.
Файлы с переменной длиной записи всегда являются файлами последовательного доступа. Они могут быть организованы двумя способами:
- Конец записи отличается специальным маркером.
- В начале каждой записи записывается ее длина.
Здесь LZN — длина N-й записи.
Файлы с прямым доступом обеспечивают наиболее быстрый способ доступа. Мы не всегда можем хранить информацию в виде файлов прямого доступа, но главное — это то, что доступ по номеру записи в базах данных весьма неэффективен. Чаще всего в базах данных необходим поиск по первичному или возможному ключам, иногда необходима выборка по внешним ключам, но во всех этих случаях мы знаем значение ключа, но не знаем номера записи, который соответствует этому ключу.
При организации файлов прямого доступа в некоторых очень редких случаях возможно построение функции, которая по значению ключа однозначно вычисляет адрес (номер записи файла).
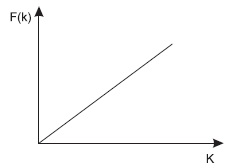
NZ = F(K),
где NZ — номер записи, K — значение ключа, F( ) — функция.
Функция F() при этом должна быть линейной, чтобы обеспечивать однозначное соответствие (см. рис. 9.5).
Однако далеко не всегда удается построить взаимно-однозначное соответствие между значениями ключа и номерами записей.
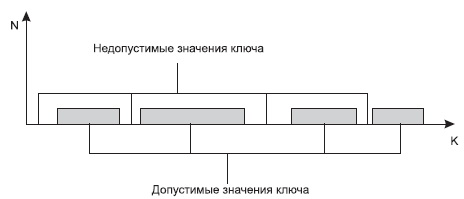
Часто бывает, что значения ключей разбросаны по нескольким диапазонам (см. рис. 9.6).
В этом случае не удается построить взаимно-однозначную функцию, либо эта функция будет иметь множество незадействованных значений, которые соответствуют недопустимым значениям ключа. В подобных случаях применяют различные методы хэширования (рандомизации) и создают специальные хэш- функции.
Суть методов хэширования состоит в том, что мы берем значения ключа ( или некоторые его характеристики) и используем его для начала поиска, то есть мы вычисляем некоторую хэш-функцию h(k) и полученное значение берем в качестве адреса начала поиска. То есть мы не требуем полного взаимно-однозначного соответствия, но, с другой стороны, для повышения скорости мы ограничиваем время этого поиска (количество дополнительных шагов) для окончательного получения адреса. Таким образом, мы допускаем, что нескольким разным ключам может соответствовать одно значение хэш-функции (то есть один адрес). Подобные ситуации называются коллизиями .Значения ключей, которые имеют одно и то же значение хэш-функции, называются синонимами.
Поэтому при использовании хэширования как метода доступа необходимо принять два независимых решения:
- выбрать хэш-функцию;
- выбрать метод разрешения коллизий.
Существует множество различных стратегий разрешения коллизий, но мы для примера рассмотрим две достаточно распространенные.
Стратегия разрешения коллизий с областью переполнения
Первая стратегия условно может быть названа стратегией с областью переполнения. При выборе этой стратегии область хранения разбивается на 2 части:
- основную область;
- область переполнения.
Для каждой новой записи вычисляется значение хэш-функции, которое определяет адрес ее расположения, и запись заносится в основную область в соответствии с полученным значением хэш-функции.
Основная область:
Область переполнения:
Если вновь заносимая запись имеет значение функции хэширования такое же, которое использовала другая запись, уже имеющаяся в БД, то новая запись заносится в область переполнения на первое свободное место, а в записи-синониме, которая находится в основной области, делается ссылка на адрес вновь размещенной записи в области переполнения. Если же уже существует ссылка в записи-синониме, которая расположена в основной области, то тогда новая запись получает дополнительную информацию в виде ссылки и уже в таком виде заносится в область переполнения.
При этом цепочка синонимов не разрывается, но мы не просматриваем ее до конца, чтобы расположить новую запись в конце цепочки синонимов, а располагаем всегда новую запись на второе место в цепочке синонимов, что существенно сокращает время размещения новой записи. При таком алгоритме время размещения любой новой записи составляет не более двух обращений к диску, с учетом того, что номер первой свободной записи в области переполнения хранится в виде системной переменной.
Рассмотрим теперь механизмы поиска произвольной записи и удаления записи для этой стратегии хэширования.
При поиске записи также сначала вычисляется значение ее хэш-функции и считывается первая запись в цепочке синонимов, которая расположена в основной области. Если искомая запись не соответствует первой в цепочке синонимов, то далее поиск происходит перемещением по цепочке синонимов, пока не будет обнаружена требуемая запись. Скорость поиска зависит от длины цепочки синонимов, поэтому качество хэш-функции определяется максимальной длиной цепочки синонимов. Хорошим результатом может считаться наличие не более 10 синонимов в цепочке.
При удалении произвольной записи сначала определяется ее место расположения. Если удаляемой является первая запись в цепочке синонимов, то после удаления на ее место в основной области заносится вторая (следующая) запись в цепочке синонимов, при этом все указатели (ссылки на синонимы) сохраняются.
Если же удаляемая запись находится в середине цепочки синонимов, то необходимо провести корректировку указателей: в записи, предшествующей удаляемой, в цепочке ставится указатель из удаляемой записи. Если это последняя запись в цепочке, то все равно механизм изменения указателей такой же, то есть в предшествующую запись заносится признак отсутствия следующей записи в цепочке, который ранее хранился в последней записи.