Арифметическое кодирование

Адаптивные алгоритмы сжатия. Кодирование Хаффмена

Является практичным, однопроходным, не требующим передачи таблицы кодов. Его суть в использовании адаптивного алгоритма, т.е. алгоритма, который при каждом сопоставлении символу кода, кроме того, изменяет внутренний ход вычислений так, что в следующий раз этому же символу может быть сопоставлен другой код, т.е. происходит адаптация алгоритма к поступающим для кодирования символам. При декодировании происходит аналогичный процесс.

В начале работы алгоритма дерево кодирования содержит только один специальный символ, всегда имеющий частоту 0. Он необходим для занесения в дерево новых символов: после него код символа передается непосредственно. Обычно такой символ называют escape-символом, <ESC>. Расширенный ASCII кодируют каждый символ 8-битным числом, т.е. числом от 0 до 255. При построении дерева кодирования необходимо для возможности правильного декодирования как-то упорядочивать структуру дерева. Расположим листья дерева в порядке возрастания частот и затем в порядке возрастания стандартных кодов символов. Узлы собираются слева направо без пропусков. Левые ветви помечаются 0, а правые - 1.

Рассмотрим процесс построения кодов по адаптивному алгоритму Хаффмена для сообщения ACCBCAAABC, которое соответствует выборке 10-и значений д.с.в. \[ X \] из 2-го примера на построение неадаптивного кода Хаффмена:

\[ % \smallskip \Treestyle{} \def\xbnth#1{\bnth{\raise2ex\hbox{#1}}} \noindent{\hbox{\vbox{\offinterlineskip \halign{\strut\vrule\ \hfil#\hfil\ \vrule&&\ \hfil#\hfil\ \vrule\cr \noalign{\hrule} входные& \lowrow{1.2}{код}& длина& \numsign\cr данные& & кода& №дерева\cr \noalign{\hrule} \omit\vrule height1pt\hfil\vrule& \omit\hfil\vrule& \omit\hfil\vrule& \omit\hfil\vrule\cr A& 'A'& 8& 1\cr C& 0'C'& 9& 2\cr C& 1& 1& 3\cr B& 00'B'& 10& 4\cr C& 1& 1& 5\cr A& 001& 3& 6\cr A& 01& 2& 7\cr A& 01& 2& 8\cr B& 001& 3& 9\cr C& 01& 2&\cr \noalign{\hrule}}}}% \]

\[ % \smallskip \Treestyle{\vdist{20pt}} \def\xbnth#1{\bnth{\raise2ex\hbox{#1}}} \beginTree%1 \node{\external\type{dot}\xbnth{0/\<ESC\>}} \node{\external\type{dot}\rght{1/A}} \node{\type{dot}\lft{1}} \endTree \setbox1=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%2 \node{\external\type{dot}\xbnth{0/\<ESC\>}} \node{\external\type{dot}\rght{1/A}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\rght{1/C}} \node{\type{dot}\lft{2}} \endTree \setbox2=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%3 \node{\external\type{dot}\xbnth{0/\<ESC\>}} \node{\external\type{dot}\rght{1/A}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\rght{2/C}} \node{\type{dot}\lft{3}} \endTree \setbox3=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%4 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/A}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{1/B}} \node{\type{dot}\lft{2}} \node{\external\type{dot}\xbnth{2/C}} \node{\type{dot}\lft{4}} \endTree \setbox4=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%5 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/A}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{1/B}} \node{\type{dot}\lft{2}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{5}} \endTree \setbox5=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%6 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{2/A}} \node{\type{dot}\lft{3}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{6}} \endTree \setbox6=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%7 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{3/A}} \node{\type{dot}\lft{4}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{7}} \endTree \setbox7=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%8 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{4}} \node{\external\type{dot}\xbnth{4/A}} \node{\type{dot}\lft{8}} \endTree \setbox8=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \beginTree%9 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 2/B.}} \node{\type{dot}\lft{2}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{5}} \node{\external\type{dot}\xbnth{4/A}} \node{\type{dot}\lft{9}} \endTree \setbox9=\hbox{\hskip\leftdist\unhbox\TeXTree\hskip\rightdist}% \ifdim\hsize>17mm\global\dzero24pt\else\dzero8pt\fi \lower\dzero\hbox{\ifdim\hsize>17mm\vbox{% \hbox{\hskip2.4em\box1\hskip1em\box2\hskip1em\box3\hskip1em\box4\hskip2em\box5}% \hbox{\hskip4em\box6\hskip2em\box7\hskip2em\box8\hskip2em\box9}% \hbox{\ }}\else \vbox{\hbox{\hskip5em\box1\hskip1em\box2}% \hbox{\hskip4em\box3\hskip1em\box4}\hbox{\ }}% \fi} \ifdim\hsize<175mm\smallskip \centerline{\box5\hskip4em\box6\hskip4em\box7} \smallskip \centerline{\box8\hskip6em\box9}\fi} \smallskip \]

Здесь L₁(ACCBCAAABC)=4.1 бит/сим. Если не использовать сжатия, то L₁(ACCBCAAABC)=8 бит/сим. Для рассматриваемой д.с.в. ранее были получены значения \[ ML_1(X)=1.6 \] бит/сим и \[ HX\approx1.523 \] бит/сим. С ростом длины сообщения среднее количество бит на символ сообщения при адаптивном алгоритме кодирования будет мало отличаться от значения, полученного при использовании неадаптивного метода Хаффмена или Шеннона-Фэно, т.к. алфавит символов ограничен и полный код каждого символа нужно передавать только один раз.

Теперь рассмотрим процесс декодирования сообщения 'A'0'C'100'B'1001010100101. Здесь и далее символ в апостофах означает восемь бит, представляющих собой запись двоичного числа, номера символа, в таблице ASCII+. В начале декодирования дерево Хаффмена содержит только escape-символ с частотой 0. С раскодированием каждого нового символа дерево заново перестраивается.

\[ \bigskip \centerline{\vbox{\offinterlineskip \halign{\strut\hfil\ #\ \hfil&&\vrule\hfil\ #\ \hfil\cr входные& \lowrow{1.2}{символ}& \numsign\cr данные& & № дерева\cr \noalign{\hrule} \omit\hfil& \omit\vrule height1pt\hfil& \omit\vrule\hfil\cr 'A' & A & 1\cr 0'C' & C & 2\cr 1 & C & 3\cr 00'B' & B & 4\cr ... & ... & ...\cr}}} \bigskip \]

Выбранный способ адаптации алгоритма очень неэффективный, т.к. после обработки каждого символа нужно перестраивать все дерево кодирования. Существуют гораздо менее трудоемкие способы, при которых не нужно перестраивать все дерево, а нужно лишь незначительно изменять.

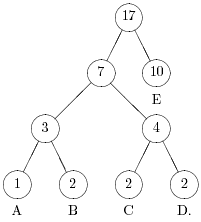
Бинарное дерево называется упорядоченным, если его узлы могут быть перечислены в порядке неубывания веса и в этом перечне узлы, имеющие общего родителя, должны находиться рядом, на одном ярусе. Причем перечисление должно идти по ярусам снизу-вверх и слева-направо в каждом ярусе.

На рис. 5.1 приведен пример упорядоченного дерева Хаффмена.

Рис. 5.1.

Если дерево кодирования упорядоченно, то при изменении веса существующего узла дерево не нужно целиком перестраивать - в нем достаточно лишь поменять местами два узла: узел, вес которого нарушил упорядоченность, и последний из следующих за ним узлов меньшего веса. После перемены мест узлов необходимо пересчитать веса всех их узлов-предков.

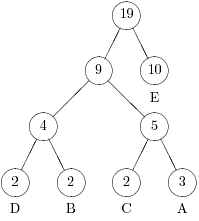
Например, если в дереве на рис. 5.1 добавить еще две буквы A, то узлы A и D должны поменяться местами (См. рис. 5.2).

Рис. 5.2.

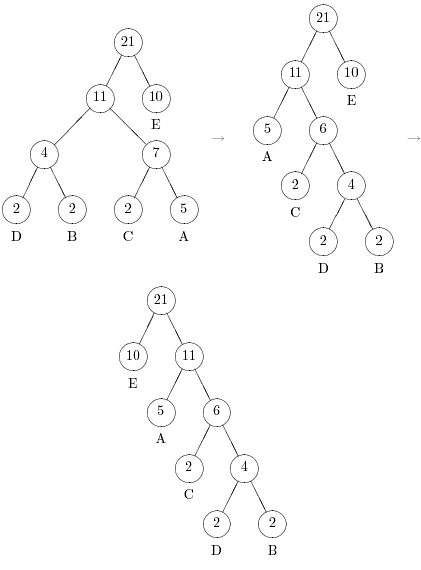
Если добавить еще две буквы A, то необходимо будет поменять местами сначала узел A и узел, родительский для узлов D и B, а затем узел E и узел-брат E (рис.5.3).

Рис. 5.3.

Дерево нужно перестраивать только при появлении в нем нового узла-листа. Вместо полной перестройки можно добавлять новый лист справа к листу <ESC> и упорядочивать, если необходимо, полученное таким образом дерево.

Процесс работы адаптивного алгоритма Хаффмена с упорядоченным деревом можно изобразить следующей схемой:

\[ \Treestyle{\vdist{20pt}} \noindent\hbox{\vbox{\offinterlineskip \halign{\strut\vrule\ \hfil#\hfil\ \vrule&&\ \hfil#\hfil\ \vrule\cr \noalign{\hrule} входные& \lowrow{1.2}{код}& длина& \numsign& метод\cr данные& & кода& дерева& получения\cr \noalign{\hrule} \omit\vrule height1pt\hfil\vrule& \omit\hfil\vrule& \omit\hfil\vrule& \omit\hfil\vrule& \omit\hfil\vrule\cr A& 'A'& 8& 1& добавление узла\cr C& 0'C'& 9& 2& добавление узла\cr C& 01& 2& 3& упорядочение\cr B& 00'B'& 10& 4& добавление узла\cr C& 1& 1& 5& не меняется\cr A& 01& 2& 6& не меняется\cr A& 01& 2& 7& упорядочение\cr A& 11& 2& 8& упорядочение\cr B& 101& 3& 9& не меняется\cr C& 11& 2&&\cr \noalign{\hrule}}}}% \beginTree%1 \node{\external\type{dot}\xbnth{0/\<ESC\>}} \node{\external\type{dot}\rght{1/A}} \node{\type{dot}\lft{1}} \endTree \setbox1=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%2 \node{\external\type{dot}\xbnth{0/\<ESC\>}} \node{\external\type{dot}\rght{1/C}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\rght{1/A}} \node{\type{dot}\lft{2}} \endTree \setbox2=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%3 \node{\external\type{dot}\xbnth{0/\<ESC\>}} \node{\external\type{dot}\rght{1/A}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\rght{2/C}} \node{\type{dot}\lft{3}} \endTree \setbox3=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%4 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{1/A}} \node{\type{dot}\lft{2}} \node{\external\type{dot}\xbnth{2/C}} \node{\type{dot}\lft{4}} \endTree \setbox4=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%5 \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{1/A}} \node{\type{dot}\lft{2}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{5}} \endTree \setbox5=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%6 \node{\external\type{dot}\xbnth{0/\<ESC\>}\ \ } \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{2/A}} \node{\type{dot}\lft{3}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{6}} \endTree \setbox6=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%7 \node{\external\type{dot}\xbnth{3/C}} \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{3/A}} \node{\type{dot}\lft{4}} \node{\type{dot}\lft{7}} \endTree \setbox7=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%8 \node{\external\type{dot}\xbnth{4/A}} \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 1/B}} \node{\type{dot}\lft{1}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{4}} \node{\type{dot}\lft{8}} \endTree \setbox8=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \beginTree%9 \node{\external\type{dot}\xbnth{4/A}} \node{\external\type{dot}\xbnth{0/\<ESC\>\ \ }} \node{\external\type{dot}\xbnth{\ \ 2/B.}} \node{\type{dot}\lft{2}} \node{\external\type{dot}\xbnth{3/C}} \node{\type{dot}\lft{5}} \node{\type{dot}\lft{9}} \endTree \setbox9=\hbox{\hskip\leftdist\box\TeXTree\hskip\rightdist}% \setbox10=\hbox{Здесь получится $L_1(\hbox{ACCBCAAABC})=4.1$ бит/сим.}% \ifdim\hsize>174mm% \lower6ex\hbox{\vbox{\hbox{\hskip2em\box1% \hskip1em\box2\hskip1em\box3\hskip1em\box4} \hbox{\hskip2em\box5\hskip2em\box6 \hskip2em\box7}% \hbox{\ }}} \vskip-5ex \centerline{\unhbox8\hskip4em\unhbox9 \lower9ex\hbox{\hskip5em\box10}} \else \raise2ex\hbox{\vbox{\hbox{\hskip4em\box1}\hbox{\hskip3em\box2}\hbox{\ }}} \smallskip \centerline{\unhbox3\hskip1em\unhbox4\hskip2em\unhbox5\hskip2em\unhbox6} \smallskip \centerline{\unhbox7\hskip2em\unhbox8\hskip2em\unhbox9} \smallskip \centerline{\box10}\fi \]

Упражнение 26 Закодировать сообщение BBCBBC, используя адаптивный алгоритм Хаффмена с упорядоченным деревом.

Упражнение 27 Закодировать сообщения "AABCDAACCCCDBB", "КИБЕРНЕТИКИ" и "СИНЯЯ СИНЕВА СИНИ", используя адаптивный алгоритм Хаффмена с упорядоченным деревом. Вычислить длины в битах исходного сообщения в коде ASCII+ и его полученного кода.

Упражнение 28 Распаковать сообщение 'A'0'F'00'X'0111110101011011110100101, полученное по адаптивному алгоритму Хаффмена с упорядоченным деревом, рассчитать длину кода сжатого и несжатого сообщения в битах.