3.1 Основные операторы языка программирования

Рассмотренные в предыдущих главах группы команд, состоящие из операторов присваивания и обращения к встроенным функциям, представляют собой простейшие программы Octave. Если такая программа хранится в файле с расширением .m (.M), то для её выполнения достаточно в командной строке Octave ввести имя этого файла (без расширения). В Octave встроен достаточно мощный язык программирования. Рассмотрим основные операторы этого языка и примеры их использования.

3.1.1 Оператор присваивания

Оператор присваивания служит для определения новой переменной (п. 2.4). Для того, чтобы определить новую переменную, достаточно присвоить ей значение: имя_переменной = значение_выражения

Любую переменную Octave воспринимает как матрицу. В простейшем случае матрица может состоять из одной строки и одного столбца:

	
>>> m=pi
m = 3.1416
>>> m
m = 3.1416
>>> m(1)
ans = 3.1416
>>> m(1, 1)
ans = 3.1416
>>> m(1, 2)
error : A(I): Index exceeds matrix dimension.
>>> m(3)
error : A(I): Index exceeds matrix dimension.
>>> M=e; M(3, 3)=e/2;
>>> M
M =
	2.71828 0.00000 0.00000
	0.00000 0.00000 0.00000
	0.00000 0.00000 1.35914

3.1.2 Организация простейшего ввода и вывода в диалоговом режиме

Даже при разработке простейших программ возникает необходимость ввода исходных данных и вывода результатов. Если для вывода результатов на экран можно просто не ставить ";" после оператора, то для ввода исходных данных при разработке программ, работающих в диалоговом режиме, следует использовать функцию

имя_переменной = input(’подсказка’);

Если в тексте программы встречается оператор input, то выполнение программы приостанавливается, Octave выводит на экран текст подсказки и переходит в режим ожидания ввода. Пользователь вводит с клавиатуры значение и нажимает клавишу Enter. Введённое пользователем значение будет присвоено переменной, имя которой указано слева от знака присваивания.

Для вывода результатов можно использовать функцию следующей структуры: disp(’строка_символов’) или disp(имя_переменной)

Пример 3.1. Создать программу для вычисления значения \[ y \] по формуле \[ y = sin(x) \] , при заданном значении \[ x \] .

Текст программы и результаты её работы показаны в листинге 3.1.

	
x=input (’Введите значение x=’); y=sin(x);
disp(’Значение y=’); disp(y);
% Результат работы программы
Введите значение x= pi/4
Значение y= 0.70711

3.1.3 Условный оператор

Одним из основных операторов, реализующим ветвление в большинстве языков программирования, является условный оператор. Существует обычная, сокращённая и расширенная формы этого оператора в языке программирования Octave.

Обычный условный оператор имеет вид:

	
if условие
	операторы_1
else
	операторы_2
end

Здесь условие — логическое выражение, операторы_1, операторы_2 — операторы языка или встроенные функции Octave. Обычный оператор if работает по следующем алгоритму: если условие истинно, то выполняются операторы_1, если ложно —операторы_2.

Пример 3.2. Даны вещественные числа \[ x \] и \[ y \] . Определить принадлежит ли точка с координатами \[ (x; y) \] заштрихованной части плоскости (рис. 3.1).

Как показано на рис. 3.1, фигура на плоскости ограничена линиями \[ x = -1, x = 3, y =-2 \] и \[ y = 4 \] . Значит точка с координатами \[ (x; y) \] будет принадлежать этой фигуре, если будут выполняться следующие условия: \[ x\ge-1,x\le3,y\ge-2 \] и \[ y\le4 \] . Иначе точка лежит за пределами фигуры.

Далее приведён текст программы и результаты её работы.

	
x=input (’x=’); y=input (’y=’);
if(x>= -1) & (x<=3) & (y>=-2) & (y<=4)
	disp ( ’Точка принадлежит фигуре’ )
else
	disp ( ’Точка не принадлежит фигуре’ );
end
% Результаты работы программы
x= 3
y= 3
Точка принадлежит фигуре
% ______________________________
x= 4
y= 4
Точка не принадлежит фигуре

Рис. 3.1. Графическое представление задачи из примера 3.2

Сокращённый условный оператор записывают так:

	
if условие
	операторы
end

Работает этот оператор следующим образом. Если условие истинно, то выполняются операторы, в противном случае управление передаётся оператору, следующему за оператором if :

	
z =0;
x=input(’x=’); y=input(’y=’);
if(x~=y)
	z=x+y;
end;
disp(’Значение Z=’); disp(z);
% Результаты работы программы
x= 3
y= 5
Значение Z= 8
x= 3
y= 3
Значение Z= 0

Расширенный условный оператор применяют когда одного условия для принятия решения недостаточно:

	
if  условие_1
	операторы_1
elseif  условие_2
	операторы_2
elseif условие_3
	операторы_3
. . .
elseif условие_n
	операторы_n
else
	операторы
end

Расширенный оператор if работает так. Если условие_1 истинно, то выполняются операторы_1, иначе проверяется условие_2, если оно истинно, то выполняются операторы_2, иначе проверяется условие_3 и т.д. Если ни одно из условий по веткам elseif не выполняется, то выполняются операторы по ветке else.

Рассмотрим использование расширенного условного оператора на примере.

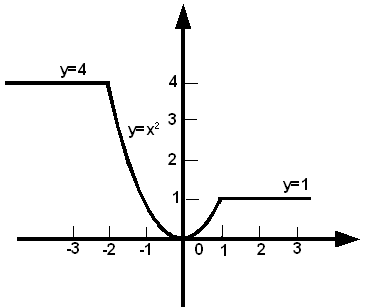
Пример 3.3. Дано вещественное число \[ x \] . Для функции, график которой приведён на рис. 3.2 вычислить \[ y = f (x) \] .

Аналитически функцию, представленную на рис. 3.2, можно записать так:

Составим словесный алгоритм решения этой задачи:

1. Начало алгоритма.
2. Ввод числа \[ x \] (аргумент функции).
3. Если значение \[ x \] меньше либо равно -2, то переход к п. 4, иначе переход к п. 5.
4. Вычисление значения функции: \[ y = 4 \] , переход к п. 8.
5. Если значение \[ x \] больше либо равно 1, то переход к п. 6, иначе переход к п. 7.
6. Вычисление значения функции: \[ y = 1 \] , переход к п. 8.
7. Вычисление значения функции: \[ y = x^2 \] .
8. Вывод значений аргумента \[ x \] и функции \[ y \] .
9. Конец алгоритма.

Рис. 3.2. Графическое представление задачи из примера 3.3

Текст программы будет иметь вид:

	
x=input(’x=’);
if x<= -2
	y=4;
elseif x>=1
	y=1;
else
	y=x ^2;
end;
disp(’y=’); disp(y);
% Результаты работы программы
x= 2
y= 1
% ______________________________
x= -3
y= 4
% ______________________________
x= 0.5
y= 0.25000