Введение.Основы генетических алгоритмов

1.2. Генетические операторы

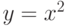Рассматриваемый ниже пример заимствован из популярной монографии Голдберга [3] и состоит в поиске целочисленного значения (для простоты) на отрезке от [0,31], при котором функции принимает максимальное значение.

Рис. 1.2. Пример функции

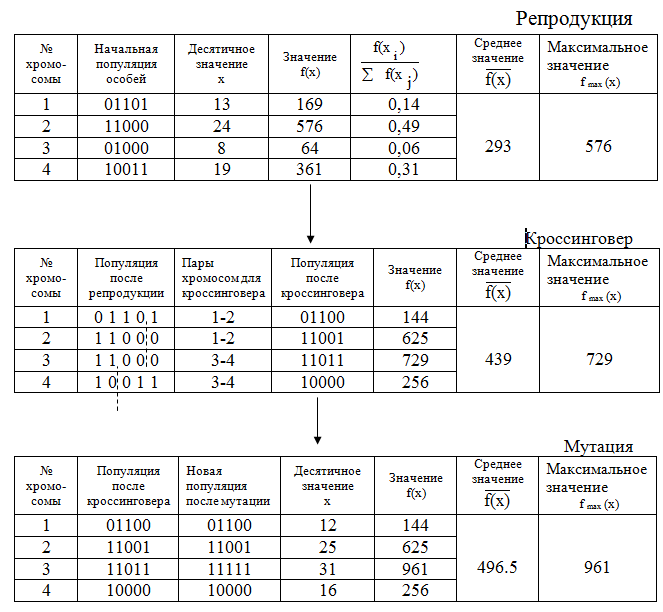
Начальный этап работы ГА для данного примера приведен в верхней таблице (репродукция) рис.1.3 Здесь особи начальной популяции (двоичные коды значений переменных - столбец 2) сгенерированы случайным образом. Двоичный код значения х называется хромосомой (она представляет генотип). Популяция образует множество потенциальных решений данной проблемы. В третьем столбце представлены их десятичные значения (фенотип). Далее на этом примере проиллюстрируем работу трех основных генетических операторов.

1.2.1. Репродукция

Репродукция – это процесс, в котором хромосомы копируются в промежуточную популяцию для дальнейшего "размножения" согласно их значениям целевой (фитнесс-) функции. При этом хромосомы с лучшими значениями целевой функции имеют большую вероятность попадания одного или более потомков в следующее поколение.

Очевидно, оператор репродукции (ОР) является искусственной версией естественной селекции – выживания сильнейших по Ч. Дарвину. Этот оператор представляется в алгоритмической форме различными способами (подробнее различные варианты ОР будут рассмотрены далее). Самый простой (и популярный) метод реализации ОР – построение колеса рулетки, в которой каждая хромосома имеет сектор, пропорциональный по площади значению ее целевой функции. Для нашего примера "колесо рулетки" имеет вид, представленный на рис.1.4.

Для селекции хромосом используется случайный поиск на основе колеса рулетки. При этом колесо рулетки вращается и после останова ее указатель определяет хромосому для селекции в промежуточную популяцию (родительский пул).

Рис. 1.3. Эволюция популяции

Очевидно, что хромосома, которой соответствует больший сектор рулетки, имеет большую вероятность попасть в следующее поколение. В результате выполнения оператора репродукции формируется промежуточная популяция, хромосомы которой будут использованы для построения поколения с помощью операторов скрещивания.

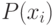В нашем примере выбираем хромосомы для промежуточной популяции, вращая колесо рулетки 4 раза, что соответствует мощности начальной популяции. Величину обозначим как , тогда ожидаемое количество копий i-ой хромосомы определяется значением , где N-мощность популяции. Число копий хромосомы, переходящих в следующее поколение, иногда определяется и так: , где - среднее значение хромосомы в популяции.

Рис. 1.4. Колесо рулетки

Расчетные числа копий хромосом по приведенной формуле следующие: хромосома 1 - 0,56; хромосома 2 - 1,97; хромосома 3 – 0,22; хромосома 4 – 1,23. В результате, в промежуточную популяцию 1-я хромосома попадает в одном экземпляре, 2-я – в двух, 3-я – совсем не попадает, 4-я – в одном экземпляре. Полученная промежуточная популяция является исходной для дальнейшего выполнения операторов кроссинговера и мутации.

1.2.2 Оператор кроссинговера (скрещивания)

Одноточечный или простой оператор кросинговера (ОК) с заданной вероятностью 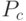выполняется в три этапа:

1-й этап. Две хромосомы (родители) выбираются случайно (или одним из методов, рассмотренных далее) из промежуточной популяции, сформированной при помощи оператора репродукции (ОР).

2-й этап. Случайно выбирается точка скрещивания - число из диапазона , где – длина хромосомы (число бит в двоичном коде).

Две новых хромосомы A', B' (потомки) формируются из A и B путем обмена подстрок после точки скрещивания:

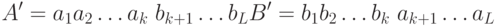
Например, рассмотрим выполнение кроссинговера для хромосом 1 и 2 из промежуточной популяции:

Следует отметить, что ОК выполняется с заданной вероятностью 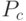(отобранные два родителя не обязательно производят потомков). Обычно величина вероятности полагается равной .

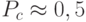Таким образом, операторы репродукции и скрещивания очень просты – они выполняют копирование особей и частичный обмен частей хромосом. Продолжение нашего примера представлено на рис.1.3 во второй таблице (кроссинговер).

Сравнение с предыдущей таблицей показывает, что в промежуточной популяции после скрещивания улучшились все показатели популяции (среднее и максимальное значения целевой функции - ЦФ).

1.2.3 Мутация

Далее согласно схеме классического ГА с заданной вероятностью выполняется оператор мутации. Иногда этот оператор играет вторичную роль. Обычно вероятность мутации мала -

Оператор мутации (ОМ) выполняется в два этапа:

1-й этап. В хромосоме случайным образом выбирается -ая позиция (бит) .

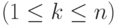2-й этап. Производится инверсия значения гена в -й позиции:

Например, для хромосомы 11011 выбирается и после инверсии значения третьего бита получается новая хромосома – 11111. Продолжение нашего примера представлено в третьей таблице (мутация) рис.1.3 образом, в результате применения генетических операторов найдено оптимальное решение .

В данном случае, поскольку пример искусственно подобран, мы нашли оптимальное решение за одну итерацию. В общем случае ГА работает до тех пор, пока не будет выполнен критерий окончания процесса поиска и в последнем полученном поколении определяется лучшая особь, которая и принимается в качестве решения задачи.