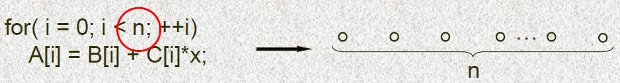Математические основы параллельных вычислений

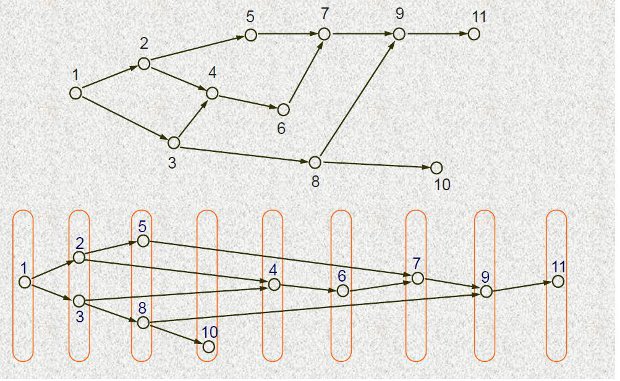
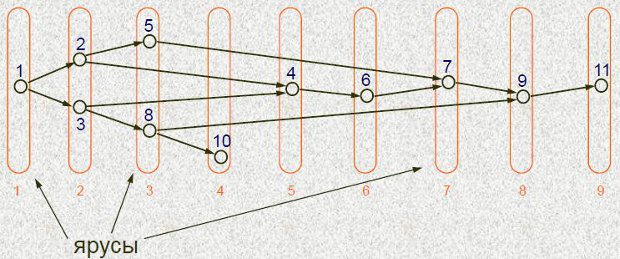
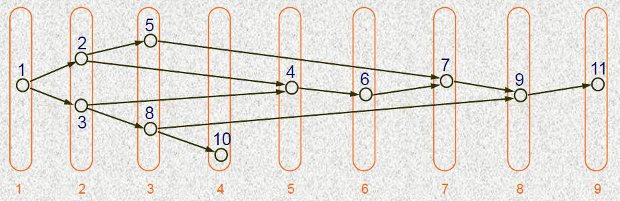
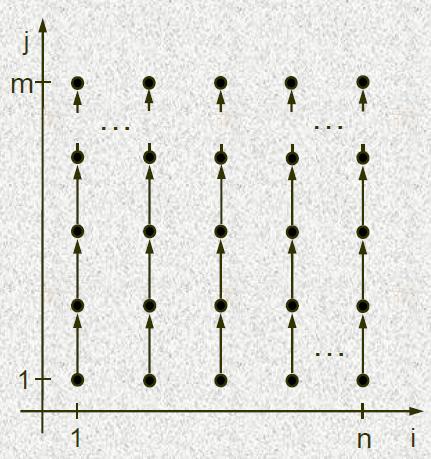
Ярусно-параллельная форма графа алгоритма

Как определить и сделать понятным ресурс параллелизма в графе алгоритма (в программе, в алгоритме) ?

- начальная вершина каждой дуги расположена на ярусе с номером меньшим, чем номер яруса конечной вершины,

- между вершинами, расположенными на одном ярусе, не может быть дуг.

Высота ЯПФ – это число ярусов,

Ширина яруса – число вершин, расположенных на ярусе,

Ширина ЯПФ – это максимальная ширина ярусов в ЯПФ.

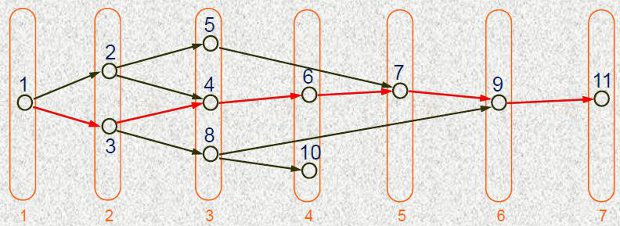
Высота ЯПФ = сложность параллельной реализации алгоритма/программы.

Высота канонической ЯПФ = длине критического пути + 1.

for( i = 0; i < n; ++i)
   for( j = 0; j < m; ++j)
      A[i][j] = A[i][j–1] + C[i][j]∗x;

Чему, согласно закону Амдала, равно максимальное ускорение, которое можно получить при исполнении данного фрагмента на параллельной вычислительной системе?

Закон Амдала:

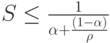
где:

- доля последовательных операций,

– число процессоров в системе.

Виды параллелизма в алгоритмах и программах

Конечный параллелизм определяется информационной независимостью некоторых фрагментов в тексте программы.

Массовый параллелизм определяется информационной независимостью итераций циклов программы.

Конечный параллелизм.

увеличить изображение

Массовый параллелизм.

Координатный параллелизм.

#pragma omp parallel for for( i = 0; i < n; ++i) for( = 0; j < m; ++j) A[i][j] = A[i][j–1] + C[i][j]∗x;

Утверждение: для того чтобы цикл был параллельным необходимо и достаточно, чтобы для любой тройки графа алгоритма данного цикла включение

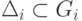
— это многогранник из тройки,

= {f1 = i1,

i1 — это параметр анализируемого цикла,

f1 — это первая компонента векторной функции Fi из тройки.

#pragma omp parallel for for( i = 0; i < n; ++i) for( = 0; j < m; ++j) A[i][j] = A[i][j–1] + C[i][j]∗x;