Операторы языка C#

Задачи

Альтернатива и разбор случаев

• 1. Постройте консольное и Windows-приложение, которое по заданным коэффициентам a, b, c находит корни квадратного уравнения.
• 2. Постройте консольное и Windows-приложение, которое по заданному значению аргумента x вычисляет значение функции y=F(x), где функция F(x) задана соотношением:
  
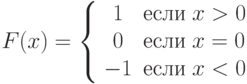
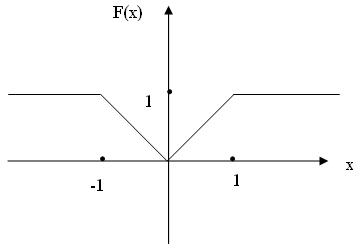
• 3. Постройте консольное и Windows-приложение, которое по заданному значению аргумента x вычисляет значение функции y=F(x), где функция F(x) задана графиком:
  

  
  
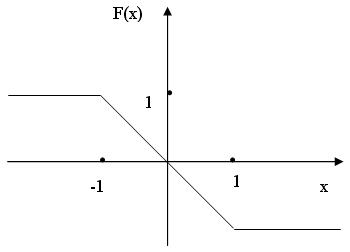
• 4. Постройте консольное и Windows-приложение, которое по заданному значению аргумента x вычисляет значение функции y=F(x), где функция F(x) задана графиком:
  

  
  
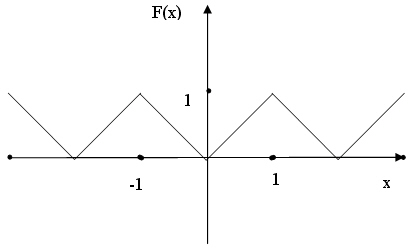
• 5. Постройте консольное и Windows-приложение, которое по заданному значению аргумента x вычисляет значение функции y=F(x), где периодическая функция F(x) задана графиком:
  

  
  
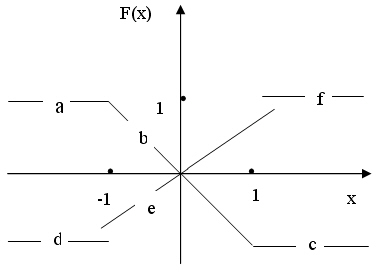
• 6. Постройте консольное и Windows-приложение, которое по заданным координатам x и y определяет, принадлежит ли точка (x, y) одной из 6 дорог (a, b, c, d, e, f), показанных на графике. Если точка принадлежит дороге, то укажите, какой именно дороге, если принадлежит двум дорогам, то и этот факт следует отразить в результирующем сообщении.
  

  
  
• 7. Дана точка A с координатами (x, y) и два прямоугольника Q1 и Q2 со сторонами, параллельными осям координат. Каждый из прямоугольников задается парой точек Q1(p1, p2), Q2(p3, p4), определяющих левый нижний и правый верхний углы прямоугольника. Постройте консольное и Windows-приложение, которое определяет, принадлежит ли точка A(x, y) хотя бы одному из прямоугольников Q1 и Q2. Если точка принадлежит прямоугольнику, то следует сообщить, какому именно прямоугольнику, если принадлежит двум прямоугольникам, то и этот факт должен быть отражен в результирующем сообщении. Если точка принадлежит границе прямоугольника, то и это должно быть отображено в сообщении.
• 8. Дана точка A с координатами (x, y) и мишень - 10 концентрических кругов с центром в начале координат и радиусами R1, R2 … R10. Постройте консольное и Windows-приложение, которое определяет количество выбитых очков. Предполагается, как обычно, что за попадание точки в круг самого малого радиуса начисляется 10 очков и так далее до одного очка. За попадание в "молоко" очки не начисляются.
• 9. Заданы четыре точки на плоскости P1, P2, P3, P4 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Аналогично, точки P3 и P4 задают прямоугольник R2. Определить, пересекаются ли прямоугольники R1 и R2.
• 10. Заданы четыре точки на плоскости P1, P2, P3, P4 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Аналогично, точки P3 и P4 задают прямоугольник R2. Определить, пересекаются ли прямоугольники R1 и R2. Если прямоугольники пересекаются, определить координаты точек P5 и P6, задающих прямоугольник пересечения.
• 11. Заданы четыре точки на плоскости P1, P2, P3, P4 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Аналогично, точки P3 и P4 задают прямоугольник R2. Определить, пересекаются ли прямоугольники R1 и R2. Если прямоугольники пересекаются, определить площадь прямоугольника пересечения.
• 12. Заданы три точки на плоскости P1, P2, P3 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Точка P3 задает центр круга радиуса r. Определить, пересекаются ли прямоугольник R1 и круг.
• 13. Задан круг радиуса r с центром в точке P с координатами x и y. Задана прямая y = b, параллельная оси X. Определить, пересекаются ли круг и прямая.
• 14. Задан круг радиуса r с центром в точке P с координатами x и y. Задана прямая y = b, параллельная оси X. Определить пересекаются ли круг и прямая. Если есть пересечение, то определить координаты точек пересечения.
• 15. Заданы три точки на плоскости P1, P2, P3 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Точка P3 задает центр круга радиуса r. Определить, пересекаются ли прямоугольник R1 и круг. Если есть пересечение, то определить координаты точек пересечения.
• 16. Заданы три точки на плоскости P1, P2, P3 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Точка P3 задает центр круга радиуса r. Определить, пересекаются ли прямоугольник R1 и круг. Если есть пересечение, то определить площадь пересечения.
• 17. Заданы три точки на плоскости P1, P2, P3 своими декартовыми координатами - x и y. Точки P1 и P2 задают левый нижний угол и правый верхний угол прямоугольника R1 со сторонами, параллельными осям координат. Точка P3 задает центр круга радиуса r. Определить число точек с целочисленными координатами внутри области пересечения прямоугольника R1 и круга.
• 18. Заданы четыре точки на плоскости P1, P2, P3, P4 своими декартовыми координатами - x и y. Точки P1 и P2 задают один отрезок прямой, точки P3 и P4 задают другой отрезок прямой. Определить, пересекаются ли отрезки. Если да, то определить координаты точки пересечения.
• 19. (*) Дана точка A с координатами (x, y) и треугольник, заданный своими вершинами - точкам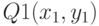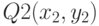и , и 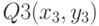. Постройте консольное и Windows-приложение, которое определяет, принадлежит ли точка A треугольнику (находится внутри его или на его границах).
• 20. Дан текст T. Постройте консольное и Windows-приложение, которое проводит частотный анализ, определяя частоту вхождения букв А, Б, … Я (больших и малых) в текст T.
• 21. Дан массив элементов с элементами, принимающими одно из четырех значений: белый, черный, красный, желтый. Постройте консольное и Windows-приложение, которое определяет частоту вхождения элементов каждого цвета в массив.
• 22. Студент, приходящий на экзамен, характеризуется тремя булевскими переменными P1, P2 и P3. Переменная P1 имеет значение true, если студент знает определения, и false в противном случае. Переменная P2 имеет значение true, если студент умеет доказывать теоремы, и false в противном случае. Переменная P3 имеет значение true, если студент умеет решать задачи, и false в противном случае. Постройте консольное и Windows-приложение "Строгий экзаменатор", в котором экзаменатор руководствуется следующим алгоритмом: он спрашивает определение и ставит оценку "неуд" в случае его незнания. Студенту, знающему определение, предлагается доказать теорему, в случае неуспеха ставится оценка "уд". Студенту, знающему определения и умеющему доказывать теоремы, предлагается решить задачу, в случае неуспеха ставится оценка "хор", в случае успеха - "отл".
• 23. Студент, приходящий на экзамен, характеризуется тремя булевскими переменными P1, P2 и P3. Переменная P1 имеет значение true, если студент знает определения, и false в противном случае. Переменная P2 имеет значение true, если студент умеет доказывать теоремы, и false в противном случае. Переменная P3 имеет значение true, если студент умеет решать задачи, и false в противном случае. Постройте консольное и Windows-приложение "Добрый экзаменатор", в котором экзаменатор руководствуется следующим алгоритмом: он предлагает решить задачу и в случае успеха ставит оценку - "отл". Студенту, не умеющему решать задачи, предлагается доказать теорему, в случае успеха ставится оценка "хор". Студенту, не умеющему решать задачи и не умеющему доказывать теоремы, предлагается сформулировать определение и в случае незнания ставится оценка "неуд", в случае успеха ставится оценка "уд".