Теоретические сведения о компьютерных вирусах

Проблема обнаружения вирусов

Вместе с выделением класса вирусов возникает и проблема обнаружения вирусов.

Предполагается, что все данные о структуре программы и машины, на которой она выполняется доступны. Неизвестными являются только данные о вирусе.

Общая проблема обнаружения вирусов

Согласно тезису Тьюринга-Черча, если бы существовал алгоритм обнаружения вирусов, можно было бы создать Машину Тьюринга, которая бы выполняла этот алгоритм. Покажем, что такой Машины Тьюринга не существует.

Доказательство. Согласно теореме 2.7 вместо Машины Тьюринга можно использовать эквивалентную ей RASPM или RASPM с ABS. Рассмотрим программу P, которая эмулирует работу Машины Тьюринга (произвольной). Программа P печатает на выходе 1, если эмулируемая Машина Тьюринга завершает свою работу.

Построим простой вирус, который сперва запускает программу P на случайном, но фиксированном (для данного вируса) входе B, после чего начинает выполнять собственно вирусную часть. При заражении вирус копирует целиком программу P, последовательность B и вирусную часть.

Используя эту конструкцию можно создать программу V в RASPM с ABS для любой Машины Тьюринга, и эта программа будет вирусом в том случае, если она сможет размножаться, т. е. в том случае, когда Машина Тьюринга завершает свою работу на фиксированном для программы V входе или, что тоже самое, если программа P печатает единицу для данной Машины Тьюринга и данного входа.

Предположим, что существует Машина Тьюринга, способная обнаруживать все вирусы, т. е. такая Машина Тьюринга T, которая читает код программы RASPM с ABS и печатает 1, если в коде этой программы содержится вирус, и печатает 0, если вируса нет. Применим машину T к программе V. Если T печатает 1, значит программа P и соответствующая ей Машина Тьюринга завершают свою работу на некотором входе B. Если T печатает 0, значит программа P и соответствующая ей Машина Тьюринга никогда не завершит свою работу на некотором входе B. Учитывая, что вход B и эмулируемая программой P Машина Тьюринга могут быть любыми, получаем, что Машина Тьюринга T способна для любой Машины Тьюринга и любого входа определить, завершит ли данная Машина Тьюринга работу на данном входе. Однако мы знаем, что это невозможно.

Полученное противоречие доказывает теорему.

Оценка сложности сигнатурного метода

Далее в своей работе Ф. Лейтольд обращается к проблеме обнаружения не всех возможных вирусов, а некоторого подмножества "известных" вирусов.

Для этого предлагается сигнатурный метод - обнаружение вируса по строке или подстроке его кода. Естественно, таким образом невозможно обнаружить полиморфные вирусы. Но для обнаружения обычных или олигоморфных вирусов такой способ годится: олигоморфные вирусы могут обнаруживаться по строке или подстроке кода расшифровщика.

В случаях, когда обнаружение осуществляется по подстроке вирусного кода (либо даже по полному коду распаковщика для олигоморфных вирусов) возможны ложные срабатывания. Ф. Лейтольд приводит оценку вероятности ложных обнаружений при следующих допущениях:

• Длина сигнатуры - N
• Общая длина анализируемых данных - L >> N
• Количество символов в алфавите - n, и встречаются они в анализируемых данных с равной вероятностью
• Количество известных вирусов M

В этом случае оценка количества ложных обнаружений будет примерно равна:

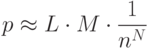
Можно также подсчитать вычислительную сложность алгоритма, выполняющего поиск вирусов по сигнатуре. Для выполнения поиска требуется последовательно сравнить все ячейки анализируемой строки данных с первыми ячейками сигнатур. В общем случае это LxM сравнений. Далее, при обнаружении совпадения потребуется провести сравнение со второй ячейкой сигнатуры. Учитывая вероятность совпадения значения первой ячейки, количество сравнений второй ячейки будет . Аналогично, третьей - 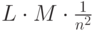и т. д. Общее количество сравнений составит:

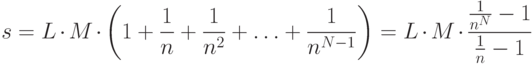
В худшем сценарии, когда все сигнатуры полностью различны, а n и N достаточно велики, количество сравнений составит s = LxMxN.

Следовательно, сигнатурный поиск может быть выполнен за полиномиальное время.

Необходимо понимать, что полученные оценки приблизительны и соответствуют худшему варианту поиска случайной подпоследовательности в случайной последовательности. На практике код программы и код вируса не являются случайными последовательностями и с учетом знания их структуры алгоритм поиска может быть существенно оптимизирован, оценка времени - уменьшена.