| Россия, Республика Хакасия, г. Абакан |
Математическая логика событий и логические нейронные сети
Дерево логических возможностей. Факторное пространство событий
Часто приходится оперировать не отдельными событиями и даже не исчерпывающими множествами таких событий (высказываниями о них), а композициями таких множеств. Между событиями, принадлежащими различным множествам, возможна зависимость, порождающая сложные высказывания. Связи между ИМС, образующие сложные высказывания, отображаются деревом логических возможностей [20].
Рассмотрим пример.
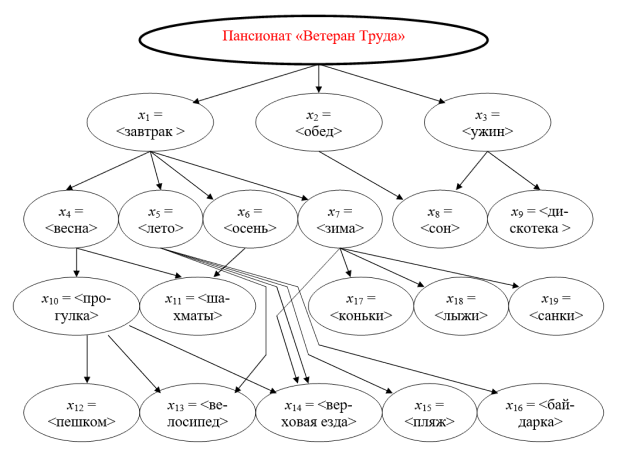
Пансионат для ветеранов труда обеспечивает постояльцам активный отдых круглый год. Представим схемой (рис. 1.1) распорядок дня отдыхающих. Такая схема и определит дерево логических возможностей.
Уровни ветвления могут формироваться разными способами. Например, первый уровень можно сформировать на основе времён года и т.д. Однако в порядке рекомендации можно следовать правилу: события располагаются на более низких уровнях по сравнению с теми уровнями, которые занимают события, от которых зависят данные события.
Бабушка пишет внуку: "Зимой я после завтрака катаюсь на лошади, и летом я после завтрака катаюсь на лошади, а также весной после завтрака прогулка бывает на лошади". …Что-то ей не нравится, и она строит схему своего составного высказывания: 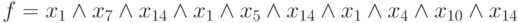 . Несколько поразмыслив, бабушка использует вынесение за скобку:
. Несколько поразмыслив, бабушка использует вынесение за скобку: 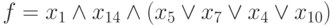 . Тогда окончательный текст сообщения принимает вид: "После завтрака я катаюсь на лошади летом или зимой, а также, бывает, и весной, — вместо прогулки". Как же бабушка определила форму того логического выражения, — функции, отображающей все возможные варианты, и даже пути, ведущие к свершению интересующего события?
. Тогда окончательный текст сообщения принимает вид: "После завтрака я катаюсь на лошади летом или зимой, а также, бывает, и весной, — вместо прогулки". Как же бабушка определила форму того логического выражения, — функции, отображающей все возможные варианты, и даже пути, ведущие к свершению интересующего события?
Ответ следующий: необходимо на каждом пути в дереве логических возможностей, ведущем к заданному событию, построить конъюнкцию событий, образующих этот путь. Затем все такие конъюнкции объединить операцией дизъюнкции. Поскольку используются только исчерпывающие множества событий, очевидно, что эта дизъюнкция выполняется с помощью операции 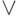 , т.е. ИСКЛЮЧАЮЩЕЕ ИЛИ (хотя можно пользоваться значком
, т.е. ИСКЛЮЧАЮЩЕЕ ИЛИ (хотя можно пользоваться значком 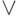 , опираясь на действительный, "физический" смысл возможных событий).
, опираясь на действительный, "физический" смысл возможных событий).
Полученная таким способом функция вызывает естественное желание быть подвергнутой эквивалентному преобразованию — вынесению за скобки. Напомним список эквивалентных преобразований из булевой алгебры (1.3) [4]:
Закон коммутативности: 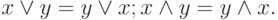
Закон ассоциативности: 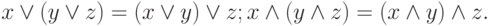
Закон дистрибутивности: 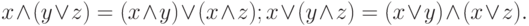
Закон де Моргана:  ;
; 
Закон идемпотенции: 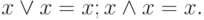
Закон поглощения: 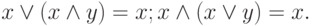
Закон склеивания: 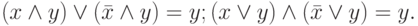
Операция переменной с инверсией: 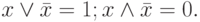
Операция с константами: 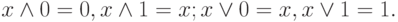
Двойное отрицание: 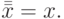
Практически, например, при конструировании электронных устройств, известно заранее, какой сигнал на отдельно взятом выходе должен формироваться при различных значениях сигналов на входе. Тогда значения логической функции, описывающей формирование сигнала на данном выходе, задаются таблично, в зависимости от всех возможных ситуаций на входе. По такой таблице аналитическое выражение для искомой логической функции формируется в виде совершенной дизъюнктивной нормальной формы (СДНФ). Её общий вид продемонстрируем на примере трёх переменных:
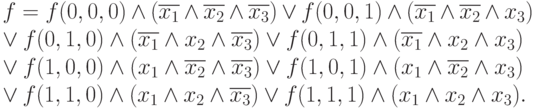
Отметим, что в результате такого способа построения искомая функция принимает вид, при котором каждая используемая переменная-высказывание входит не более одного раза.
Например, функция, отображающая такое событие в жизни бабушки, как езда на велосипеде, имеет вид:

Однако далее будет показано, что не всегда единственного вхождения переменных можно добиться с помощью указанных эквивалентных преобразований. Иногда требуются дополнительные действия для его осуществления.
Определение 1.2. Совокупность всех исследуемых в данном контексте событий, т.е. множество - объединение всех рассматриваемых ИМС, образует факторное пространство событий.
Как и ранее, точку факторного пространства (ситуацию) будем обозначать {x1,..., xn}.
Как видно из примера, факторное пространство событий отображается ветвящейся структурой на основе отдельных исчерпывающих множеств событий, входящих в его состав. Тогда подмножества, состоящие из таких ИМС, тоже являются факторными подпространствами, которые в некотором контексте можно исследовать отдельно.
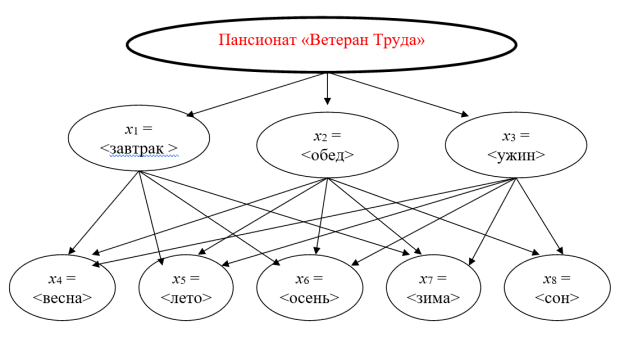
Например, можно отдельно исследовать факторное подпространство, сформированное на основе первых двух уровней ветвления (рис. 1.2) в приведённом на рис. 1.1 дереве логических возможностей. Это может быть необходимо при планировании финансовых расходов пансионата на питание.
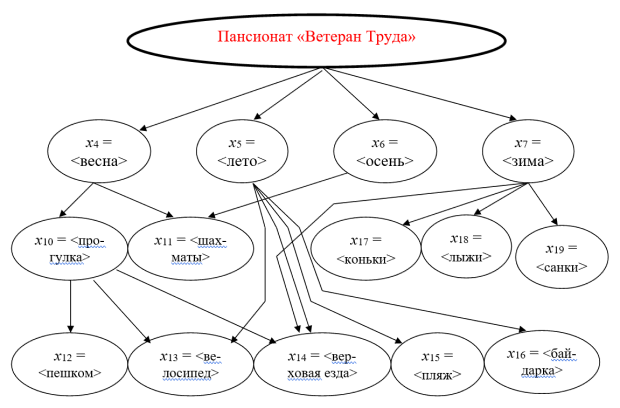
Можно, в соответствии с поставленной задачей (в контексте исследований), формировать другие факторные пространства событий. Например, планирование использования спортивного инвентаря по времени года приводит к целесообразности факторного пространства, структура которого показана на рис. 1.3.
увеличить изображение
Рис. 1.2. Факторное подпространство для исследований финансовых затрат на питание