| Россия |
Обретение навыков построения систем ассоциативных вычислений, распознавания символов и принятия решений
Распознавание нечётких символов персептроном
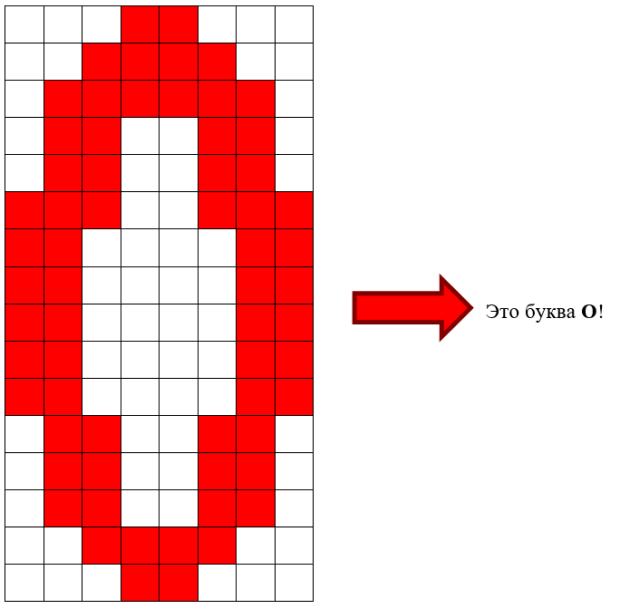
Подобно сетчатке глаза, сформируем экран 8 x 16 клеток. Каждую клетку будем рассматривать в качестве рецептора, способного воспринимать извне величину возбуждения в диапазоне 0 – 1.
Для обучения букве О условно нарисуем на экране эталон этой буквы. Окружим линию этого эталона клетками (рецепторами) с некоторым запасом по толщине линии (как показано на рис. 1.3) так, чтобы создать "ловушку" для захвата основной части нечётко и с искажениями изображаемой буквы О. Соединим все рецепторы "ловушки" буквы О связями (с единичными весами) с нейроном, отвечающим за вывод: "Это буква О".
Выберем функцию активации этого нейрона  при отрицательном значении разности принимающую нулевое значение. Здесь NO – количество рецепторов, образующих "ловушку" буквы О, fi – величина возбуждения i-го рецептора, h – единый порог, подбираемый экспериментально для всех букв, распознаванию которых производится обучение. По рисунку NO = 64.
при отрицательном значении разности принимающую нулевое значение. Здесь NO – количество рецепторов, образующих "ловушку" буквы О, fi – величина возбуждения i-го рецептора, h – единый порог, подбираемый экспериментально для всех букв, распознаванию которых производится обучение. По рисунку NO = 64.
На этом же экране построим "ловушку" для искажённой, "зашумлённой" буквы А, как показано на рис. 8.4. Все рецепторы "ловушки" свяжем с нейроном, отвечающим за вывод: "Это буква А".
Функция активации этого нейрона имеет тот же вид 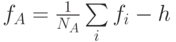 , однако, в нашем примере NA = 74. (Данное нормирование производится для уравнивания значимости всех букв, которым обучается нейросеть.)
, однако, в нашем примере NA = 74. (Данное нормирование производится для уравнивания значимости всех букв, которым обучается нейросеть.)
По чётко заданным эталонам букв (с единичной засветкой клеток экрана по правильному контуру) предварительно подберём порог h так, чтобы существенно возбуждался лишь тот нейрон, который соответствует предъявляемой букве. Показ "чужого" символа, которому нейросеть не обучалась, должен приводить к нулевому возбуждению нейронов. В процессе эксперимента и при добавлении новых букв значение порога может уточняться.
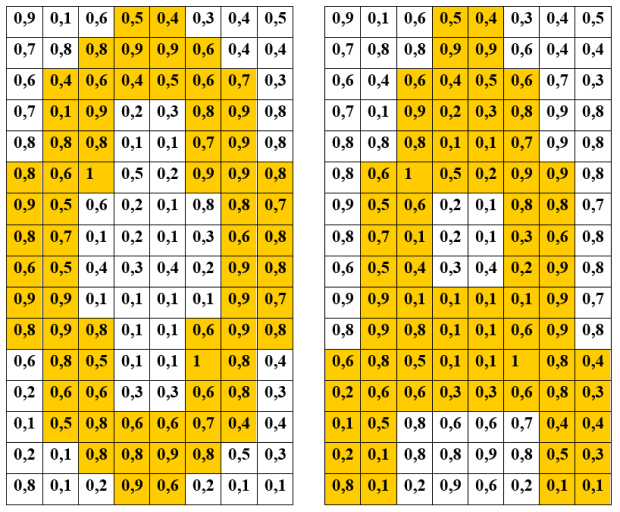
Перейдём к рабочему режиму распознавания. На рис. 8.5 показан вариант зашумлённой засветки экрана. Слева наложена "ловушка" для распознавания буквы О. Справа – "ловушка" для распознавания буквы А.
Сумма сигналов в "ловушке" О равна 49,2. Пусть h = 0,7. Тогда fO = 0,77 - 0,7 = 0,07. Сумма сигналов в "ловушке" А равна 36,9, fA = 0. Нейросеть высказалась за то, что ей была предъявлена "зашумлённая" буква О.
Расширьте эксперимент, произведя обучение для трёх, четырёх и т.д. символов. Выбор набора значительно отличающихся символов определяет вариант выполняемой лабораторной работы. Для представления экрана и для расчётов целесообразно использовать EXEL.
Вы, несомненно, столкнётесь с малой разрешающей способностью экрана 8 x 16. Кроме того, данная лабораторная работа ограничена центровкой и масштабированием образов. Так что перед экспериментатором открываются неограниченные возможности!
Система принятия решений "Железнодорожная рулетка"
Рассмотрим увлекательную детскую игру "Железнодорожная рулетка", основанную на так хорошо знакомой Вам задаче о встрече. Помните: "Из пунктов А и В навстречу друг другу…" и т.д.?
Начальник станции Кукуевка (ведущий) и начальник станции Пырловка одновременно выпускают навстречу друг другу два паровоза (рис. 8.6) со скоростью либо 60, либо 80 км/час. Длина перегона составляет 4 км. Небольшой нюанс заключается в том, что пути перегона то сходятся в один, на протяжении одного километра, то расходятся. И тогда, в зависимости от точки встречи, со станции Кукуевка надо выслать на соответствующий километр либо линейного - даму с приветственным платочком, либо линейного с подстилочной соломкой.
Решение о такой посылке усложняется помехами в линии передачи данных, в связи с чем скорости паровозов сообщаются с достоверностью, меньшей единицы. Кроме того, необходимо каждый эксперимент связать с ожидаемыми денежными затратами на единовременную добавку к пенсии линейных.
Тогда Вы понимаете, что без элементов искусственного интеллекта не обойтись. Вы ищете что-то похожее на табличный метод, но с автоматической интерполяцией, что-то связанное с ассоциативным мышлением… И Вы решаетесь…
Произведём предварительные расчёты, чтобы представить себе все варианты будущего поведения нашей системы принятия решений — для её обучения. Представим (рис. 8.7) графически структуру логического функционирования создаваемой системы принятия решений для каждой возможной ситуации.
Ситуация 1. Кукуевский паровоз имеет скорость 60 км/ч (Событие А1). Пырловский паровоз имеет скорость 60 км/ч (Событие В1). Одновременное выполнение этих событий обозначим А1&В1. Тогда точка встречи находится как раз посредине перегона, что, скорее всего, требует помощи линейного с соломкой. Но возможно и везение за счёт неточного определения скоростей. Тогда на всякий случай потребуется дама с платочком. Принимаемое решение, заключающееся в отправлении обоих линейных на границу второго и третьего километров, назовём решением R1. С ним связаны расходы на единовременное пособие М1.
Ситуация 2. Кукуевский паровоз имеет скорость 60 км/ч (Событие А1), но пырловский паровоз имеет скорость 80 км/ч (Событие В2). (Выполняется условие А1&В2.) Тогда их точка встречи находится на втором километре пути, и, следовательно, требует решения R2: "Отправить даму с платочком на второй километр!" В активе указанной дамы появляется сумма М2 условных единиц.
Ситуация 3. Кукуевский паровоз имеет скорость 80 км/ч (Событие А2), пырловский паровоз имеет скорость 60 км/ч (Событие В1). (Выполняется условие А2&В1.) Тогда их точка встречи находится на третьем километре пути, что требует сочувственного вмешательства линейного с соломкой (решение R3), с оплатой труда в М3 условных единиц.
Ситуация 4. Кукуевский и пырловский паровозы имеют скорость 80 км/ч (Событие А2&В2), что, ввиду высокой скорости перемещения линейных в середину перегона, требует решения R4 с затратами М4.
А теперь оживим эту структуру, заставим её действовать, как, по-видимому, на логическом уровне действуют структуры нашего мозга.
Представим себе, что на месте каждого овала (потом — кружочка, на рисунке 8.7 справа) действует нейроподобный элемент (просто нейрон). Нейроны входного слоя — рецепторы приходят в возбуждённое состояние извне (подобно сетчатке глаза) в соответствии с той ситуацией, которую мы задаём на входе системы. Например, мы хотим испытать ситуацию А1&В2. Тогда мы полагаем величины возбуждения рецепторов А1 и В2 равными единице и записываем: VA1 = VB2 = 1. При этом мы не забываем позаботиться о том, чтобы величины возбуждений нейронов А2 и В1 остались равными нулю.
Для нейронов, "принимающих" возбуждение рецепторов в соответствии со стрелками, введём функцию активации, в результате выполнения которой формируется величина V возбуждения каждого нейрона. Для нашего случая, не долго думая (ибо существует большой произвол в выборе вида функции активации, на любой вкус), определим вид такой функции

где i — индекс нейрона (в данном случае – рецептора), "передающего" своё возбуждение данному нейрону, h — порог.
Положим h = 1 и рассчитаем величины возбуждения нейронов R1 ( R4 для чётко заданной единицами, эталонной, ситуации А1& В2
VR1: 1 + 0 - 1 = 0, VR1 = 0; VR2: 1 + 1 - 1 = 1, VR2 = 1; VR3: 0 + 0 - 1 = -1, VR3 = 0; VR4: 0 + 1 - 1 = 0, VR4 = 0.
Таким образом, "высветилось" то решение, которое необходимо принять, и старт линейным должен быть дан. Продолжим верификацию проверкой, что так же работает наша сеть по всем эталонам, по которым мы её обучили, проложив "проводочки" от каждой исходной посылки к следствию.
Теперь поэкспериментируем.
Задавая события по принципу "да - нет", "1 - 0", мы предполагали булевский тип исходных данных. А что, если поменять, обобщить тип исходных данных, допустив рассмотрение нечётких значений возбуждения рецепторов, интерпретируемых как достоверность? Или даже каких-то других взаимных оценок, которые используются часто в быту людьми, не сведущими в теории вероятности и не знакомых с понятием "исчерпывающее множество событий"?
Например, в результате искажения информации начальник станции Кукуевка принял решение считать скорость пырловского паровоза равной не то 60, не то 80 км/ч. Но, скорее всего — 60! И подойдя к компьютеру, он по наитию набирает: А1 = 1, А2 = 0, В1 = 0,7, В2 = 0,4. На какую ситуацию это указывает, и какое решение наиболее правильно? Считаем:
VR1: 1 + 0,7 - 1 = 0,7, VR1 = 0,7; VR2: 1 + 0,4 - 1 = 0,4, VR2 = 0,4; VR3: 0 + 0,7 - 1 = -0,3, VR3 = 0; VR4: 0 + 0,4 - 1 = -0,6, VR4 = 0.
Мы видим, что максимальной величины возбуждения достиг нейрон R1, определивший главное решение. Но мы вправе учесть и решение R2 с меньшим приоритетом, дав даме с платочком дополнительные указания. И в этом проявится наша мудрость.
По известной формуле нахождения среднего мы можем оценить математическое ожидание того, на сколько облегчится карман начальника Кукуевской станции:

где М1 – М4 – конечно же неизвестные нам (и налоговому инспектору) суммы.