|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистический анализ числовых величин (непараметрическая статистика)
Неустойчивость параметрических методов отбраковки резко выделяющихся результатов наблюдений
При обработки реальных экономических данных, полученных в процессе наблюдений, измерений, расчетов, иногда один или несколько результатов наблюдений резко выделяются, т.е. далеко отстоят от основной массы данных. Такие резко выделяющиеся результаты наблюдений часто считают содержащими грубые погрешности, соответственно называют промахами или выбросами. В рассматриваемых случаях возникает естественная мысль о том, что подобные наблюдения не относятся к изучаемой совокупности, поскольку содержат грубую погрешность, а получены в результате ошибки, промаха. В метрологии об этом явлении говорят так: "Грубые погрешности и промахи возникают из-за ошибок или неправильных действий оператора (его психо-физиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов и т.п.), а также при кратковременных резких изменений проведения измерений (вибрации, поступления холодного воздуха, толчка прибора оператором и т.п.). Если грубые погрешности и промахи обнаруживают в процессе измерений, то результаты, содержащие их, отбрасывают. Однако чаще всего их выявляют только при окончательной обработке результатов измерений с помощью специальных критериев оценки грубых погрешностей" [7, с.46-47].
Есть два подхода к обработке данных, которые могут быть искажены грубыми погрешностями и промахами:
- отбраковка резко выделяющихся результатов наблюдений, т.е. обнаружение наблюдений, искаженных грубыми погрешностями и промахами, и исключение их из дальнейшей статистической обработки;
- применение устойчивых (робастных) методов обработки данных, На результаты работы которых мало влияет наличие небольшого числа грубо искаженных наблюдений
В настоящем пункте обсуждаются методы отбраковки.
Наиболее изучена ситуация, когда результаты наблюдений - числа  ., резко выделяется один результат наблюдения, для определенности, максимальный xmax .
., резко выделяется один результат наблюдения, для определенности, максимальный xmax .
Простейшая вероятностно-статистическая модель такова [8]. При нулевой гипотезе  результаты наблюдения
результаты наблюдения  рассматриваются как реализация независимых одинаково распределенных случайных величин числа
рассматриваются как реализация независимых одинаково распределенных случайных величин числа  . с функцией распределения
. с функцией распределения  . При альтернативной гипотезе
. При альтернативной гипотезе  случайные величины
случайные величины 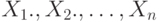 . также независимы,
. также независимы, 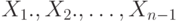 имеют распределение
имеют распределение  , а
, а 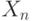 - распределение
- распределение 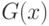 , оно "существенно сдвинуто вправо" относительно
, оно "существенно сдвинуто вправо" относительно  , например,
, например, 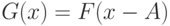 , где
, где  достаточно велико. Если альтернативная гипотеза справедлива, то при
достаточно велико. Если альтернативная гипотеза справедлива, то при 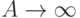 вероятность равенства
вероятность равенства
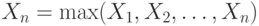
стремится к 1, поэтому естественно применять решающее правило следующего вида:
если  , то принять
, то принять  ,
,
если 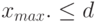 , то принять
, то принять 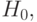 (1)
(1)
где  - параметр решающего правила, который следует определять из вероятностно-статистических соображений.
- параметр решающего правила, который следует определять из вероятностно-статистических соображений.
При справедливости нулевой гипотезы
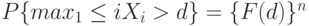
Статистический критерий проверки гипотезы 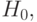 основанный на решающем правиле вида (1), имеет уровень значимости
основанный на решающем правиле вида (1), имеет уровень значимости  , если
, если
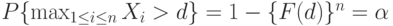
т.е.
![F(d)=\sqrt[n]{1-\alpha}](/sites/default/files/tex_cache/6dc8a38bcbe24530f161178b858eb6f6.png) |
( 2) |
Из соотношения (2) определяют граничное значение 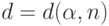 в решающем правиле (1).
в решающем правиле (1).
При больших  и малых
и малых 
![F(d)=\sqrt[n]{1- \alpha}=1-\frac{\alpha}{n}+O \left( \frac{\alpha^2}{n^2} \right)](/sites/default/files/tex_cache/26a0d3c5daecd4b3172e8fbe2a9b6fac.png) |
( 3) |
поэтому в качестве хорошего приближения к 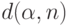 рассматривают
рассматривают  - квантиль распределения
- квантиль распределения  .
.
Пусть правило отбраковки задано в соответствии с выражениями (1) и (2) с некоторой функцией распределения  , однако выборка берется из функции распределения
, однако выборка берется из функции распределения  , мало отличающейся от
, мало отличающейся от  в смысле расстояния Колмогорова
в смысле расстояния Колмогорова
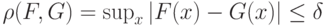 |
( 4) |
С помощью соотношения (3) получаем, что величина 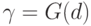 для
для  из уравнения (2) находится между
из уравнения (2) находится между 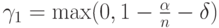 и
и  . Уровень значимости критерия, построенного для
. Уровень значимости критерия, построенного для  , при применении к наблюдениям из
, при применении к наблюдениям из  есть
есть 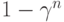 и может принимать любые значения в отрезке
и может принимать любые значения в отрезке ![[1- \gamma_2^n; 1-\gamma_1^n]](/sites/default/files/tex_cache/f75ddced173f70bbcbbb9e1dc2c0ebe5.png) . В частности, при
. В частности, при  возможные значения уровня значимости заполняют отрезок [0; 0,1], т.е. уровень значимости может быть в 2 раза выше номинального, а если n возрастает до 30, то максимальный уровень значимости есть 0,297, т.е. почти в 6 раз выше номинального. При дальнейшем росте n верхняя граница для уровня значимости, как нетрудно видеть, приближается к 1.
возможные значения уровня значимости заполняют отрезок [0; 0,1], т.е. уровень значимости может быть в 2 раза выше номинального, а если n возрастает до 30, то максимальный уровень значимости есть 0,297, т.е. почти в 6 раз выше номинального. При дальнейшем росте n верхняя граница для уровня значимости, как нетрудно видеть, приближается к 1.
Рассмотрим и другой вопрос - насколько правило отбраковки с уровнем значимости  для
для  может отличаться от такового для
может отличаться от такового для  при справедливости неравенства (4). С использованием соотношения (3) заключаем, что из
при справедливости неравенства (4). С использованием соотношения (3) заключаем, что из
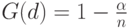 |
( 5) |
следует, что 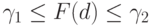 где
где 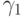 и
и 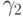 выписаны выше. Решение уравнения (5) может принимать любое значение в отрезке
выписаны выше. Решение уравнения (5) может принимать любое значение в отрезке ![[F^{-1}(\gamma_1); F^{-1}(\gamma_2)]](/sites/default/files/tex_cache/de0a90b8a30e356e0e7fb96913c3ab3d.png) . В частности, при
. В частности, при 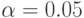 и
и 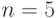 для стандартного нормального распределения F имеем
для стандартного нормального распределения F имеем  , при
, при 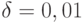 решение уравнения (5) может принимать любое значение в отрезке
решение уравнения (5) может принимать любое значение в отрезке ![[2,054; + \infty]](/sites/default/files/tex_cache/442fe50d1ac637c801c5ca3ec20b2a6c.png) , при
, при 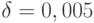 - любое значение в [2,170; 2,576].
- любое значение в [2,170; 2,576].
При использовании любого другого расстояния между функциями распределения выводы о неустойчивости правил отбраковки также справедливы. Отметим, что проведенные рассмотрения выполнены в рамках "общей схемы устойчивости" (см. ниже лекцию об устойчивости статистических процедур).
Рассмотренные примеры показывают, что при конкретном значении 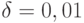 в неравенстве (4) весьма неустойчивы как уровни значимости при фиксированном правиле отбраковки, так и параметр
в неравенстве (4) весьма неустойчивы как уровни значимости при фиксированном правиле отбраковки, так и параметр  правила отбраковки при фиксированном уровне значимости. Обсудим, насколько реалистично определение функции распределения с точностью
правила отбраковки при фиксированном уровне значимости. Обсудим, насколько реалистично определение функции распределения с точностью 
Есть два подхода к определению функции распределения результатов наблюдений: эвристический подбор с последующей проверкой с помощью критериев согласия и вывод из некоторой вероятностной модели.
Пусть с помощью критерия согласия Колмогорова проверяется гипотеза о том, что выборка взята из распределения  . Пусть функции распределения
. Пусть функции распределения  и
и  удовлетворяют соотношению (4). Пусть на самом деле выборка взята из распределения
удовлетворяют соотношению (4). Пусть на самом деле выборка взята из распределения  , а не
, а не  . При каких
. При каких  не удастся различить
не удастся различить  и
и  ? Для определенности, при каких
? Для определенности, при каких  гипотеза согласия с
гипотеза согласия с  будет приниматься не менее чем в 50% случаев?
будет приниматься не менее чем в 50% случаев?
Критерий согласия Колмогорова основан на статистике
 |
( 6) |
где расстояние  между функциями распределения определено выше в формуле (4);
между функциями распределения определено выше в формуле (4);  - та функция распределения, согласие с которой проверяется, а
- та функция распределения, согласие с которой проверяется, а 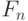 - эмпирическая функция распределения (т.е.
- эмпирическая функция распределения (т.е. 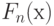 равно доле наблюдений, меньших
равно доле наблюдений, меньших  , в выборке объема
, в выборке объема  ). Как показал А.Н. Колмогоров в 1933 г., функция распределения случайной величины
). Как показал А.Н. Колмогоров в 1933 г., функция распределения случайной величины  при росте объема выборки
при росте объема выборки  сходится к некоторой функции распределения
сходится к некоторой функции распределения 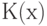 , которую ныне называют функцией Колмогорова. При этом
, которую ныне называют функцией Колмогорова. При этом  и
и 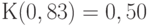 .
.
Поскольку выборка взята из распределения  , то с вероятностью 0,50
, то с вероятностью 0,50
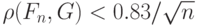 |
( 7) |
(при больших  ). Тогда для рассматриваемой выборки с учетом неравенства (4) и неравенства треугольника для расстояния Колмогорова и симметричности этого расстояния имеем
). Тогда для рассматриваемой выборки с учетом неравенства (4) и неравенства треугольника для расстояния Колмогорова и симметричности этого расстояния имеем
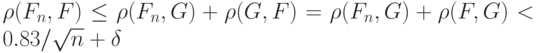
Если
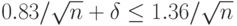
т.е.
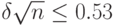 |
( 8) |
то, согласно формуле (6), гипотеза согласия принимается по крайней мере с той же вероятностью, с которой выполнено неравенств (7), т.е. с вероятностью не менее 0,50. Для 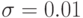 это условие выполняется при
это условие выполняется при 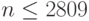 . Таким образом, для определения функции распределения с точностью
. Таким образом, для определения функции распределения с точностью 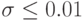 с помощью критерия согласия Колмогорова необходимо несколько тысяч наблюдений, что для большинства эконометрических задач нереально.
с помощью критерия согласия Колмогорова необходимо несколько тысяч наблюдений, что для большинства эконометрических задач нереально.
При втором из названных выше подходов к определению функции распределения ее конкретный вид выводится из некоторой системы аксиом, в частности, из некоторой модели порождения соответствующей случайной величины. Например, из модели суммирования вытекает нормальное распределение, а из мультипликативной модели перемножения - логарифмически нормальное распределение. Как правило, при выводе используется предельный переход. Так, из Центральной Предельной Теоремы теории вероятностей вытекает, что сумма независимых случайных величин может быть приближена нормальным распределением. Однако более детальный анализ, в частности, с помощью неравенства Берри-Эссеена (см. предыдущий пункт) показывает, что для гарантированного достижения точности 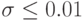 необходимо более полутора тысяч слагаемых. Такого количества слагаемых реально, конечно, указать почти никогда нельзя. Это означает, что при решении практических эконометрических задач теория дает возможность лишь сформулировать гипотезу о виде функции распределения, а проверять ее надо с помощью анализа реальной выборки объема, как показано выше, не менее нескольких тысяч.
необходимо более полутора тысяч слагаемых. Такого количества слагаемых реально, конечно, указать почти никогда нельзя. Это означает, что при решении практических эконометрических задач теория дает возможность лишь сформулировать гипотезу о виде функции распределения, а проверять ее надо с помощью анализа реальной выборки объема, как показано выше, не менее нескольких тысяч.
Таким образом, в большинстве реальных ситуаций определить функцию распределения с точностью 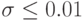 невозможно.
невозможно.
Итак, показано, что правила отбраковки, основанные на использовании конкретной функции распределения, являются крайне неустойчивыми к отклонениям от нее распределения элементов выборки, а гарантировать отсутствие подобных отклонений невозможно. Поэтому отбраковка по классическим правилам математической статистики не является научно обоснованной, особенно при больших объемах выборок. Указанные правила целесообразно применять лишь для выявления "подозрительных" наблюдений, вопрос об отброаковке которых должен решаться из соображений соответствующей предметной области, а не из формально-математических соображений.
Выше для простоты изложения рассмотрен лишь случай полностью известного распределения F, для которого изучено правило отбраковки, заданное формулами (1) и (2). Аналогичные выводы о крайней неустойчивости правил отбраковки справедливы, если "истинное распределение" принадлежит какому-либо параметрическому семейству, например, нормальному, Вейбулла-Гнеденко, гамма.
Параметрическим методам отбраковки, основанным на моделях тех или иных параметрических семейств распределений, посвящены тысячи книг и статей. Приходится признать, что они имеют в основном внутриматематический интерес. При обработке реальных данных следует применять устойчивые методы, в частности, непараметрические.
