|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Нечеткие и случайные множества
П2-4. Пересечения и произведения нечетких и случайных множеств
Выясним, как операции над случайными множествами соотносятся с операциями над их проекциями. В силу законов де Моргана (теорема 1) и теоремы 5 достаточно рассмотреть операцию пересечения случайных множеств.
Теорема 6. Если случайные подмножества 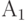 и
и 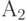 конечного множества
конечного множества 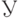 независимы, то нечеткое множество
независимы, то нечеткое множество  является произведением нечетких множеств
является произведением нечетких множеств  и
и  .
.
Доказательство. Надо показать, что для любого 
 |
( 8) |
По формуле для вероятности накрытия точки случайным множеством ( "Статистика нечисловых данных" )
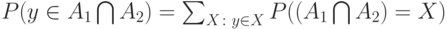 |
( 9) |
Как известно, распределение пересечения случайных множеств  можно выразить через их совместное распределение следующим образом:
можно выразить через их совместное распределение следующим образом:
 |
( 10) |
Из соотношений (9) и (10) следует, что вероятность накрытия для пересечения случайных множеств можно представить в виде двойной суммы
 |
( 11) |
Заметим теперь, что правую часть формулы (11) можно переписать следующим образом:
 |
( 12) |
Действительно, формула (11) отличается от формулы (12) лишь тем, что в ней сгруппированы члены, в которых пересечение переменных суммирования  принимает постоянное значение. Воспользовавшись определением независимости случайных множеств и правилом перемножения сумм, получаем, что из (11) и (12) вытекает равенство
принимает постоянное значение. Воспользовавшись определением независимости случайных множеств и правилом перемножения сумм, получаем, что из (11) и (12) вытекает равенство
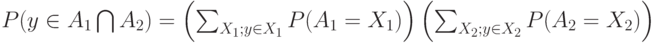
Для завершения доказательства теоремы 6 достаточно еще раз сослаться на формулу для вероятности накрытия точки случайным множеством ( "Статистика нечисловых данных" ).
Определение 3. Носителем случайного множества  называется совокупность всех тех элементов
называется совокупность всех тех элементов  для которых
для которых 
Теорема 7. Равенство

верно тогда и только тогда, когда пересечение носителей случайных множеств  и
и  пусто.
пусто.
Доказательство. Необходимо выяснить условия, при которых
 |
( 13) |
Положим

Тогда равенство (13) сводится к условию
 |
( 14) |
Ясно, что соотношение (14) выполнено тогда и только тогда, когда  при всех
при всех  т.е. не существует ни одного элемента
т.е. не существует ни одного элемента 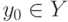 такого, что одновременно
такого, что одновременно  и
и  , а это эквивалентно пустоте пересечения носителей случайных множеств
, а это эквивалентно пустоте пересечения носителей случайных множеств  и
и  . Теорема 7 доказана.
. Теорема 7 доказана.
П2-5. Сведение последовательности операций над нечеткими множествами к последовательности операций над случайными множествами
Выше получены некоторые связи между нечеткими и случайными множествами. Стоит отметить, что изучение этих связей в работе [5] (эта работа выполнена в 1974 г. и доложена на семинаре "Многомерный статистический анализ и вероятностное моделирование реальных процессов" 18 декабря 1974 г. - см. [5, с.169]) началось с введения случайных множеств с целью развития и обобщения аппарата нечетких множеств Л. Заде. Дело в том, что математический аппарат нечетких множеств не позволяет в должной мере учитывать различные варианты зависимости между понятиями (объектами), моделируемыми с его помощью, не является достаточно гибким. Так, для описания "общей части" двух нечетких множеств есть лишь две операции - произведение и пересечение. Если применяется первая из них, то фактически предполагается, что множества ведут себя как проекции независимых случайных множеств (см. выше теорему 6). Операция пересечения также накладыва ет вполне определенные ограничения на вид зависимости между множествами (см. выше теорему 7), причем в этом случае найдены даже необходимые и достаточные условия. Желательно иметь более широкие возможности для моделирования зависимости между множествами (понятиями, объектами). Использование математического аппарата случайных множеств предоставляет такие возможности.
Цель сведения нечетких множеств к случайным состоит в том, чтобы за любой конструкцией из нечетких множеств видеть конструкцию из случайных множеств, определяющую свойства первой, аналогично тому, как плотностью распределения вероятностей мы видим случайную величину. В настоящем пункте приводим результаты по сведению алгебры нечетких множеств к алгебре случайных множеств.
Определение 4. Вероятностное пространство 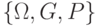 назовем делимым, если для любого измеримого множества
назовем делимым, если для любого измеримого множества  и любого положительного числа
и любого положительного числа  , меньшего
, меньшего  , можно указать измеримое множество
, можно указать измеримое множество 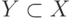 такое, что
такое, что 
Пример. Пусть  - единичный куб конечномерного линейного пространства,
- единичный куб конечномерного линейного пространства,  есть сигма-алгебра борелевских множеств, а
есть сигма-алгебра борелевских множеств, а  - мера Лебега. Тогда
- мера Лебега. Тогда 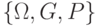 - делимое вероятностное пространство.
- делимое вероятностное пространство.
Таким образом, делимое вероятностное пространство - это не экзотика. Обычный куб является примером такого пространства.
Доказательство сформулированного в примере утверждения проводится стандартными математическими приемами, основанными на том, что измеримое множество можно сколь угодно точно приблизить открытыми множествами, последние представляются в виде суммы не более чем счетного числа открытых шаров, а для шаров делимость проверяется непосредственно (от шара  тело объема
тело объема 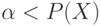 отделяется соответствующей плоскостью).
отделяется соответствующей плоскостью).
Теорема 8. Пусть даны случайное множество  на делимом вероятностном пространстве
на делимом вероятностном пространстве 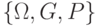 со значениями во множестве всех подмножеств множества
со значениями во множестве всех подмножеств множества 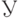 из конечного числа элементов, и нечеткое множество
из конечного числа элементов, и нечеткое множество  на
на 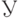 . Тогда существуют случайные множества
. Тогда существуют случайные множества  на том же вероятностном пространстве такие, что
на том же вероятностном пространстве такие, что

где  .
.
Доказательство. В силу справедливости законов де Моргана для нечетких (см. теорему 1 выше) и для случайных множеств, а также теоремы 5 выше (об отрицаниях) достаточно доказать существование случайных множеств  и
и 
Рассмотрим распределение вероятностей во множестве всех подмножеств множества 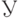 , соответствующее случайному множеству
, соответствующее случайному множеству  такому, что
такому, что  (оно существует в силу теоремы 3). Построим случайное множество
(оно существует в силу теоремы 3). Построим случайное множество  с указанным распределением, независимое от
с указанным распределением, независимое от  . Тогда
. Тогда  по теореме 6.
по теореме 6.
Перейдем к построению случайного множества  . По теореме 7 необходимо и достаточно определить случайное множество
. По теореме 7 необходимо и достаточно определить случайное множество  так, чтобы
так, чтобы  и пересечение носителей случайных множеств
и пересечение носителей случайных множеств  и
и  было пусто, т.е.
было пусто, т.е.  для
для 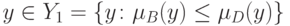 и
и  для
для  .
.
Построим  , исходя из заданного случайного множества
, исходя из заданного случайного множества  Пусть
Пусть  . Исключим элемент
. Исключим элемент 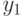 из
из  для стольких элементарных событий
для стольких элементарных событий  , чтобы для полученного случайного множества
, чтобы для полученного случайного множества  было справедливо равенство
было справедливо равенство

(именно здесь используется делимость вероятностного пространства, на котором задано случайное множество  ). Для
). Для  , очевидно,
, очевидно,

Аналогичным образом последовательно исключаем  из
из  для всех
для всех  и добавляем у в
и добавляем у в  для всех
для всех  , меняя на каждом шагу
, меняя на каждом шагу  только для
только для  так, чтобы
так, чтобы

(ясно, что при рассмотрении  случайное множество
случайное множество  не меняется). Перебрав все элементы
не меняется). Перебрав все элементы 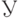 , получим случайное множество
, получим случайное множество  , для которого выполнено требуемое. Теорема 8 доказана.
, для которого выполнено требуемое. Теорема 8 доказана.
Основной результат о сведении теории нечетких множеств к теории случайных множеств дается следующей теоремой.
Теорема 9. Пусть  - некоторые нечеткие подмножества множества
- некоторые нечеткие подмножества множества 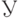 из конечного числа элементов. Рассмотрим результаты последовательного выполнения теоретико-множественных операций
из конечного числа элементов. Рассмотрим результаты последовательного выполнения теоретико-множественных операций

где - символ одной из следующих теоретико-множественных операций над нечеткими множествами: пересечение, произведение, объединение, сумма (на разных местах могут стоять разные символы). Тогда существуют случайные подмножества  того же множества
того же множества 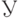 такие, что
такие, что

и, кроме того, результаты теоретико-множественных операций связаны аналогичными соотношениями

где знак  означает, что на рассматриваемом месте стоит символ пересечения
означает, что на рассматриваемом месте стоит символ пересечения  случайных множеств, если в определении
случайных множеств, если в определении 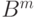 стоит символ пересечения или символ произведения нечетких множеств, и соответственно символ объединения
стоит символ пересечения или символ произведения нечетких множеств, и соответственно символ объединения  случайных множеств, если в
случайных множеств, если в 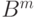 стоит символ объединения или символ суммы нечетких множеств.
стоит символ объединения или символ суммы нечетких множеств.
Комментарий. Поясним содержание теоремы. Например, если

то

Как совместить справедливость дистрибутивного закона для случайных множеств (вытекающего из его справедливости для обычных множеств) с теоремой 2 выше, в которой показано, что для нечетких множеств, вообще говоря,  ? Дело в том, что хотя в соответствии с теоремой 9 для любых трех нечетких множеств
? Дело в том, что хотя в соответствии с теоремой 9 для любых трех нечетких множеств 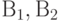 и
и  можно указать три случайных множества
можно указать три случайных множества  и
и 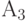 такие, что
такие, что

где

но при этом, вообще говоря,

и, кроме случаев, указанных в теореме 2,

Доказательство теоремы 9 проводится по индукции. При t=1 распределение случайного множества строится с помощью теоремы 3. Затем конструируется само случайное множество 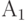 , определенное на делимом вероятностном пространстве (нетрудно проверить, что на делимом вероятностном пространстве можно построить случайное подмножество конечного множества с любым заданным распределением именно в силу делимости пространства). Далее случайные множества
, определенное на делимом вероятностном пространстве (нетрудно проверить, что на делимом вероятностном пространстве можно построить случайное подмножество конечного множества с любым заданным распределением именно в силу делимости пространства). Далее случайные множества  строим по индукции с помощью теоремы 8. Теорема 9 доказана.
строим по индукции с помощью теоремы 8. Теорема 9 доказана.
Замечание. Проведенное доказательство теоремы 9 проходит и в случае, когда при определении 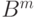 используются отрицания, точнее, кроме
используются отрицания, точнее, кроме 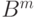 ранее введенного вида используются также последовательности результатов теоретико-множественных операций, очередной шаг в которых имеет вид
ранее введенного вида используются также последовательности результатов теоретико-множественных операций, очередной шаг в которых имеет вид

А именно, сначала при помощи законов де Моргана (теорема 1 выше) проводится преобразование, в результате которого в последовательности 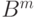 остаются только отрицания отдельных подмножеств из совокупности
остаются только отрицания отдельных подмножеств из совокупности  , а затем с помощью теоремы 5 вообще удается избавиться от отрицаний и вернуться к условиям теоремы 9.
, а затем с помощью теоремы 5 вообще удается избавиться от отрицаний и вернуться к условиям теоремы 9.
Итак, в настоящем приложении описаны связи между такими объектами нечисловой природы, как нечеткие и случайные множества, установленные в нашей стране в первой половине 1970-х годов. Через несколько лет, а именно, в начале 1980-х годов, близкие подходы стали развиваться и за рубежом. Одна из работ [6] носит примечательное название "Нечеткие множества как классы эквивалентности случайных множеств".
В эконометрике разработан ряд методов статистического анализа нечетких данных, в том числе методы классификации, регрессии, проверки гипотез о совпадении функций принадлежности по опытным данным и т.д., при этом оказались полезными общие подходы статистики объектов нечисловой природы (см. "Статистика нечисловых данных" и работы [1],[2],[5]). Методологические и прикладные вопросы теории нечеткости мы обсуждали в работах [1], [2], [7].

