| Россия |
Пространство отображения (моделирования) систем
4.4. Подпространства состояний.
Подпространства состояний Si отражают соответствующие свойства si систем и имеют базис в виде <sij, sijk>. Более точно топология задается законами свойства si или соответствующими частно-научными теориями. В частном случае подпространство Si может быть какого-либо известного в математике типа: топологического, нормированного, метрического, линейного, арифметического, евклидова, векторного, гильбертова и т. д. [101]. Определение отдельных из этих пространств мы уже ранее приводили и использовали (см. §§2.3, 4.1, 4.2).
* ЧАСТНЫЙ СЛУЧАЙ I [35].
Функционирование технической системы может характеризоваться целью минимизации целевой функции и описываться системой уравнений. Установление связи между ними заключается в составлении уравнений Эйлера-Лежандра или получением из цели преобразованием Лежандра функции Гамильтона и составлением канонических уравнений — Гамильтоновой системы. При этом возникает задача составления базиса свойств, выделение тех свойств, которые вносят существенный вклад в цель, и свойств, фактически не влияющих на цель. Это задача содержательной модели системы.
* ПРИМЕРЫ [114].
1) В классической механике элементарными объектами являются материальные точки вместе с их положениями и скоростями в физическом пространстве, а изменчивость задается траекториями точек. Пространство состояний есть шестимерное фазовое пространство — произведение трехмерного евклидова пространства на трехмерное пространство скоростей.
2) В квантовой механике элементарные объекты — амплитуды вероятностей состояний микрообъектов (например, энергетических состояний атома). Изменчивость в пространстве состояний задается траекториями векторов в бесконечномерном гильбертовом пространстве.
3) В теории ядра элементарные объекты — нуклоны и некоторые другие элементарные частицы, обладающие специфическим набором квантовых чисел. Изменчивость — взаимные превращения частиц и излучений. Пространство состояний ограничивается комбинациями квантовых чисел для совокупностей превращающихся частиц, допустимыми согласно законам сохранения.
4) В эмбриологии роль элементарного объекта играет живая клетка, а роль изменчивости — процесс деления клеток. Пространство состояний описывается морфологическими признаками архетипов зоологических систематик.
5) В экологии сообществ объект — популяция организмов. Изменчивость складывается из процессов рождения и гибели особей. Пространство состояний — набор всевозможных векторов (n1, n2, ..., ni, ..., nw), где ni — численность популяции вида i, входящего в сообщество. Набор ограничен доступными организмам ресурсами среды.
* ЧАСТНЫЙ СЛУЧАЙ II.
В случае, когда система и связанные с ней обьекты и отношения могут быть описаны с помощью множеств (в виде теоретико-множественной модели), возможно построение пространств состояний, некоторыми из которых являются следующие [104]:
- метрическое пространство отображения классических динамических систем (см. §2.3);
- топологическое пространство, определяемое в явной форме открытыми множествами, обеспечивающее строгое представление интуитивных понятий аппроксимации и непрерывности конкретного класса систем; при этом топологическая структура позволяет получить критерий синтеза систем;
- топологическое пространство оптимизационных задач в экономике;
- топологические структуры моделей в социальной психологии, опирающиеся на понятие связности, границы и непрерывности;
- развитые топологические понятия и методы в теоретической физике.
* ЧАСТНЫЙ СЛУЧАЙ III [137].
"Описывая некоторую содержательную теорию, в принципе возможно построить не одну, а несколько аксиоматических систем, которые отличались бы прежде всего набором исходных принципов. Эти системы соответственно явились бы основой различных формальных моделей одной и той же содержательной теории" [49].
Как и в ЧАСТНОМ СЛУЧАЕ II, предполагается применимость теоретико-множественной модели.
Задается семейство множеств
 , где I — множество индексов, и определяется система, заданная на V, как некоторое собственное подмножество декартова произведения
, где I — множество индексов, и определяется система, заданная на V, как некоторое собственное подмножество декартова произведения
 .
.
Все компоненты  декартова произведения V называются объектами системы S. При этом рассматривается система с двумя объектами — входным объектом X и выходным объектом Y:
декартова произведения V называются объектами системы S. При этом рассматривается система с двумя объектами — входным объектом X и выходным объектом Y:
 .
.
Для построения на базе введенного определения S некоторой теории, необходимо наделить систему, как отношение, некоторой дополнительной структурой. Это предлагается сделать одним из двух способов:
(i) ввести дополнительную структуру для элементов объектов системы, например, рассматривая сам элемент  как некоторое множество с подходящей структурой;
как некоторое множество с подходящей структурой;
(ii) ввести структуру непосредственно для самих объектов системы  .
.
Первый путь приводит к понятию (абстрактных) временных систем, а второй — к понятию алгебраической системы.
(а) Временные системы.
Пусть имеются системы, у которых элементы входного и выходного объектов определены на одном и том же множестве,  . В этом случае под системой понимается отношение
. В этом случае под системой понимается отношение
 ,
,
где T — линейно упорядоченное индексирующее множество для V, или множество моментов времени, A — алфавит объекта V,  (функция),
(функция), 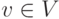 , если все области и кообласти всех функций для данного объекта V одинаковы, т. е. каждая функция
, если все области и кообласти всех функций для данного объекта V одинаковы, т. е. каждая функция 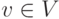 является отображением T в A,
является отображением T в A,  .
.
В более общей ситуации алгебраический объект порождается целым семейством операций. Точнее говоря, объект V задается некоторым множеством элементов W, называемых примитивными, некоторым множеством операций R={R1, ..., Rn} и правилом, согласно которому V содержит, во-первых, все примитивные элементы,  , а, кроме того, и все элементы, которые могут быть порождены из примитивных в результате многократного применения операций из R.
, а, кроме того, и все элементы, которые могут быть порождены из примитивных в результате многократного применения операций из R.
МЕТОДИЧЕСКИЕ ПОЯСНЕНИЯ. В ЧАСТНОМ СЛУЧАЕ III мы изложили начальное определение так называемой "общей теории систем Месаровича", названной нами системной теорией. Являясь абстрактной, эта теория получила развитие в такой же абстрактной теории иерархических многоуровневых систем [139], но ни та, ни другая не получили развитие в прикладных науках (см., например, "Прикладная общая теория систем" [43]). Мы уже отмечали недостаточную общность системных теорий для того, чтобы служить общей теорией систем. Дополнительно отметим примитивность содержательного обоснования теоретико-множественных системных теорий. "Практика нуждается в простых моделях, базирующихся на нетривиальных посылках. Между тем, сегодня наука обычно создает сложные модели, базирующиеся на посылках содержательно бедных" [116]. Тем не менее, множественные модели являются достаточно общими, наглядными и, зачастую, безальтернативными. В частности, нам необходимо: найти общие пути интерпретации базиса топологического пространства М, найти способы отображения в М функций систем и др.
