|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы с открытыми ключами
Атака методом цепных дробей
См. [1]
В целях ускорения зашифрования и расшифрования в системе RSA часто открытый или секретный показатель выбирают малыми. Поскольку размеры чисел составляют сотни бит, сокращение длины показателей первоначально могло выглядеть обоснованным. Однако такой способ увеличения скорости шифрования часто приводит к снижению стойкости.
Теорема 8.1 (Винер) Пусть в системе RSA выполняются неравенства  и
и ![d<\dfrac{1}{3}\sqrt[{4}]{n}](/sites/default/files/tex_cache/1276aa2c7d9df25082421958d67ce290.png) . Тогда по открытому ключу
. Тогда по открытому ключу  можно вычислить секретный показатель
можно вычислить секретный показатель  .
.
При некотором целом  выполняется неравенство:
выполняется неравенство:
![\left|\frac{e}{n}-\frac{k}{d}\right|\leq \frac{1}{d\sqrt[4]{n}} < \frac{1}{2d^2}.](/sites/default/files/tex_cache/5d10cb60ecd3ee56bbd94e97ce2f605e.png)
Число дробей  , для которых
, для которых  , удовлетворяющих полученому соотношению, не превосходит
, удовлетворяющих полученому соотношению, не превосходит  , и все они являются подходящими дробями
, и все они являются подходящими дробями  к рациональному чилу
к рациональному чилу  . Для некоторого
. Для некоторого  будет выполняться равенство
будет выполняться равенство  . Из равенства
. Из равенства  следует, что числа
следует, что числа  и
и  взаимно просты, значит,
взаимно просты, значит,  ,
,  .
.
Пример 8.7 Пусть  - открытый ключ. Найдём
- открытый ключ. Найдём  .
.
Раскладываем число  в цепную дробь и находим последовательно подходящие дроби:
в цепную дробь и находим последовательно подходящие дроби:
![\begin{align*}\frac{2693216516134636609}{4617790059809965777}=[0;1,1,2,1,1,64,3,1,1,61,2,9,\ldots],\\
\frac{P_1}{Q_1} =\frac{1}{1};\quad \frac{P_2}{Q_2} =\frac{1}{2};\quad \frac{P_3}{Q_3} =\frac{3}{5};\quad \frac{P_4}{Q_4} =\frac{4}{7};\quad \frac{P_5}{Q_5} =\frac{7}{12};\\
\frac{P_6}{Q_6} =\frac{452}{775};\quad \frac{P_7}{Q_7} =\frac{1363}{2337};\quad \frac{P_8}{Q_8} =\frac{1815}{3112};\quad
\frac{P_9}{Q_9} =\frac{3178}{5449}.\end{align*}](/sites/default/files/tex_cache/0c35a8d53ad38edc5d6c6afabccf3f74.png)
Для девятой подходящей дроби получаем, что разность  делится нацело на
делится нацело на  :
:

Полагаем  . Секретный ключ найден.
. Секретный ключ найден.
Атака повторным шифрованием
Строим последовательность:  ,
,  ,
,  . Итак,
. Итак,  , а так как
, а так как  , то существует такое натуральное число
, то существует такое натуральное число  , что
, что  . Но тогда
. Но тогда  , отсюда следует, что
, отсюда следует, что  , значит,
, значит,  - решение сравнения
- решение сравнения  .
.
Пример 8.8 Пусть у нас имеется открытый ключ  ,
,  и зашифрованное им сообщение
и зашифрованное им сообщение  . Найдём открытый текст
. Найдём открытый текст  .
.
Возводя  в степень
в степень  , строим последовательность:
, строим последовательность:

Следовательно, 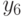 является решением сравнения
является решением сравнения  , а, следовательно, искомым сообщением
, а, следовательно, искомым сообщением  .
.
Замечание. Анализ метода повторного шифрования хорошо показывает необходимость соблюдения требований на выбор  и
и  для обеспечения стойкости. В данном примере
для обеспечения стойкости. В данном примере  . Неудачный выбор криптосистемы привел к тому, что атака методом повторного шифрования дала результат почти сразу, тогда как нахождение
. Неудачный выбор криптосистемы привел к тому, что атака методом повторного шифрования дала результат почти сразу, тогда как нахождение  потребовало бы на порядок больших вычислений.
потребовало бы на порядок больших вычислений.
Атака на основе Китайской теоремы об остатках
Как отмечалось ранее, системы шифрования с открытыми ключами работают сравнительно медленно. Для повышения скорости шифрования RSA на практике используют малую экспоненту зашифрования.
Если выбрать число  небольшим или таким, чтобы в его двоичной записи было мало единиц, то процедуру шифрования можно значительно ускорить. Например, выбрав
небольшим или таким, чтобы в его двоичной записи было мало единиц, то процедуру шифрования можно значительно ускорить. Например, выбрав  (при этом ни
(при этом ни  , ни
, ни  не должны делиться на 3), мы сможем реализовать шифрование с помощью одного возведения в квадрат по модулю
не должны делиться на 3), мы сможем реализовать шифрование с помощью одного возведения в квадрат по модулю  и одного перемножения. Выбрав
и одного перемножения. Выбрав  - число, двоичная запись которого содержит только две единицы, мы сможем реализовать шифрование с помощью 16 возведений в квадрат по модулю
- число, двоичная запись которого содержит только две единицы, мы сможем реализовать шифрование с помощью 16 возведений в квадрат по модулю  и одного перемножения. Если экспонента
и одного перемножения. Если экспонента  выбирается случайно, то реализация шифрования по алгоритму RSA потребует
выбирается случайно, то реализация шифрования по алгоритму RSA потребует  возведений в квадрат по модулю
возведений в квадрат по модулю  и в среднем
и в среднем  умножений по тому же модулю, где
умножений по тому же модулю, где  - длина двоичной записи числа
- длина двоичной записи числа  .
Вместе с тем, выбор небольшой экспоненты
.
Вместе с тем, выбор небольшой экспоненты  может привести к негативным последствиям. Дело в том, что у нескольких корреспондентов могут оказаться одинаковые экспоненты
может привести к негативным последствиям. Дело в том, что у нескольких корреспондентов могут оказаться одинаковые экспоненты  .
.
Пусть, например, три корреспондента имеют попарно взаимно простые модули 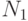 ,
, 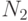 ,
,  и общую экспоненту
и общую экспоненту  . Если еще один пользователь посылает им некое циркулярное сообщение
. Если еще один пользователь посылает им некое циркулярное сообщение  , то криптоаналитик противника может получить в свое распоряжение три шифрованных текста
, то криптоаналитик противника может получить в свое распоряжение три шифрованных текста  ,
, 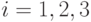 . Далее, он может найти решение системы сравнений, лежащее в интервале
. Далее, он может найти решение системы сравнений, лежащее в интервале  и удовлетворяющее уравнениям:
и удовлетворяющее уравнениям:

По китайской теореме об остатках такое решение  единственно, а так как
единственно, а так как  , то
, то  . Значение
. Значение  можно найти, вычислив кубический корень
можно найти, вычислив кубический корень ![x=\sqrt[3]{y}](/sites/default/files/tex_cache/792d1c3ee23e28c1e0d0e3ec30bb379f.png) . Отметим, 8.1 что выбор малой экспоненты расшифрования
. Отметим, 8.1 что выбор малой экспоненты расшифрования  также нежелателен в связи с возможностью определения
также нежелателен в связи с возможностью определения  простым перебором. Известно также что если
простым перебором. Известно также что если ![d<\sqrt[4]{N}](/sites/default/files/tex_cache/c616a7e07cb120570f03798c54513a14.png) , то экспоненту
, то экспоненту  легко найти, используя непрерывные дроби.
легко найти, используя непрерывные дроби.
Пример 8.9 Три пользователя имеют модули  ,
,  ,
,  . Все пользователи используют экспоненту
. Все пользователи используют экспоненту  . Всем пользователям было послано некое сообщение
. Всем пользователям было послано некое сообщение  , причем пользователи получили сообщения
, причем пользователи получили сообщения  ,
,  ,
,  . Найдём
. Найдём  .
.
С помощью китайской теоремы об остатках решим систему:

Для этого вычислим  . Далее находим
. Далее находим
Отсюда ![x=\sqrt[3]{1000000000} = 1000](/sites/default/files/tex_cache/988ac01de7189de1d4858277bcf1335a.png) - исходное сообщение, отправленное пользователям.
- исходное сообщение, отправленное пользователям.
Бесключевое чтение
Пусть два пользователя выбрали одинаковый модуль  и взаимно простые экспоненты
и взаимно простые экспоненты  и
и  . Если один пользователь посылает им некое циркулярное сообщение
. Если один пользователь посылает им некое циркулярное сообщение  , то криптоаналитик противника может получить в свое распоряжение два шифрованных текста
, то криптоаналитик противника может получить в свое распоряжение два шифрованных текста  и
и  . В таком случае криптоаналитик может получить исходное сообщение, найдя с помощью алгоритма Евклида числа
. В таком случае криптоаналитик может получить исходное сообщение, найдя с помощью алгоритма Евклида числа  и
и  такие, что
такие, что  . Отсюда получаем:
. Отсюда получаем:

Пример 8.10 Два пользователя применяют общий модуль  , но разные взаимно простые экспоненты
, но разные взаимно простые экспоненты  и
и  . Пользователи получили шифртексты
. Пользователи получили шифртексты  и
и  , которые содержат одно и то же сообщение. Найдем исходное сообщение методом бесключевого чтения.
, которые содержат одно и то же сообщение. Найдем исходное сообщение методом бесключевого чтения.
Так как  и
и  взаимно просты, то найдем такие
взаимно просты, то найдем такие  и
и  , что
, что  . С помощью расширенного алгоритма Евклида находим
. С помощью расширенного алгоритма Евклида находим  ,
,  . Искомое сообщение:
. Искомое сообщение:

Выводы
Как видно из приведенных выше примеров, выбор параметров криптосистемы является ответственной задачей. Параметры необходимо выбирать в строгом соответствии с требованиями. Существующими в настоящими время методами (и при использовании существующих в настоящее время вычислительных мощностей) атака на алгоритм и/или криптосистему возможна лишь при неудачном выборе параметров. В частности, необходимо обеспечить каждому пользователю уникальные значения  ,
,  и уникальное значение
и уникальное значение  , удовлетворяющие требованиям, приведенным выше.
, удовлетворяющие требованиям, приведенным выше.










