Опубликован: 02.02.2011 | Уровень: для всех | Доступ: платный
Лекция 48:
Задания
Задание 5. Двумерный массив
Решите задачи данной группы, оформив решение в виде функций генерации, вывода и обработки массивов. Предусмотрите в функции генерации массива ввод границ диапазона случайных чисел.
- Дана квадратная матрица порядка
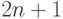 . Зеркально отразить ее элементы относительно горизонтальной оси симметрии матрицы.
. Зеркально отразить ее элементы относительно горизонтальной оси симметрии матрицы. - Даны действительные числа
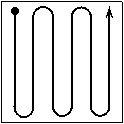
 . Получить действительную квадратную матрицу порядка 8, элементами которой являются числа
. Получить действительную квадратную матрицу порядка 8, элементами которой являются числа  , расположенные в ней по схеме, которая приведена на рисунке.
, расположенные в ней по схеме, которая приведена на рисунке.
- Дана матрица размера
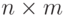 . Поменять местами ее столбцы так, чтобы их максимальные элементы образовывали убывающую последовательность.
. Поменять местами ее столбцы так, чтобы их максимальные элементы образовывали убывающую последовательность. - Найдите квадратную матрицу, обратную данной с размером
 .
. - Дана квадратная матрица порядка
 . Повернуть ее на 180 градусов в положительном направлении.
. Повернуть ее на 180 градусов в положительном направлении. - Заполнить двумерный квадратный массив целыми числами от 1 до 100 по спирали, как показано на следующем рисунке.
- Даны действительные числа
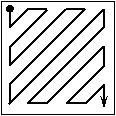
 . Получить действительную квадратную матрицу порядка 8, элементами которой являются числа
. Получить действительную квадратную матрицу порядка 8, элементами которой являются числа  , расположенные в ней по схеме, которая приведена на рисунке.
, расположенные в ней по схеме, которая приведена на рисунке.
- Дана матрица размера
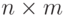 . Поменять местами столбцы, содержащие минимальный и максимальный элементы матрицы.
. Поменять местами столбцы, содержащие минимальный и максимальный элементы матрицы. - Даны две матрицы
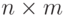 и
и  . Получите их произведение.
. Получите их произведение. - Дана матрица размера
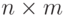 . Поменять местами ее строки так, чтобы их максимальные элементы образовывали возрастающую последовательность.
. Поменять местами ее строки так, чтобы их максимальные элементы образовывали возрастающую последовательность. - В данной действительной квадратной матрице порядка
 найти наибольший по модулю элемент. Получить квадратную матрицу порядка
найти наибольший по модулю элемент. Получить квадратную матрицу порядка  путем выбрасывания из исходной матрицы какой-нибудь строки и столбца, на пересечении которых расположен элемент с найденным значением. Выполняйте до тех пор, пока не останется последний элемент.
путем выбрасывания из исходной матрицы какой-нибудь строки и столбца, на пересечении которых расположен элемент с найденным значением. Выполняйте до тех пор, пока не останется последний элемент. - Дана квадратная матрица порядка
 . Зеркально отразить ее элементы относительно побочной диагонали матрицы.
. Зеркально отразить ее элементы относительно побочной диагонали матрицы. - Дана действительная квадратная матрица порядка
 . Получить новую матрицу, повернув ее блоки, ограниченные диагоналями, на 180 градусов.
. Получить новую матрицу, повернув ее блоки, ограниченные диагоналями, на 180 градусов. - Дана матрица размера
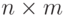 . Поменять местами ее первый и последний строки, содержащие только отрицательные элементы.
. Поменять местами ее первый и последний строки, содержащие только отрицательные элементы. - Дана целочисленная матрица размера
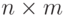 . Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце. Если такой элемент отсутствует, то вывести 0.
. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце. Если такой элемент отсутствует, то вывести 0. - Составьте программу циклической перестановки столбцов двумерного массива
 , при которой смещение происходит вправо на n столбцов.
, при которой смещение происходит вправо на n столбцов. - Даны действительные числа
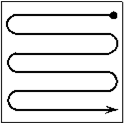
 . Получить действительную квадратную матрицу порядка 8, элементами которой являются числа
. Получить действительную квадратную матрицу порядка 8, элементами которой являются числа  , расположенные в ней по схеме, которая приведена на рисунке.
, расположенные в ней по схеме, которая приведена на рисунке.
- Дана матрица размера
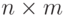 . Поменять местами ее столбцы так, чтобы их минимальные элементы образовывали возрастающую последовательность.
. Поменять местами ее столбцы так, чтобы их минимальные элементы образовывали возрастающую последовательность. - Дана квадратная матрица порядка
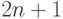 . Зеркально отразить ее элементы относительно вертикальной оси симметрии матрицы.
. Зеркально отразить ее элементы относительно вертикальной оси симметрии матрицы. - Дана квадратная матрица порядка
 . Повернуть ее на 270 градусов в положительном направлении относительно ее центра.
. Повернуть ее на 270 градусов в положительном направлении относительно ее центра. - Дана матрица размера
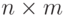 . Поменять местами строки, содержащие минимальный и максимальный элементы матрицы.
. Поменять местами строки, содержащие минимальный и максимальный элементы матрицы. - В квадратной таблице обменяйте местами элементы строки и столбца, на пересечении которых находится минимальный из положительных элементов.
- Дана квадратная матрица порядка
 . Повернуть ее на 90 градусов в положительном направлении относительно ее центра.
. Повернуть ее на 90 градусов в положительном направлении относительно ее центра. - Дана квадратная матрица порядка
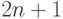 . Зеркально отразить ее элементы относительно главной диагонали матрицы.
. Зеркально отразить ее элементы относительно главной диагонали матрицы. - Составьте программу циклической перестановки строк двумерного массива
 , при которой смещение происходит вниз на
, при которой смещение происходит вниз на  .
. - Дана матрица размера
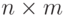 . Поменять местами ее первый и последний столбцы, содержащие только положительные элементы.
. Поменять местами ее первый и последний столбцы, содержащие только положительные элементы. - Заполнить двумерный квадратный массив целыми числами от 1 до 100 по спирали, начиная от центра и закручивая по часовой стрелке.
- Заполните квадратную матрицу
 по принципу латинского квадрата: в каждой строке и каждом столбце используются неповторяющиеся между собой числа от 1 до
по принципу латинского квадрата: в каждой строке и каждом столбце используются неповторяющиеся между собой числа от 1 до  .
.