|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Машины Тьюринга
Частично-рекурсивные функции
Пытаясь выяснить содержание интуитивного понятия вычислимой функции,
А.Черч в 1936 году рассмотрел класс так называемых рекурсивных функций,
а Клини расширил его до класса частично-рекурсивных функций. В то же время
впервые была высказана естественно-научная гипотеза о том, что интуитивное
понятие вычислимой частичной функции совпадает с понятием частично
рекурсивной функции. Эту гипотезу называют тезисом Черча. Здесь мы
напомним понятие частично-рекурсивной функции и покажем, что любая
частично-рекурсивная функция вычислима по Тьюрингу.
Набор аргументов  обозначим через
обозначим через 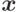 .
.
Функция 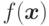 называется суперпозицией
называется суперпозицией  -местных
функций
-местных
функций 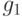 ,
, 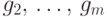 и
и  -местной
функции
-местной
функции  , если
, если 
Говорят, что 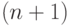 -местная функция
-местная функция 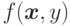 получена примитивной
рекурсией из
получена примитивной
рекурсией из 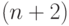 -местной функции
-местной функции  и
и  -местной функции
-местной функции  , если
, если
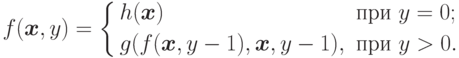
Говорят, что  -местная функция
-местная функция 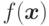 получена минимизацией из
получена минимизацией из  -местной функции
-местной функции  , если
, если

Часто обозначают 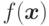 через
через 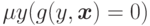 .
.
Заметим, что суперпозиция и примитивная рекурсия, примененные к всюду определенным функциям, дают всюду определенные функции, тогда как минимизация, примененная к всюду определенной функции, может дать частичную функцию.
Числовая функция 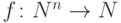 называется частично
рекурсивной, если она является одной из базисных функций:
называется частично
рекурсивной, если она является одной из базисных функций:
а) 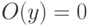 (при всех
(при всех 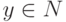 ),
),
б) 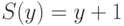 (при всех
(при всех 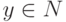 ),
),
в) 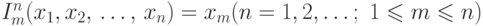
или получена из них с помощью конечного числа применений суперпозиции, примитивной рекурсии и минимизации.
Теорема. Любая частично-рекурсивная функция вычислима по Тьюрингу.
Доказательство теоремы заключено в следующих четырех леммах, с использованием унарного кодирования чисел.
Лемма 1 (о базисных функциях).
Базисные функции 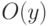 ,
, 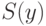 ,
, 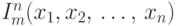 вычислимы по Тьюрингу.
вычислимы по Тьюрингу.
Действительно, функцию 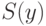 вычисляет программа
вычисляет программа ![[K_m, 1,
r]](/sites/default/files/tex_cache/d3d376c62fb446440d1b80b97172ac0d.png) , функцию
, функцию 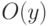 — программа
— программа ![[r]](/sites/default/files/tex_cache/c67bae384c19ebaf9ce07de893add5c8.png) , функцию
, функцию 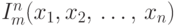 — программа
— программа 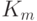 .
.
Лемма 2 (о суперпозиции).
Если функции 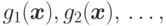
 и
и 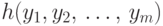 вычислимы, соответственно, программами
вычислимы, соответственно, программами 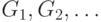 ,
,  и
и  ,
то функцию
,
то функцию
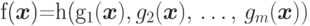
![\eq*{
[G_m, (Z_{n + 1})^n, G_{{m}-1}, (Z_{n + 1})^n\dts
G_1, (Z_{n + 1})^n, (Z_{n + m})^{n}, H, (\Lambda_2)^m].
}](/sites/default/files/tex_cache/a8f41a7fc6ade1f1a639f665de85a80a.png)
Доказательство. Чтобы убедиться в справедливости этого утверждения, достаточно выписать псевдослова, которые появляются на ленте после выполнения отдельных частей программы. Сначала на ленте находится псевдослово

после выполнения  на ленте будет
на ленте будет

после ![[G_m, (Z_{n + 1})^n]](/sites/default/files/tex_cache/48198b4e21e6d43e4b1a999bb1f73154.png) —
—

после ![[G_m, (Z_{n + 1})^n, G_{{m}-1}]](/sites/default/files/tex_cache/94caa2ac13464d0130ceb495dc91a2a8.png) —
—

и т.д.
После ![[G_m, (Z_{n + 1})^n, G_{{m}-1}, (Z_{n + 1})^n\dts
G_1, (Z_{n + 1})^n]](/sites/default/files/tex_cache/a70bb32fe7b440c45aa4b9d54ac9aa58.png) —
—
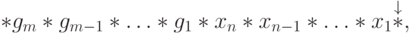
![[G_m, (Z_{n + 1})^n, G_{m-1}, (Z_{n+1})^n \dts G_1,
(Z_{n+1})^n, (Z_{n+m})^n, H]](/sites/default/files/tex_cache/9e2cc40fa0f6724abf1ef65f4bb1dd3d.png) —
—
и, наконец, после выполнения всей программы получим
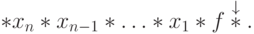
Лемма 3 (о примитивной рекурсии).
Если функции 
 ,
,  и
и 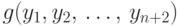 вычислимы соответственно
программами
вычислимы соответственно
программами  и
и  , то функция
, то функция 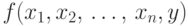 ,
полученная по схеме примитивной рекурсии, вычислима программой
,
полученная по схеме примитивной рекурсии, вычислима программой
![\eq*{
[H, L^{n+1}, l, (\t{пока}\ 1)[\ast, R_{n+2}, G, \Lambda_2,
L_{n+2},1, l], R^{n+2}].
}](/sites/default/files/tex_cache/9d195856271767fb25451c321844e7a9.png)
Доказательство.
Представим программу, предлагаемую для вычисления
функции 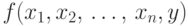 , блок-схемой, изображенной на рисунке.
, блок-схемой, изображенной на рисунке.
Пунктирными стрелками показаны контрольные дуги, для которых будут
сформированы соответствующие индуктивные утверждения  .
.
Утверждение  соответствует входной дуге и поэтому должно
описывать содержимое ленты в начальный момент. Утверждение
соответствует входной дуге и поэтому должно
описывать содержимое ленты в начальный момент. Утверждение  соответствует
выходной дуге и должно описывать содержимое ленты в момент завершения
работы программы. Утверждение
соответствует
выходной дуге и должно описывать содержимое ленты в момент завершения
работы программы. Утверждение  относится к дуге, разрезающей
единственный имеющейся в блок-схеме цикл, поэтому должно быть
сформулировано так, чтобы ему удовлетворяло содержимое ленты каждый раз,
когда в программе реализуется переход по рассматриваемой дуге.
относится к дуге, разрезающей
единственный имеющейся в блок-схеме цикл, поэтому должно быть
сформулировано так, чтобы ему удовлетворяло содержимое ленты каждый раз,
когда в программе реализуется переход по рассматриваемой дуге.
Напомним, что основное требование, предъявляемое к утверждениям 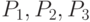 , заключается в том, чтобы была возможность
доказательства индуктивных шагов:
, заключается в том, чтобы была возможность
доказательства индуктивных шагов:
![\eqa*{ & P_1 \to P_2,\ \t{если реализуется путь}\ [H; L^{n+1}; l; \ast;
R^{n+2}; G];\\ & P_1 \to P_3,\ \t{если реализуется путь}\ [H; L_{n+1}; l;
R^{n+2}];\\ & P_2 \to P_2,\ \t{если реализуется путь}\ [\Lambda_2;
L^{n+2}; 1; l; \ast; R^{n+2}; G];\\ & P_2 \to P_3,\ \t{если реализуется
путь}\
[\Lambda_2; L_{n+2}; 1; l; R_{n+2}].
}](/sites/default/files/tex_cache/bd7afa475d3ec80081bd3c6d81bfe770.png)
Пусть  ,
,  — исходные
значения аргументов из множества
— исходные
значения аргументов из множества  , тогда требуемые утверждения можно
сформулировать следующим образом:
, тогда требуемые утверждения можно
сформулировать следующим образом:
P_1 — содержимое ленты равно
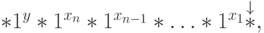
 — существует
— существует 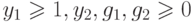 такие, что содержимое ленты равно
такие, что содержимое ленты равно

 — содержимое ленты равно
— содержимое ленты равно
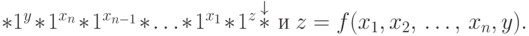
Доказательство индуктивных шагов легко получить, выписывая содержимое ленты после каждого оператора в соответствующем пути. Читателю предоставляется возможность проделать это самостоятельно и убедиться в правильности программы, предлагаемой в формулировке леммы 3. Не забудьте доказать завершаемость исследуемой программы.
Лемма 4 (о минимизации).
Если функция 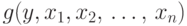 вычислима
программой
вычислима
программой  ,
то функция
,
то функция 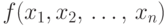 , полученная из нее по схеме
минимизации, вычисляется программой
, полученная из нее по схеме
минимизации, вычисляется программой
![\eq*{
[r, G, l, (\t{пока}\ 1)[r, \Lambda_1, 1, r, G, l].
}](/sites/default/files/tex_cache/3cc62406efe9b27b8d47e43e1f453a53.png)
Доказательство.
Представим программу, предлагаемую для вычисления
функции 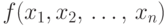 , блок-схемой
c указанными контрольными точками
, блок-схемой
c указанными контрольными точками  ,
,  ,
,  .
.
Пусть  — исходные значения
аргументов, тогда для доказательства частичной корректности предлагаемой
программы можно воспользоваться следующими индуктивными утверждениями:
— исходные значения
аргументов, тогда для доказательства частичной корректности предлагаемой
программы можно воспользоваться следующими индуктивными утверждениями:
 — содержимое ленты равно
— содержимое ленты равно
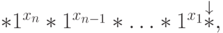
 — существуют
— существуют  , такие, что
содержимое ленты равно
, такие, что
содержимое ленты равно
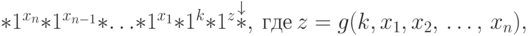
 — содержимое ленты равно
— содержимое ленты равно

![\eqa*{ & P_1 \to P_2,\ \t{если реализуется путь}\ [r, G];\\ & P_2 \to
P_2,\ \t{если реализуется путь}\ [l; r; \Lambda_1; 1; r; G];\\ & P_2 \to
P_3,\ \t{если реализуется путь}\ [l],\ \t{и головка
остановится на}\\ & \qq \t{символе}\ \ast.
}](/sites/default/files/tex_cache/7e6779e8b66293e1bca029c1844f3c08.png)
Доказательство индуктивных утверждений и завершаемости программы мы оставляем читателю в качестве упражнений.
Заметим, что в доказательствах лемм 3 и 4 при рисовании блок-схемы мы несущественно отступили от текстов программ, данных в их формулировках, а при доказательстве леммы 2 не выписывали индуктивных утверждений, так как в представлении программы блок-схемой нет циклов. Обращаем внимание на то, что правильность блоков, из которых составлены программы, мы не подвергаем сомнению.


