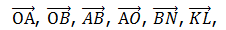Геометрия: координаты, фигуры

Движение и вектор на плоскости

Вектор и движение

Теория

Разность точек. Точка на прямой соответствует числу. Мы даже говорим, что точка на прямой – это и есть число.

Точка на плоскости соответствует своим координатам - паре чисел. Мы говорим, что точка это и есть пара чисел.

Разность точек на оси – вектор на оси – это число. Может смотреть вперед, если его координата положительная и назад, если его координата отрицательная.

Вектор на плоскости – это два числа. Это тоже разность точек. Разность определяется покоординатно:

Вектор (ML) (см рис. 2.2) и имеет координаты: координаты точки L минус координаты точки M:

Смотрите, вектор (LK) пошел вперед и вниз. Вниз – это и означает, что его координата Y отрицательная.

Найти величину вектора

Задачи на бумаге

Найдите разность точек, нарисуйте вектор разности

найдите его значение

Мышка на плоскости

Практическое занятие: "координаты на плоскости"

Плоскость в скретч: координаты Х от -240 до +240, Y -180 до +180

Устанавливаем мышку – чтобы добежать до сыра, смотрим координаты

Подвигаем мышку стрелками вправо-влево, вверх-вниз.

Как меняются координаты мышки?

Дополните таблицу.

Задачи на вектор

Задачи на бумаге

Нарисовать и найти значение векторов между точками пп. 3.4.2

Проверка знаний

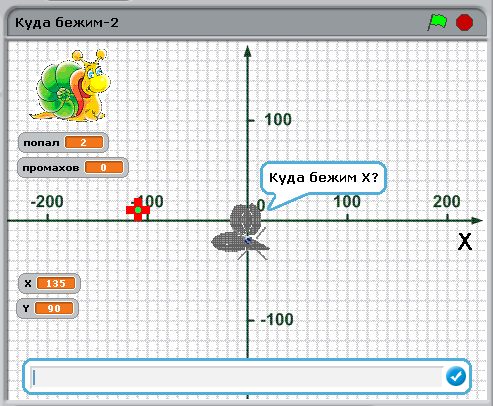
Игра-задача Куда бежим-2

Игра похожа на игру "куда бежим 1", но уже на координатной плоскости:

1. Запустить игру, нажав на зеленый флажок
2. Мышка спросит "куда бежим X?", а потом "куда бежим Y?". Наши ответы мы видим в переменных X и Y в левом нижнем углу игрового поля.
3. Нужно ответить, куда надо сдвинуть мышку, чтобы она попала на мишень. Для этого надо вычесть из координаты мишени координаты мышки.
4. Теперь мышка бежит к мишени и рисует свой путь – это и есть изображение нашего вектора движения.
5. Теперь мышка бежит к мишени и рисует свой путь – это и есть изображение нашего вектора движения.