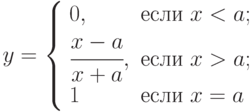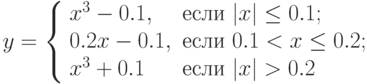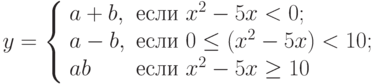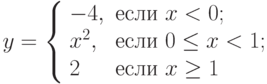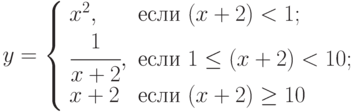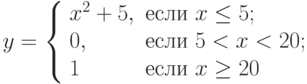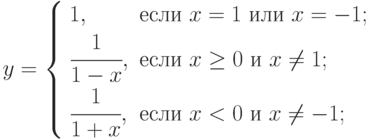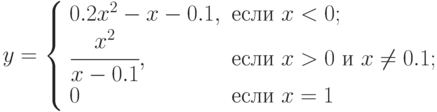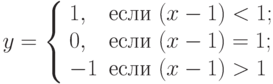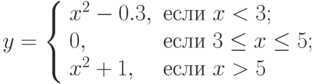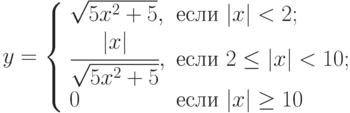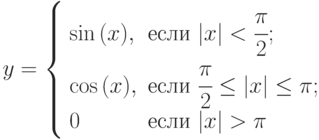| Россия |
Опубликован: 19.02.2009 | Уровень: специалист | Доступ: платный
Лекция 5:
Методы: основные понятия
Практикум
- Решение простейших задач:
- Разработать метод
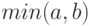 для нахождения минимального из двух чисел. Вычислить с помощью него значение выражения
для нахождения минимального из двух чисел. Вычислить с помощью него значение выражения 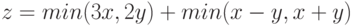 .
.Пример.
using System; namespace Hello { class Program { static double min(double a, double b) { return (a < b) ? a : b; } static void Main(string[] args) { Console.Write("x="); double x = double.Parse(Console.ReadLine()); Console.Write("y="); double y = double.Parse(Console.ReadLine()); double z = min(3 * x, 2 * y) + min(x - y, x + y); Console.WriteLine("z=" + z); } } } - Разработать метод
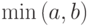 для нахождения минимального из двух чисел. Вычислить с помощью него минимальное значение из четырех чисел
для нахождения минимального из двух чисел. Вычислить с помощью него минимальное значение из четырех чисел  ,
,  ,
,  ,
,  .
. - Разработать метод
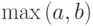 для нахождения максимального из двух чисел. Вычислить с помощью него значение выражения
для нахождения максимального из двух чисел. Вычислить с помощью него значение выражения 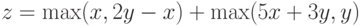 .
. - Разработать метод
 , который вычисляет значение по следующей формуле:
, который вычисляет значение по следующей формуле: 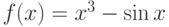 . Определить, в какой из точек
. Определить, в какой из точек  или
или  , функция принимает наибольшее значение.
, функция принимает наибольшее значение. - Разработать метод
 , который вычисляет значение по следующей формуле:
, который вычисляет значение по следующей формуле:  . Определить, в какой из точек а или b, функция принимает наименьшее значение.
. Определить, в какой из точек а или b, функция принимает наименьшее значение. - Разработать метод
 , который возвращает младшую цифру натурального числа
, который возвращает младшую цифру натурального числа  . Вычислить с помощью него значение выражения
. Вычислить с помощью него значение выражения 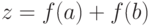 .
. - Разработать метод
 , который возвращает вторую справа цифру натурального числа
, который возвращает вторую справа цифру натурального числа  . Вычислить с помощью него значение выражения
. Вычислить с помощью него значение выражения 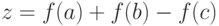 .
. - Разработать метод
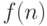 , который для заданного натурального числа n находит значение
, который для заданного натурального числа n находит значение  .
Вычислить с помощью него значение выражения
.
Вычислить с помощью него значение выражения  .
. - Разработать метод
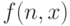 , который для заданного натурального числа n и вещественного х находит значение выражения
, который для заданного натурального числа n и вещественного х находит значение выражения  .
Вычислить с помощью данного метода значение выражения
.
Вычислить с помощью данного метода значение выражения 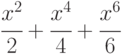 .
. - Разработать метод
 , который нечетное число заменяет на
, который нечетное число заменяет на  , а четное число уменьшает в два раза. Продемонстрировать работу данного метода на примере.
, а четное число уменьшает в два раза. Продемонстрировать работу данного метода на примере. - Разработать метод
 , который число, кратное
, который число, кратное 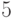 , уменьшает в
, уменьшает в 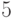 раз, а остальные числа увеличивает на
раз, а остальные числа увеличивает на  . Продемонстрировать работу данного метода на примере.
. Продемонстрировать работу данного метода на примере. - Разработать метод
 , который в двузначном числе меняет цифры местами, а остальные числа оставляет без изменения. Продемонстрировать работу данного метода на примере.
, который в двузначном числе меняет цифры местами, а остальные числа оставляет без изменения. Продемонстрировать работу данного метода на примере. - Разработать метод
 , который в трехзначном числе меняет местами первую с последней цифрой, а остальные числа оставляет без изменения. Продемонстрировать работу данного метода на примере.
, который в трехзначном числе меняет местами первую с последней цифрой, а остальные числа оставляет без изменения. Продемонстрировать работу данного метода на примере. - Разработать метод
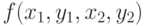 , который вычисляет длину отрезка по координатам вершин
, который вычисляет длину отрезка по координатам вершин  и
и 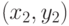 , и метод
, и метод 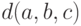 , который вычисляет периметр треугольника по длинам сторон
, который вычисляет периметр треугольника по длинам сторон  ,
,  ,
,  . С помощью данных методов найти периметр треугольника, заданного координатами своих вершин.
. С помощью данных методов найти периметр треугольника, заданного координатами своих вершин. - Разработать метод
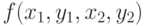 , который вычисляет длину отрезка по координатам вершин (x_{1}, y_{1}) и
, который вычисляет длину отрезка по координатам вершин (x_{1}, y_{1}) и 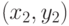 , и метод
, и метод 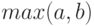 , который вычисляет максимальное из чисел
, который вычисляет максимальное из чисел  ,
,  . С помощью данных методов определить, какая из трех точек на плоскости наиболее удалена от начала координат.
. С помощью данных методов определить, какая из трех точек на плоскости наиболее удалена от начала координат. - Разработать метод
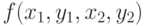 , который вычисляет длину отрезка по координатам вершин
, который вычисляет длину отрезка по координатам вершин  и
и 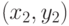 , и метод
, и метод 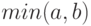 , который вычисляет минимальное из чисел
, который вычисляет минимальное из чисел  ,
,  . С помощью данных методов найти две из трех заданных точек на плоскости, расстояние между которыми минимально.
. С помощью данных методов найти две из трех заданных точек на плоскости, расстояние между которыми минимально. - Разработать метод
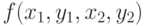 , который вычисляет длину отрезка по координатам вершин
, который вычисляет длину отрезка по координатам вершин  и
и 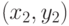 , и метод t(a, b, c), который проверяет, существует ли треугольник с длинами сторон
, и метод t(a, b, c), который проверяет, существует ли треугольник с длинами сторон  ,
,  ,
,  . С помощью данных методов проверить, можно ли построить треугольник по трем заданным точкам на плоскости.
. С помощью данных методов проверить, можно ли построить треугольник по трем заданным точкам на плоскости. - Разработать метод
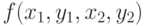 , который вычисляет длину отрезка по координатам вершин
, который вычисляет длину отрезка по координатам вершин  и
и 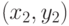 , и метод
, и метод 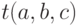 , который проверяет, существует ли треугольник с длинами сторон
, который проверяет, существует ли треугольник с длинами сторон 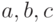 . С помощью данных методов проверить, сколько различных треугольников можно построить по четырем заданным точкам на плоскости.
. С помощью данных методов проверить, сколько различных треугольников можно построить по четырем заданным точкам на плоскости.
- Разработать метод
- Постройте таблицу значений функции
 для
для ![х \in [a, b]](/sites/default/files/tex_cache/17323e8b6cbe81ed05d94ebb28fa6e16.png) с шагом
с шагом  .
.Замечание. Для решения задачи использовать вспомогательный метод.
-
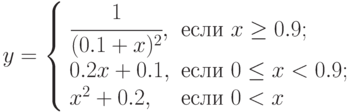
Пример:
using System; namespace Hello { class Program { static double f (double x) { double y; if (x >= 0.9) y = 1 / Math.Pow(1 + x, 2); else if (x >= 0) y = 0.2 * x + 0.1; else y = x * x + 0.2; return y; } static void Main(string[] args) { Console.Write("a="); double a = double.Parse(Console.ReadLine()); Console.Write("b="); double b = double.Parse(Console.ReadLine()); Console.Write("h="); double h = double.Parse(Console.ReadLine()); for (double i = a; i <= b; i += h) Console.WriteLine("f({0:f2})={1:f4}", i, f(i)); } } }
-
- Перегрузите метод
 из предыдущего раздела так, чтобы его сигнатура (заголовок) соответствовала виду static void f (double x, out double y). Продемонстрируйте работу перегруженных методов.
из предыдущего раздела так, чтобы его сигнатура (заголовок) соответствовала виду static void f (double x, out double y). Продемонстрируйте работу перегруженных методов.

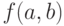 , который по катетам
, который по катетам 
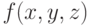 , который по длинам сторон треугольника
, который по длинам сторон треугольника 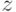 вычисляет его площадь. С помощью данного метода по заданным вещественным числам
вычисляет его площадь. С помощью данного метода по заданным вещественным числам  ,
,  ,
,  найти площадь пятиугольника, изображенного на рисунке.
найти площадь пятиугольника, изображенного на рисунке.