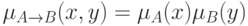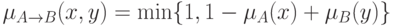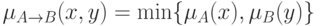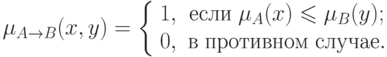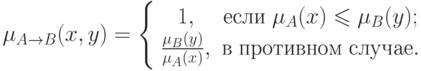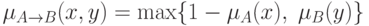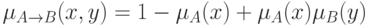|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Теория приближенных рассуждений
Правило modus ponens как частный случай композиционного правила вывода
Как мы увидим ниже, правило modus ponens можно рассматривать как частный случай композиционного правила вывода. Чтобы установить эту связь, мы сперва обобщим понятие материальной импликации с пропозициональными переменными на нечеткие множества.
Пусть  и
и  — нечеткие высказывания и
— нечеткие высказывания и 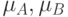 —
соответствующие им функции принадлежности. Тогда импликации
—
соответствующие им функции принадлежности. Тогда импликации 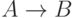 будет соответствовать некоторая функция принадлежности
будет соответствовать некоторая функция принадлежности 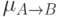 .
По аналогии с традиционной логикой, можно предположить, что
.
По аналогии с традиционной логикой, можно предположить, что

Тогда
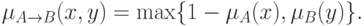
Однако, это не единственное обобщение оператора импликации. В следующей таблице показаны различные интерпретации этого понятия.
Определим теперь обобщенное правило modus ponens (generalized modus ponens).
Приведенная формулировка имеет два отличия от традиционной формулировки
правила modus ponens : во-первых, здесь допускается, что 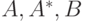 —
нечеткие множества, и, во-вторых,
—
нечеткие множества, и, во-вторых, 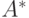 необязательно идентично
необязательно идентично  .
.
Нечеткие экспертные системы
Логико-лингвистические методы описания систем основаны на том, что поведение исследуемой системы описывается в естественном (или близком к естественному) языке в терминах лингвистических переменных. Входные и выходные параметры системы рассматриваются как лингвистические переменные, а качественное описание процесса задается совокупностью высказываний следующего вида:
L1 если A11 и/или A2 и/или ... и/или A1m, то B11 и/или ... и/или B1n,
L2 если A21 и/или A22 и/или ... и/или A2m, то B21 и/или ... и/или B2n,
.....................
Lk если Ak1 и/или Ak2 и/или ... и/или Akm, то Bk1 и/или ... и/или Bkn,
где  ,
, 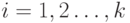
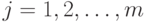 — нечеткие высказывания,
определенные на значениях входных лингвистических переменных, а
— нечеткие высказывания,
определенные на значениях входных лингвистических переменных, а 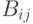 ,
, 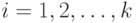
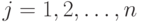 — нечеткие высказывания, определенные на
значениях
выходных лингвистических переменных. Эта совокупность правил носит название
нечеткой базы знаний.
— нечеткие высказывания, определенные на
значениях
выходных лингвистических переменных. Эта совокупность правил носит название
нечеткой базы знаний.
Подобные вычисления составляют основу нечетких экспертных систем. Каждая нечеткая экспертная система использует нечеткие утверждения и правила.
Затем с помощью операторов вычисления дизъюнкции и конъюнкции описание системы можно привести к виду
L1: если А1, то B1,
L2: если А2, то B2,
.....................
Lk: если Аk, то Bk,
где 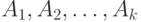 — нечеткие множества, заданные на
декартовом
произведении
— нечеткие множества, заданные на
декартовом
произведении  универсальных множеств входных лингвистических
переменных, а
универсальных множеств входных лингвистических
переменных, а 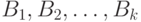 — нечеткие множества,
заданные на декартовом произведении
— нечеткие множества,
заданные на декартовом произведении  универсальных множеств
выходных лингвистических переменных.
универсальных множеств
выходных лингвистических переменных.
В основе построения логико-лингвистических систем лежит рассмотренное выше композиционное правило вывода Заде.
Преимущество данной модели - в ее универсальности. Нам неважно, что
именно на входе — конкретные числовые значения или некоторая
неопределенность,
описываемая нечетким множеством. Но за данную универсальность приходится
расплачиваться сложностью системы — нам приходится работать в
пространстве
размерности  . Поэтому этой общей моделью на практике
пользуются
довольно редко. Обычно же используют ее упрощенный вариант, называемый
нечетким выводом. Он основывается на предположении, что все входные
лингвистические переменные имеют известные нам числовые значения (как и бывает
довольно часто на практике). Также обычно не используют более одной
выходной лингвистической переменной.
. Поэтому этой общей моделью на практике
пользуются
довольно редко. Обычно же используют ее упрощенный вариант, называемый
нечетким выводом. Он основывается на предположении, что все входные
лингвистические переменные имеют известные нам числовые значения (как и бывает
довольно часто на практике). Также обычно не используют более одной
выходной лингвистической переменной.
Нечетким логическим выводом (fuzzy logic inference) называется
аппроксимация зависимости 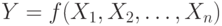 каждой
выходной лингвистической переменной от входных лингвистических
переменных и получение заключения в виде нечеткого множества,
соответствующего текущим значениям входов, с использованием нечеткой
базы знаний и нечетких операций. Основу нечеткого логического вывода
составляет композиционное правило Заде.
каждой
выходной лингвистической переменной от входных лингвистических
переменных и получение заключения в виде нечеткого множества,
соответствующего текущим значениям входов, с использованием нечеткой
базы знаний и нечетких операций. Основу нечеткого логического вывода
составляет композиционное правило Заде.