|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Методы построения функции принадлежности. Обзор основных методов
Косвенные методы для группы экспертов
А.П.Шер предлагает способ определения функции принадлежности на
основе интервальных оценок. Пусть интервал ![[x_{ji} ,x_{ji}^\prime
]](/sites/default/files/tex_cache/1d3c8fdc644823a7a0b5e8fd7bade290.png) отражает
мнение
отражает
мнение  -го эксперта,
-го эксперта,  (
( 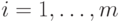 ), о значении
), о значении  -го
(
-го
( 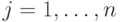 )
признака оцениваемого понятия
)
признака оцениваемого понятия  . Тогда полным описанием этого
понятия
. Тогда полным описанием этого
понятия  -м
экспертом является гиперпараллелепипед
-м
экспертом является гиперпараллелепипед ![\theta _i = [x_{1i}
,x_{1i}^\prime ] \times \ldots \times [x_{ni} ,x_{ni}^\prime ]](/sites/default/files/tex_cache/dbd975254cec70b17543b9e63c40acca.png) .
Приводится процедура, позволяющая вычислять коэффициенты компетентности
экспертов, а также
сводить исходную "размытую" функцию (усредненные экспертные
оценки) к характеристической функции неразмытого, четкого множества.
Алгоритм следующий:
.
Приводится процедура, позволяющая вычислять коэффициенты компетентности
экспертов, а также
сводить исходную "размытую" функцию (усредненные экспертные
оценки) к характеристической функции неразмытого, четкого множества.
Алгоритм следующий:
- Рассматривая для каждого признака
 все интервалы, предложенные экспертами, находим связанное
покрытие их объединения, состоящее из непересекающихся интервалов,
концами которых являются только концы исходных интервалов:
все интервалы, предложенные экспертами, находим связанное
покрытие их объединения, состоящее из непересекающихся интервалов,
концами которых являются только концы исходных интервалов:![[x_{jk} ,x_{jk}^\prime ],\quad \quad j = 1,\ldots ,n,\quad k = 1,\ldots ,m_j
- 1.](/sites/default/files/tex_cache/4e70ee3a5df7315d07a19aaf61559936.png)
- Образуем на основе полученных покрытий непересекающиеся
гиперпараллелепипеды:
![T_k = [x_{ik} ,x_{ik}^\prime ] \times \ldots \times [x_{nk} ,x_{nk}^\prime
],\quad \quad k = 1,\ldots ,m'.](/sites/default/files/tex_cache/e2618eb80d50946c24a0b42a807d539e.png)
- Вычисляем для
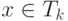 .
.
- Полагаем номер итерации
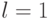 .
. - Вводим коэффициенты компетентности
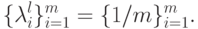
- Вычисляем приближение функции принадлежности при
нормированных
 , т.е.
, т.е.  :
: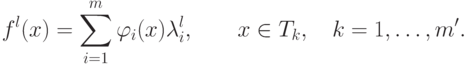
- Вычисляем функционал рассогласования мнения
 -го
эксперта с мнением
экспертного совета на
-го
эксперта с мнением
экспертного совета на  -й итерации:
-й итерации:![\delta _i^l = \sum\limits_{\begin{subarray}{c}
{x \in T_k } \\
{k = 1,\ldots ,m'} \\
\end{subarray} } {[f^l (x) - \varphi _i (x)]^2 } ,\quad \quad i = 1,\ldots ,m.](/sites/default/files/tex_cache/5a5906cefc257fc0d87962833d7fcba0.png)
- Вычисляем
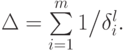
- Присваиваем
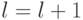 .
. - Вычисляем
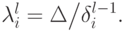
- Если величина
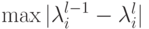 близка к нулю, то вычисления прекращаем и приближением функции принадлежности
считаем
близка к нулю, то вычисления прекращаем и приближением функции принадлежности
считаем  , в противном случае возвращаемся к шагу
6.
, в противном случае возвращаемся к шагу
6.
Опишем кратко косвенный метод, предложенный
З.А.Киквидзе.
Пусть  — универсальное множество,
— универсальное множество,  —
понятие, общее название элементов.
Задача определения нечеткого подмножества
—
понятие, общее название элементов.
Задача определения нечеткого подмножества  , описывающего понятие
, описывающего понятие  ,
решается путем опроса экспертов. Каждый эксперт
,
решается путем опроса экспертов. Каждый эксперт 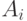 (
( 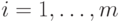 ) выделяет
из
) выделяет
из  множество элементов
множество элементов 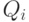 , по его мнению,
соответствующих понятию
, по его мнению,
соответствующих понятию  .
Ранжируя все элементы множества
.
Ранжируя все элементы множества 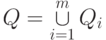 по
предпочтению в смысле соответствия понятию
по
предпочтению в смысле соответствия понятию  , каждый эксперт
упорядочивает
, каждый эксперт
упорядочивает  ,
используя отношение порядка
,
используя отношение порядка 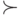 или
или  .
Отношение
.
Отношение  указывает
на одинаковую степень предпочтения между любыми элементами
указывает
на одинаковую степень предпочтения между любыми элементами  .
Предполагается, что эксперты могут поставить коэффициенты степени предпочтения
.
Предполагается, что эксперты могут поставить коэффициенты степени предпочтения  перед элементами в упорядоченной последовательности, усиливая или ослабляя
отношение
предпочтения. Вводится расстояние между элементами указанной
последовательности
перед элементами в упорядоченной последовательности, усиливая или ослабляя
отношение
предпочтения. Вводится расстояние между элементами указанной
последовательности 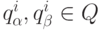 :
:

Здесь  ,
,  — порядковые номера
элементов в упорядочении.
Расстояние вычисляется через первый в упорядочении элемент:
— порядковые номера
элементов в упорядочении.
Расстояние вычисляется через первый в упорядочении элемент:

Эта разность показывает, насколько предпочтительнее 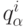 по сравнению с
по сравнению с 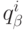 .
При решении задачи взвешивания предпочтительности элементов множества
.
При решении задачи взвешивания предпочтительности элементов множества  предполагается, что разность между весами
предполагается, что разность между весами 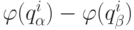 пропорциональна разности
пропорциональна разности 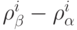 :
: 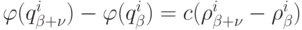 .
Когда
.
Когда  , формула превращается в рекуррентную формулу, и
задача сводится к определению
веса первого элемента. При использовании рекуррентных формул вес последнего
элемента
должен отличаться от нуля. Например, в качестве
, формула превращается в рекуррентную формулу, и
задача сводится к определению
веса первого элемента. При использовании рекуррентных формул вес последнего
элемента
должен отличаться от нуля. Например, в качестве  можно
выбрать
можно
выбрать 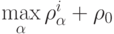 . На основании
всех
. На основании
всех  для
для  определяется
значение
определяется
значение 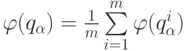 ;
это и есть степень принадлежности элемента
;
это и есть степень принадлежности элемента  некоторому
нечеткому
множеству с общим названием
некоторому
нечеткому
множеству с общим названием  .
.
Зиммерман предлагает метод, сочетающий преимущества косвенных методов в их
простоте и стойкости к искажениям ответов экспертов и преимущества прямых методов,
позволяющих получить непосредственно значения степени принадлежности.
Выборку объектов необходимо проводить так, чтобы достаточно равномерно
представить степень принадлежности от  до
до  по
отношению к рассматриваемому
нечеткому множеству. Эта выборка должна удовлетворять условию безоговорочного
экстремума, т.е. должна содержать, по крайней мере, два объекта,
значения функции принадлежности на которых имеют определенность
по
отношению к рассматриваемому
нечеткому множеству. Эта выборка должна удовлетворять условию безоговорочного
экстремума, т.е. должна содержать, по крайней мере, два объекта,
значения функции принадлежности на которых имеют определенность  и
и  (все эксперты приписывают эти числа экстремумам). Далее, когда множество подходящих
объектов отобрано, эксперты опрашиваются о степенях принадлежности в
процентной шкале.
Оценка позиции по шкале каждого объекта определяется посредством медианы из
распределений
значений принадлежности. В качестве процедуры шкалирования используется метод,
основанный на законе Терстона об измерении категорий. Процедура, требующая
отсортировки
(все эксперты приписывают эти числа экстремумам). Далее, когда множество подходящих
объектов отобрано, эксперты опрашиваются о степенях принадлежности в
процентной шкале.
Оценка позиции по шкале каждого объекта определяется посредством медианы из
распределений
значений принадлежности. В качестве процедуры шкалирования используется метод,
основанный на законе Терстона об измерении категорий. Процедура, требующая
отсортировки  объектов в
объектов в 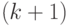 категории на
некотором континууме свойств
категории на
некотором континууме свойств  экспертами, дает распределение частоты для каждого объекта по категориям.
Средние значения границ категорий, полученные методом наименьших квадратов,
позволяют определить значения оценок объектов на шкале.
экспертами, дает распределение частоты для каждого объекта по категориям.
Средние значения границ категорий, полученные методом наименьших квадратов,
позволяют определить значения оценок объектов на шкале.

