| Казахстан, Алматы |
Арифметичность вычислимых функций
Теоремы Тарского и Геделя
Поскольку графики вычислимых функций арифметичны, очевидно, разрешимые и перечислимые множества тоже будут арифметическими. Тем самым мы можем
оправдать название " арифметическая иерархия" для классов  и
и  :
:
Теорема 68. При любом n любое множество из класса  или
или  арифметично (есть формула арифметики, выражающая
принадлежность этому множеству).
арифметично (есть формула арифметики, выражающая
принадлежность этому множеству).
После того, как мы доказали арифметичность вычислимых функций,
все ясно множества из классов  и
и  получаются навешиванием кванторов на разрешимые множества, а
разрешимое множество арифметично.
получаются навешиванием кванторов на разрешимые множества, а
разрешимое множество арифметично.
Верно и обратное:
Теорема 69. Всякое арифметическое множество лежит в классе  или
или  для некоторого n (и, естественно, для всех
больших n ).
для некоторого n (и, естественно, для всех
больших n ).
Формулу, задающую арифметическое множество, приведем к
предваренной нормальной форме (вынеся кванторы наружу).
Ясно, что бескванторная часть
задает разрешимое множество, поэтому исходное
множество принадлежит какому-то из классов  или
или  .
.
Можно и не использовать предваренной нормальной формы, а
применить индукцию по длине формулы и сослаться на то, что
пересечение, объединение и дополнение, а также проекция не
выводят за пределы арифметической иерархии (объединения всех
классов  и
и  ).
).
Рассмотрим теперь множество T, элементами которого являются все истинные арифметические формулы без параметров (точнее, их номера в какой-то вычислимой нумерации всех формул это значит, что по формуле можно алгоритмически получить ее номер и наоборот).
Теорема 70. Любое арифметическое множество m -сводится к множеству T.
Это утверждение почти очевидно. Пусть A произвольное
арифметическое множество. Пусть 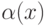 формула с одной переменной, которая выражает принадлежность множеству A. Это
означает, что
формула с одной переменной, которая выражает принадлежность множеству A. Это
означает, что 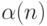 истинно при тех и только
тех n,
которые принадлежат A. Тогда
вычислимая
функция n
истинно при тех и только
тех n,
которые принадлежат A. Тогда
вычислимая
функция n  номер
формулы, которая является результатом подстановки
константы n в
номер
формулы, которая является результатом подстановки
константы n в 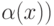 m -сводит A к T.
m -сводит A к T.
Теорема 71. Множество T не арифметично.
После проведенной нами подготовки это утверждение очевидно: если
бы T было арифметическим, то оно лежало бы в некотором
конкретном классе  . Поскольку всякое арифметическое
множество сводится к T, то по
теореме 53 все
арифметические
множества лежали бы в этом классе. Но мы знаем, что множества из
более высоких классов иерархии тоже арифметичны, но в
. Поскольку всякое арифметическое
множество сводится к T, то по
теореме 53 все
арифметические
множества лежали бы в этом классе. Но мы знаем, что множества из
более высоких классов иерархии тоже арифметичны, но в  не лежат.
не лежат.
Эта теорема называется теоремой Тарского. Ее можно прочесть так: множество арифметических истин не арифметично. Или: понятие арифметической истины невыразимо в арифметике.
Теорема 72. Множество T арифметических истин неперечислимо.
В самом деле, любое перечислимое множество арифметично.
Это утверждение называется теоремой Геделя о неполноте. Его можно переформулировать так: всякое исчисление, порождающее формулы арифметики (е алгоритм, перечисляющий некоторое множество таких формул) либо неадекватно (порождает некоторую ложную формулу), либо неполно (не порождает некоторой истинной формулы).
85. Покажите, что для любого N множество всех истинных замкнутых арифметических формул, содержащих не более N кванторов, арифметично.
86. Сформулируйте и докажите аналогичное утверждения для формул ограниченной кванторной глубины (число вложенных кванторов) и для формул с ограниченным числом перемен кванторов в предваренной нормальной форме.
Прямое доказательство теорем Тарского и Геделя
В нашем изложении теоремы Тарского и Геделя получились как простые следствия определений и фактов, связанных с теорией алгоритмов. С одной стороны, это позволяет лучше понять место этих теорем в общем контексте математической логики и теории алгоритмов. С другой стороны, возникает естественное желание развернуть цепочку и получить более прямые доказательства. Таковые мы сейчас и приведем.
Начиная доказывать теорему Тарского, предположим, что множество
номеров всех истинных арифметических формул (без параметров)
арифметично. Пусть T это множество, а 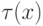 соответствующая формула. Перенумеруем также все формулы с одним
параметром x ; пусть Fn(x) формула, имеющая
номер n в
этой нумерации. Рассмотрим формулу с единственным
параметром x, утверждающую, что результат подстановки
константы x в x -ую формулу с параметром ложен. Эту формулу можно написать
так:
соответствующая формула. Перенумеруем также все формулы с одним
параметром x ; пусть Fn(x) формула, имеющая
номер n в
этой нумерации. Рассмотрим формулу с единственным
параметром x, утверждающую, что результат подстановки
константы x в x -ую формулу с параметром ложен. Эту формулу можно написать
так:

где Subst(p,q,r) формула с тремя параметрами, выражающая такое свойство: " p есть номер (в нумерации всех формул без параметров) той формулы, которая получится, если в q -ю формулу с одним параметром подставить константу r вместо этого параметра". Записанное в кавычках свойство описывает график некоторой вычислимой функции (соответствующей простым синтаксическим действиям и переходу от одной нумерации к другой) и потому существует выражающая его формула.
Итак, мы написали некоторую формулу с единственным параметром x. Пусть она имеет некоторый номер N. Подставим этот номер N вместо ее параметра. Получится некоторая формула без параметров. Из построения видно, что эта формула истинна тогда и только тогда, когда результат подстановки числа N в формулу номер N (то есть сама эта формула!) ложен.
Полученное противоречие завершает прямое доказательство теоремы Тарского. Мы видим, что нам потребовалась выразимость в арифметике не любых вычислимых функций, а одной вполне конкретной. При достаточном терпении соответствующую формулу можно-таки написать, и тем самым доказательство станет совсем " осязаемым".
Теперь изложим в том же стиле доказательство теоремы Геделя. Как мы уже говорили, исчисление это механизм (алгоритм), который позволяет порождать некоторые формулы языка арифметики (для простоты будем считать, что порождаются только формулы без параметров). Таким образом, возникает некоторое перечислимое множество, которое обычно задают как проекцию разрешимого множества. Именно, вводят некоторое понятие доказательства. При этом доказательства являются словами в некотором алфавите. Множество доказательств разрешимо, то есть есть алгоритм, отличающий настоящие доказательства от текстов, который таковыми не являются. Кроме того, есть (также разрешимое) свойство двух слов x и y, которое гласит, что x есть доказательство формулы y. Перенумеровав все доказательства и формулы и выразив указанные разрешимые свойства в языке арифметики, мы приходим к формуле Proof(x,y), которая истинна, когда x есть номер доказательства формулы с номером y.
Теперь напишем формулу с одним параметром x, которая говорит, что результат подстановки числа x вместо параметра в x -ую формулу с одним параметром не имеет доказательства:
![\neg \exists\ z\ \exists\ p\ [Subst(z,x,x) \wedge Proof(p,z)]](/sites/default/files/tex_cache/97429aa35f2fed641c9d03baab803835.png)
Эта формула имеет единственный параметр ( x ); пусть ее номер в
нумерации таких формул равен N. Подставим N вместо
параметра. Получится формула без параметров 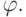 По
построению формула
По
построению формула  истинна, когда результат
подстановки N в N -ю формулу с одним параметром
недоказуем. А
этот результат есть сама формула
истинна, когда результат
подстановки N в N -ю формулу с одним параметром
недоказуем. А
этот результат есть сама формула  так что она истинна
тогда и только тогда, когда недоказуема. Значит, наше исчисление
либо позволяет доказать ложную формулу
так что она истинна
тогда и только тогда, когда недоказуема. Значит, наше исчисление
либо позволяет доказать ложную формулу  (если
(если  ложна;
в таком случае его называют неадекватным), либо не
позволяет доказать истинную формулу
ложна;
в таком случае его называют неадекватным), либо не
позволяет доказать истинную формулу 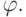
Заметим, что оба этих доказательства напоминают как построение неподвижной точки, так и классический парадокс лжеца: