Информационные технологии
Оптимальное кодирование, свойства оптимальных кодов, построение оптимальных кодов методом Хафмена
Для практических целей представляет интерес нахождение для каждого источника префиксного кода с минимальной средней длиной кодирования.
Определение. Префиксное кодирование 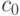 называется оптимальным для источника
называется оптимальным для источника  , если для каждого префиксного кодирования c источника
, если для каждого префиксного кодирования c источника  справедливо неравенство
справедливо неравенство  .
.
Для каждого источника существует оптимальный код, поскольку множество префиксных кодов источника с избыточностью, меньшей либо равной 1, не пусто и конечно. Один источник может иметь несколько оптимальных кодов с разными наборами длин кодовых слов.
Пусть буквы алфавита 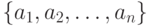 источника
источника  имеют вероятности появления
имеют вероятности появления 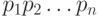 , длины кодовых слов
, длины кодовых слов 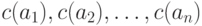 при использовании кода
при использовании кода  равны
равны 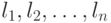 . Рассмотрим некоторые свойства оптимального кодирования, для того чтобы, опираясь на эти свойства, сформулировать процедуру нахождения оптимального кода.
. Рассмотрим некоторые свойства оптимального кодирования, для того чтобы, опираясь на эти свойства, сформулировать процедуру нахождения оптимального кода.
Свойство 1. Для оптимального кода из  следует, что
следует, что  .
.
Для доказательства предположим противное, т. е. что для оптимального кода существуют 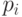 и
и 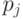 , такие что
, такие что  и
и  . Построим новый код, поменяв местами кодовые слова рассматриваемого оптимального кода для
. Построим новый код, поменяв местами кодовые слова рассматриваемого оптимального кода для  -ой и
-ой и  -ой букв алфавита. Разность между средней длиной
-ой букв алфавита. Разность между средней длиной 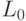 кодирования оптимальным кодом и средний длиной
кодирования оптимальным кодом и средний длиной  построенного кода имеет вид
построенного кода имеет вид
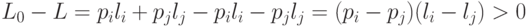
что противоречит оптимальности рассматриваемого кода.
Свойство 2. Существует оптимальный код источника  , для которого
, для которого

причем два последних слова имеют максимальную длину и отличаются только в последнем знаке.
Предположим, что в оптимальном коде не существует двух слов максимальной длины. Это значит, существует только одно слово максимальной длины. Если это самое длинное слово сократить на один последний знак, а другие кодовые слова оставить неизменными, то получится новый код, который, во-первых, будет префиксным (нет второго слова, которое отличается в последнем знаке), и, во-вторых, средняя длина кодирования будет меньше. Это противоречит предположению о существовании в оптимальном коде только одного слова максимальной длины. Таким образом, в оптимальном коде существует, по крайней мере, два кодовых слова максимальной длины.
Докажем, что какие-то два слова максимальной длины отличаются только в последнем знаке. Опять предположим противное, то есть любые два слова максимальной длины отличаются не только в последнем знаке. В этой ситуации можно повторить описанную выше процедуру укорачивания одного из слов максимальной длины и получить в результате новый префиксный код с меньшей средней длиной кодирования, что противоречит оптимальности исходного кода.
Опираясь на рассмотренные свойства, можно построить оптимальный для заданного источника  код с использованием двух процедур: сжатия источника и расщепления кода. Смысл первой процедуры заключается в том, что исходный источник последовательно заменяется на более простой (содержащий на 1 меньше знаков) источник. Применение процедуры сжатия заканчивается, когда будет получен простейший источник с двумя знаками, оптимальное кодирование которого очевидно. Процедура расщепления кода предназначена для построения из оптимального кода более простого источника оптимального кода того источника, из которого процедурой сжатия был получен простой источник.
код с использованием двух процедур: сжатия источника и расщепления кода. Смысл первой процедуры заключается в том, что исходный источник последовательно заменяется на более простой (содержащий на 1 меньше знаков) источник. Применение процедуры сжатия заканчивается, когда будет получен простейший источник с двумя знаками, оптимальное кодирование которого очевидно. Процедура расщепления кода предназначена для построения из оптимального кода более простого источника оптимального кода того источника, из которого процедурой сжатия был получен простой источник.
Процедура сжатия источника заключается в переходе от источника  с алфавитом из n знаков
с алфавитом из n знаков 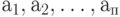 упорядоченных в порядке невозрастания соответствующих им вероятностей
упорядоченных в порядке невозрастания соответствующих им вероятностей 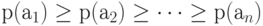 , к источнику
, к источнику 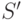 с алфавитом из
с алфавитом из  знака
знака 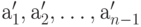 и вероятностями
и вероятностями  при
при 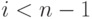 и
и 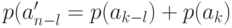 .
.
Операцию сжатия источника  будем обозначать через
будем обозначать через 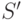 Фактически, при сжатии первые
Фактически, при сжатии первые  знака остаются неизменными, а два последних, наименее вероятных знака заменяются на некоторый новый знак с вероятностью, равной сумме вероятностей двух заменяемых знаков.
знака остаются неизменными, а два последних, наименее вероятных знака заменяются на некоторый новый знак с вероятностью, равной сумме вероятностей двух заменяемых знаков.

Применяя сжатие к источнику  , получим новый источник
, получим новый источник  , применяя затем процедуру сжатия к
, применяя затем процедуру сжатия к 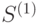 получим
получим 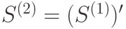 . Действуя подобным образом
. Действуя подобным образом  раза, построим последовательность источников
раза, построим последовательность источников  ,
,  .
.
Алфавит источника 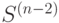 состоит только из двух знаков, поэтому найти оптимальный код для этого источника не составляет труда. Одно из слов кодируется знаком 0, а другое - знаком 1. Это особенно важно потому, что, используя оптимальный код для источника
состоит только из двух знаков, поэтому найти оптимальный код для этого источника не составляет труда. Одно из слов кодируется знаком 0, а другое - знаком 1. Это особенно важно потому, что, используя оптимальный код для источника 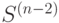 и последовательность кодов
и последовательность кодов  , можно найти оптимальный код для исходного источника
, можно найти оптимальный код для исходного источника  .
.
Для построения оптимального кода источника  , содержащего на один знак больше, чем источник
, содержащего на один знак больше, чем источник  , необходимо выполнить процедуру расщепления кода.
, необходимо выполнить процедуру расщепления кода.
Пусть имеем источник
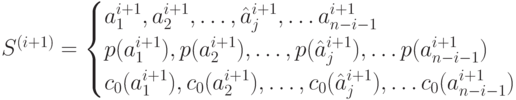
И оптимальный код 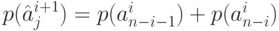
Через 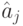 обозначен тот знак алфавита источника
обозначен тот знак алфавита источника  , который заменил два знака с минимальными вероятностями источника
, который заменил два знака с минимальными вероятностями источника  при его сжатии.
при его сжатии.
Процедура расщепления заключается в использовании оптимального кода 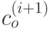 источника
источника  для построения оптимального кода для источника
для построения оптимального кода для источника  . Она заключается в следующем: знакам алфавита источника
. Она заключается в следующем: знакам алфавита источника  , перешедшим в
, перешедшим в  без изменения, назначаются кодовые слова совпадающих с ними знаков источника
без изменения, назначаются кодовые слова совпадающих с ними знаков источника  ; двум наименее вероятным знакам алфавита источника
; двум наименее вероятным знакам алфавита источника  , замененным в процессе сжатия на знак
, замененным в процессе сжатия на знак 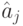 , сопоставляют кодовые слова
, сопоставляют кодовые слова 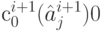 и
и 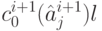 .
.
Слово 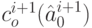 в оптимальном коде источника
в оптимальном коде источника  , содержащем
, содержащем 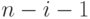 знаков, "расщепляется", путем добавления (конкатенации) знаков 0 и 1, на 2 слова в кодовом множестве для источника
знаков, "расщепляется", путем добавления (конкатенации) знаков 0 и 1, на 2 слова в кодовом множестве для источника  , содержащем
, содержащем 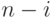 знаков.
знаков.
Средняя длина 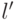 кода источника
кода источника  и средняя длина
и средняя длина  кода, полученного из него расщеплением, связаны соотношением
кода, полученного из него расщеплением, связаны соотношением 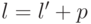 . Действительно,
. Действительно,
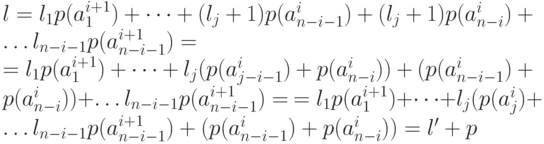
Докажем, что получающийся в результате расщепления код является оптимальным для источника  .
.
Предположим противное, т. е. что существует другой оптимальный код 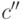 для того же источника
для того же источника  со средней длиной кодирования
со средней длиной кодирования 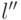 , меньшей, чем
, меньшей, чем  , т. е.
, т. е. 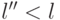 . В соответствии со свойством 2 оптимальный код содержит два слова максимальной длины, отличающиеся в последнем знаке и соответствующие двум наименьшим вероятностям источника
. В соответствии со свойством 2 оптимальный код содержит два слова максимальной длины, отличающиеся в последнем знаке и соответствующие двум наименьшим вероятностям источника  . Обозначим эти два слова через
. Обозначим эти два слова через  и
и  . Из этого кода для источника
. Из этого кода для источника  можно построить код
можно построить код 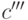 для источника
для источника  , в котором последнее кодовое слово получается отбрасыванием последнего знаки из слов
, в котором последнее кодовое слово получается отбрасыванием последнего знаки из слов  и
и  . Средняя длина
. Средняя длина 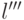 кода
кода 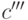 связана со средней длиной
связана со средней длиной 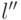 кода
кода 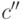 соотношением
соотношением 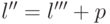 . Из этого соотношения, из соотношения
. Из этого соотношения, из соотношения 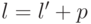 и из предположения, что
и из предположения, что 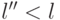 , следует, что
, следует, что  . Это противоречит оптимальности кода для источника
. Это противоречит оптимальности кода для источника  .
.
Таким образом, используя процедуру расщепления, строится оптимальный код для источника, который ранее был преобразован процедурой сжатия в более простой источник. Повторяя эту процедуру необходимое количество раз, можно будет найти оптимальный код для исходного источника  .
.
Описанный метод оптимального кодирования был предложен в 1952 г. Д. Хафменом и называется его именем. В общем случае, когда для кодирования используется алфавит из более чем двух букв, метод Хафмена рассмотрен в [32].
Рассмотрим процесс построения оптимального кода на примере источника из пяти сообщений с вероятностями 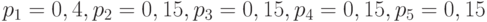 . Построение кода показано на следующем рисунке.
. Построение кода показано на следующем рисунке.
Стрелками показаны шаги сжатия источника. В левой части каждого столбца показано распределение вероятностей источника. В правой части каждого столбца, соответствующего одному из источников, показаны кодовые слова. Построение кода начинается с простейшего источника 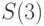 , который кодируется двумя однобуквенными словами 0 и 1.
, который кодируется двумя однобуквенными словами 0 и 1.
В данном случае средняя длина кодирования для оптимального кода, построенного методом Хафмена, составляет 2,2. Это меньше, чем средняя длина кода, построенного ранее методом Фано для того же источника.


