Криптографические алгоритмы с открытым ключом и их использование

Пример вычислений по алгоритму

Пусть два абонента, желающие обмениваться через Интернет зашифрованными сообщениями, решили сформировать секретный ключ для очередного сеанса связи. Пусть они имеют следующие общие параметры:

Р = 11, А = 7.

Каждый абонент выбирает секретное число Х и вычисляет соответствующее ему открытое число Y. Пусть выбраны

Х1 = 3, Х2= 9.

Вычисляем

Y1 = 73 mod 11 = 2,
Y2= 79 mod 11 = 8.

Затем пользователи обмениваются открытыми ключами Y₁ и Y₂. После этого каждый из пользователей может вычислить общий секретный ключ:

пользователь 1: Z = 83 mod 11 = 6.
пользователь 2: Z = 29 mod 11 = 6.

Теперь они имеют общий ключ 6, который не передавался по каналу связи.

Вопросы практического использования алгоритма Диффи-Хеллмана

Для того, чтобы алгоритм Диффи-Хеллмана работал правильно, то есть оба пользователя, участвующих в протоколе, получали одно и то же число Z, необходимо правильным образом выбрать число А, используемое в вычислениях. Число А должно обладать следующим свойством: все числа вида

A mod P, A2 mod P, A3 mod P,... , AP-1 mod P

должны быть различными и состоять из целых положительных значений в диапазоне от 1 до Р-1 с некоторыми перестановками. Только в этом случае для любого целого Y < Р и значения A можно найти единственную экспоненту Х, такую, что

Y = AХmod P, где 0 <= X <= (P - 1)

При произвольно заданном Р задача выбора параметра А может оказаться трудной задачей, связанной с разложением на простые множители числа Р-1. На практике можно использовать следующий подход, рекомендуемый специалистами. Простое число Р выбирается таким, чтобы выполнялось равенство Р = 2q + l, где q — также простое число. Тогда в качестве А можно взять любое число, для которого справедливы неравенства

1<A<P-1    и    Aq mod P ≠ 1

На подбор подходящих параметров А и Р необходимо некоторое время, однако это обычно не критично для системы связи и не замедляет ее работу. Эти параметры являются общими для целой группы пользователей. Они обычно выбираются один раз при создании сообщества пользователей, желающих использовать протокол Диффи-Хеллмана, и не меняются в процессе работы. А вот значения закрытых ключей рекомендуется каждый раз менять и выбирать их с помощью генераторов псевдослучайных чисел.

Следует заметить, что данный алгоритм, как и все алгоритмы асимметричного шифрования, уязвим для атак типа "man-in-the-middle" ("человек в середине"). Если противник имеет возможность не только перехватывать сообщения, но и заменять их другими, он может перехватить открытые ключи участников, создать свою пару открытого и закрытого ключа и послать каждому из участников свой открытый ключ. После этого каждый участник вычислит ключ, который будет общим с противником, а не с другим участником. Способы предотвращения такой атаки и некоторых других рассмотрены в конце этой лекции.

Алгоритм Эль-Гамаля

Основные сведения

Асимметричный алгоритм, предложенный в 1985 году Эль-Гамалем (T. ElGamal), универсален. Он может быть использован для решения всех трех основных задач: для шифрования данных, для формирования цифровой подписи и для согласования общего ключа. Кроме того, возможны модификации алгоритма для схем проверки пароля, доказательства идентичности сообщения и другие варианты. Безопасность этого алгоритма, так же как и алгоритма Диффи-Хеллмана, основана на трудности вычисления дискретных логарифмов. Этот алгоритм фактически использует схему Диффи-Хеллмана, чтобы сформировать общий секретный ключ для абонентов, передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ.

И в случае шифрования, и в случае формирования цифровой подписи каждому пользователю необходимо сгенерировать пару ключей. Для этого, так же как и в схеме Диффи-Хеллмана, выбираются некоторое большое простое число Р и число А, такие, что различные степени А представляют собой различные числа по модулю Р. Числа Р и А могут передаваться в открытом виде и быть общими для всех абонентов сети.

Затем каждый абонент группы выбирает свое секретное число Х_i, 1 < Х_i < Р-1, и вычисляет соответствующее ему открытое число . Таким образом, каждый пользователь может сгенерировать закрытый ключ Х_i и открытый ключ Y_i.

Информация о необходимых параметрах системы сведена в следующую таблицу.

Шифрование

Теперь рассмотрим, каким образом производится шифрование данных. Сообщение, предназначенное для шифрования, должно быть представлено в виде одного числа или набора чисел, каждое из которых меньше Р. Пусть пользователь 1 хочет передать пользователю 2 сообщение m. В этом случае последовательность действий следующая.

1. Первый пользователь выбирает случайное число k, взаимно простое с Р-1, и вычисляет числа
   
   где Y₂ – открытый ключ пользователя 2. Число k держится в секрете.
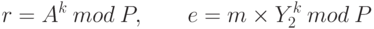
2. Пара чисел (r, е), являющаяся шифротекстом, передается второму пользователю.
3. Второй пользователь, получив (r,e), для расшифрования сообщения вычисляет
   
   где Х₂ – закрытый ключ пользователя 2. В результате он получает исходное сообщение m.

Если злоумышленник узнает или перехватит Р, А, Y₂, r, e, то он не сможет по ним раскрыть m. Это связано с тем, что противник не знает параметр k, выбранный первым пользователем для шифрования сообщения m. Вычислить каким-либо образом число k практически невозможно, так как это задача дискретного логарифмирования. Следовательно, злоумышленник не может вычислить и значение m, так как m было умножено на неизвестное ему число. Противник также не может воспроизвести действия законного получателя сообщения (второго абонента), так как ему не известен закрытый ключ Х₂ (вычисление Х₂ на основании Y₂ — также задача дискретного логарифмирования).

По аналогичному алгоритму может производиться и согласование ключа, используемого для симметричного шифрования больших объемов данных. Более того, алгоритм Эль-Гамаля на практике целесообразно использовать именно для согласования общего ключа сессии, а не прямого шифрования больших сообщений. Это связано с тем, что в алгоритме используются операции возведения в степень и умножения по большому модулю. Так же как и в алгоритмах RSA и Диффи-Хеллмана, операции производятся над большими, состоящими из нескольких сотен или тысяч бит, числами. Поэтому шифрование больших сообщений производится крайне медленно.