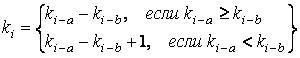Поточные шифры и генераторы псевдослучайных чисел. Часть 1

Линейный конгруэнтный генератор псевдослучайных чисел

Генераторы псевдослучайных чисел могут работать по разным алгоритмам. Одним из простейших генераторов является так называемый линейный конгруэнтный генератор, который для вычисления очередного числа k_i использует формулу

ki=(a*ki-1+b)mod c,

где а, b, с — некоторые константы, a k_i-1 — предыдущее псевдослучайное число. Для получения k₁ задается начальное значение k₀. Возьмем в качестве примера a=5,b=3,c=11 и пусть k₀= 1. В этом случае мы сможем по приведенной выше формуле получать значения от 0 до 10 (так как с = 11). Вычислим несколько элементов последовательности:

k1 = (5 * 1 + 3) mod 11 = 8;
k2 = (5 * 8 + 3) mod 11 = 10;
k3 = (5 * 10 + 3) mod 11 = 9;
k4 = (5 * 9 + 3) mod 11 = 4;
k5 = (5 * 4 + 3) mod 11 = 1.

Полученные значения (8, 10, 9, 4, 1) выглядят похожими на случайные числа. Однако следующее значение k₆ будет снова равно 8:

k6 = (5 * 1 + 3) mod 11 = 8,

а значения k₇ и k₈ будут равны 10 и 9 соответственно:

k7 = (5 * 8 + 3) mod 11 = 10;
k8= (5 * 10 + 3) mod 11 = 9.

Выходит, наш генератор псевдослучайных чисел повторяется, порождая периодически числа 8, 10, 9, 4, 1. К сожалению, это свойство характерно для всех линейных конгруэнтных генераторов. Изменяя значения основных параметров a, b и c, можно влиять на длину периода и на сами порождаемые значения k_i. Так, например, увеличение числа с в общем случае ведет к увеличению периода. Если параметры a, b и c выбраны правильно, то генератор будет порождать случайные числа с максимальным периодом, равным c. При программной реализации значение с обычно устанавливается равным 2^b-1 или 2^b, где b — длина слова ЭВМ в битах.

Достоинством линейных конгруэнтных генераторов псевдослучайных чисел является их простота и высокая скорость получения псевдослучайных значений. Линейные конгруэнтные генераторы находят применение при решении задач моделирования и математической статистики, однако в криптографических целях их нельзя рекомендовать к использованию, так как специалисты по криптоанализу научились восстанавливать всю последовательность ПСЧ по нескольким значениям. Например, предположим, что противник может определить значения k₀, k₁, k₂, k₃. Тогда:

k1=(a*k0+b) mod c
k2=(a*k1+b) mod c
k3=(a*k2+b) mod c

Решив систему из этих трех уравнений, можно найти a, b и c.

Для получения псевдослучайных чисел предлагалось использовать также квадратичные и кубические генераторы:

ki=(a12*ki-1+a2*ki-1+b) mod c
ki=(a13*ki-1+a22*ki-1+a3*ki-1+b) mod c

Однако такие генераторы тоже оказались непригодными для целей криптографии по той же самой причине "предсказуемости".

Метод Фибоначчи с запаздыванием

Известны и другие схемы получения псевдослучайных чисел.

Метод Фибоначчи с запаздываниями (Lagged Fibonacci Generator) — один из методов генерации псевдослучайных чисел. Он позволяет получить более высокое "качество" псевдослучайных чисел.

Наибольшую популярность фибоначчиевы датчики получили в связи с тем, что скорость выполнения арифметических операций с вещественными числами сравнялась со скоростью целочисленной арифметики, а фибоначчиевы датчики естественно реализуются в вещественной арифметике.

Известны разные схемы использования метода Фибоначчи с запаздыванием. Один из широко распространённых фибоначчиевых датчиков основан на следующей рекуррентной формуле:

где k_i — вещественные числа из диапазона [0,1], a, b — целые положительные числа, параметры генератора. Для работы фибоначчиеву датчику требуется знать max{a,b} предыдущих сгенерированных случайных чисел. При программной реализации для хранения сгенерированных случайных чисел необходим некоторый объем памяти, зависящих от параметров a и b.

Пример. Вычислим последовательность из первых десяти чисел, генерируемую методом Фибоначчи с запаздыванием начиная с k₅ при следующих исходных данных: a = 4, b = 1, k₀=0.1; k₁=0.7; k₂=0.3; k₃=0.9; k₄=0.5:

k5 = k1 - k4 = 0.7 - 0.5 = 0.2;
k6 = k2 - k5= 0.3 - 0.2 = 0.1;
k7 = k3 - k6 = 0.9 - 0.1 = 0.8;
k8 = k4 - k7 + 1 =0.5 - 0.8 + 1 = 0.7;
k9 = k5- k8 + 1 =0.2 - 0.7 + 1 = 0.5;
k10 = k6 - k9 + 1 =0.1 - 0.5 + 1 = 0.6;
k11 = k7 - k10 = 0.8 - 0.6 = 0.2;
k12 = k8 - k11 = 0.7 - 0.2 = 0.5;
k13 = k9 - k12 + 1 =0.5 - 0.5 + 1 = 1;
k14 = k10 - k13 + 1 =0.6 - 1 + 1 = 0.6.

Видим, что генерируемая последовательность чисел внешне похожа на случайную. И действительно, исследования подтверждают, что получаемые случайные числа обладают хорошими статистическими свойствами.

Для генераторов, построенных по методу Фибоначчи с запаздыванием, существуют рекомендуемые параметры a и b, так сказать, протестированные на качество. Например, исследователи предлагают следующие значения: (a,b) = (55, 24), (17, 5) или (97,33). Качество получаемых случайных чисел зависит от значения константы a: чем оно больше, тем выше размерность пространства, в котором сохраняется равномерность случайных векторов, образованных из полученных случайных чисел. В то же время с увеличением величины константы a увеличивается объём используемой алгоритмом памяти.

В результате значения (a,b) = (17,5) рекомендуются для простых приложений. Значения (a,b) = (55,24) позволяют получать числа, удовлетворительные для большинства криптографических алгоритмов, требовательных к качеству случайных чисел. Значения (a,b) = (97,33) позволяют получать очень качественные случайные числа и используются в алгоритмах, работающих со случайными векторами высокой размерности.

Генераторы ПСЧ, основанные на методе Фибоначчи с запаздыванием, использовались для целей криптографии. Кроме того, они применяются в математических и статистических расчетах, а также при моделировании случайных процессов. Генератор ПСЧ, построенный на основе метода Фибоначчи с запаздыванием, использовался в широко известной системе Matlab.