|
мне задали дистанционное задание на сертификат,но я не могу его найти |
Базовые идеи и методы теории вероятностей
Производящие функции
Пусть  — целочисленная случайная величина, принимающая в зависимости от случайного исхода
— целочисленная случайная величина, принимающая в зависимости от случайного исхода  одно из значений 0, 1, 2, … с соответствующими вероятностями
одно из значений 0, 1, 2, … с соответствующими вероятностями
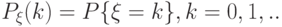 .
.
 |
( 3.13) |
называется производящей функцией случайной величины  или соответствующего распределения вероятностей
или соответствующего распределения вероятностей  .
.
 является аналитической функцией от
является аналитической функцией от  и (3.13.) дает ее разложение в степенной ряд. Ясно, что распределение вероятностей случайной величины
и (3.13.) дает ее разложение в степенной ряд. Ясно, что распределение вероятностей случайной величины  однозначно определяется ее производящей функцией
однозначно определяется ее производящей функцией  ; в частности, по формуле Тейлора
; в частности, по формуле Тейлора
 .
.
Производящая функция  при фиксированном
при фиксированном  представляет собой не что иное, как математическое ожидание случайной величины
представляет собой не что иное, как математическое ожидание случайной величины 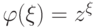 :
:
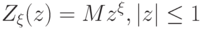 .
.
Цепи Маркова
Условно будем говорить о некоторой физической системе, шаг за шагом меняющей свое фазовое состояние. Будем считать, что имеется лишь конечное или счетное число различных фазовых состояний 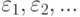 . Обозначим
. Обозначим 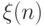 состояние системы через
состояние системы через  шагов. Будем предполагать, что цепочка последовательных переходов
шагов. Будем предполагать, что цепочка последовательных переходов
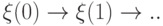 .
.
Зависит от вмешательства случая, причем соблюдается следующая закономерность: если на каком-либо шаге  система находится в состоянии
система находится в состоянии 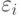 , то, независимо от предшествующих обстоятельств, она на следующем шаге с вероятностью
, то, независимо от предшествующих обстоятельств, она на следующем шаге с вероятностью 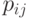 переходит в состояние
переходит в состояние 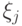 .
.
 |
( 3.14) |
Описанная выше модель называется однородной цепью Маркова , а вероятности 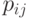 называются переходными вероятностями этой цепи. Кроме них, еще задается начальное распределение вероятностей
называются переходными вероятностями этой цепи. Кроме них, еще задается начальное распределение вероятностей
 |
( 3.15) |
Какова вероятность того, что система через  шагов будет находиться в состоянии
шагов будет находиться в состоянии 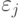 ?
?
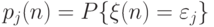 |
( 3.16) |
Через  шагов система обязательно будет находиться в одном из состояний
шагов система обязательно будет находиться в одном из состояний 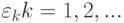 , причем в
, причем в 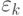 она будет с вероятностью, обозначенной
она будет с вероятностью, обозначенной  . При условии, что через
. При условии, что через 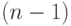 шагов система будет находиться в состоянии
шагов система будет находиться в состоянии 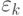 , вероятность оказаться через
, вероятность оказаться через  шагов в состоянии
шагов в состоянии 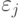 равна вероятности
равна вероятности 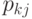 перехода из
перехода из 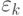 в
в 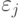 . Используя формулу полной вероятности, получим, что
. Используя формулу полной вероятности, получим, что
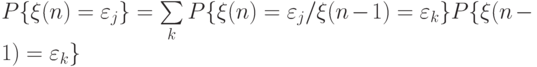 |
( 3.17) |
Это дает следующие рекуррентные соотношения для вероятностей 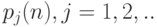 .
.
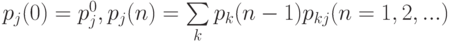 |
( 3.18) |
Если в начальный момент система находится в определенном состоянии 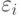 , то начальное распределение вероятностей таково, что
, то начальное распределение вероятностей таково, что 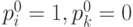 для
для  , а вероятность
, а вероятность 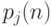 совпадает с вероятностью
совпадает с вероятностью 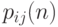 того, что система из состояния
того, что система из состояния 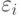 за
за  шагов перейдет в состояние
шагов перейдет в состояние 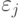 .
.
 |
( 3.19) |
При начальном распределении вида 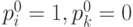 для
для  формула 3.18. дает следующие соотношения между переходными вероятностями
формула 3.18. дает следующие соотношения между переходными вероятностями  .:
.:
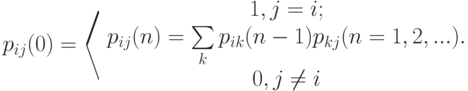 |
( 3.20) |
Удобно ввести матрицу 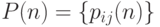 . Согласно формуле 3.20.
. Согласно формуле 3.20.
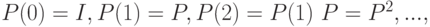 ,
,
где  — единичная матрица,
— единичная матрица, 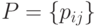 — матрица переходных вероятностей. Видно, что имеет место следующее равенство:
— матрица переходных вероятностей. Видно, что имеет место следующее равенство:
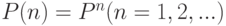 |
( 3.21) |
Случайные блуждания. Рассмотрим случайное блуждание, связанное с неограниченными испытаниями Бернулли, когда частица блуждает по целочисленным точкам действительной прямой таким образом, что, находясь в точке  , она с вероятностью p переходит на следующем шаге в соседнюю точку
, она с вероятностью p переходит на следующем шаге в соседнюю точку  , а с вероятностью
, а с вероятностью 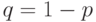 — в соседнюю точку
— в соседнюю точку 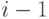 . Если обозначить
. Если обозначить 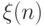 положение частицы после
положение частицы после  шагов, то последовательность
шагов, то последовательность 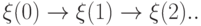 . будет цепью Маркова с переходными вероятностями вида
. будет цепью Маркова с переходными вероятностями вида
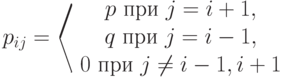 .
.
Рассмотрим случайное блуждание другого типа. Частица блуждает лишь по целым неотрицательным точкам, причем из точки  она с вероятностью
она с вероятностью 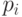 переходит на следующем шаге в соседнюю точку
переходит на следующем шаге в соседнюю точку  , а с вероятностью
, а с вероятностью 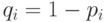 возвращается в нулевое положение. Соответствующие переходные вероятности суть
возвращается в нулевое положение. Соответствующие переходные вероятности суть
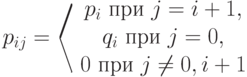 .
.
Рассмотрим цепь Маркова с состояниями 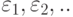 . и переходными вероятностями
. и переходными вероятностями  . Пусть в начальный момент система находится в состоянии
. Пусть в начальный момент система находится в состоянии 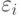 . Временно положим
. Временно положим 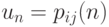 и обозначим
и обозначим 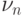 вероятность того, что через n шагов система впервые вернется в исходное состояние
вероятность того, что через n шагов система впервые вернется в исходное состояние 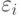 . Имеет место следующее равенство:
. Имеет место следующее равенство:
 |
( 3.22) |
где дополнительно введены 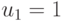 и
и 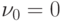 .
.
Оно является следствием общей формулы полной вероятности. Именно, если ввести события 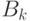 — "система через
— "система через  шагов впервые возвращается в исходное состояние
шагов впервые возвращается в исходное состояние 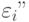 , где
, где 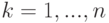 , и событие
, и событие 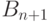 — "система ни разу не побывает в состоянии
— "система ни разу не побывает в состоянии 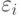 в течение первых
в течение первых  шагов", то
шагов", то 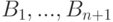 будет полной системой событий, и вероятность события
будет полной системой событий, и вероятность события  — "система через
— "система через  шагов будет находиться в исходном состоянии
шагов будет находиться в исходном состоянии 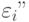 — по формуле полной вероятности есть
— по формуле полной вероятности есть
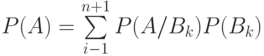 ,
,
где
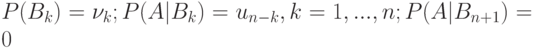 .
.
Если обратиться к производящим функциям
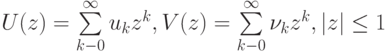
то отношение 3.22. , справедливое при всех 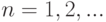 , можно написать в виде
, можно написать в виде

откуда
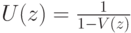 |
( 3.23) |
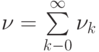 |
( 3.24) |
есть вероятность того, что система рано или поздно попадает в исходное состояние 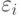 , иначе
, иначе  есть вероятность возвращения в
есть вероятность возвращения в 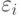 . Состояние
. Состояние 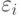 называется возвратным, если вероятность возвращения в него равна 1 , и невозвратным, если вероятность эта меньше 1.
называется возвратным, если вероятность возвращения в него равна 1 , и невозвратным, если вероятность эта меньше 1.


 , вида
, вида