НОУ ИНТУИТ | Основы информатики и программирования. Лекция 8: Проектирование цикла при помощи инварианта

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 27.09.2006 | Уровень: для всех | Доступ: платный | ВУЗ: Московский государственный индустриальный университет

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать программу

Устранение конъюнктивного члена

Этот метод хорош тем, что взяв в качестве условия продолжения цикла устраненный конъюнктивный член, мы автоматически добиваемся истинности третьего пункта теоремы 8.1., гарантирующей правильность построенного цикла.

Рассмотрим в качестве примера следующую задачу.

Задача 8.1 Напишите программу, находящую приближенное значение квадратного корня $a \in \mathbb{Z}_M^+$ из заданного неотрицательного целого числа . Вот более точная формулировка пред- и постусловия: $Q=(n\in \mathbb{Z}_M \land n \geqslant 0)$ , $R= (a \in \mathbb{Z}_M \land a \geqslant 0 \land a^2\leqslant n \land (a + 1)^2 > n)$ . При написании программы величину изменять нельзя.

Решение Построим инвариант с помощью метода устранения конъюнктивного члена (a + 1)^2 > n из постусловия: $I = (a \geqslant 0 \land a^2\leqslant n)$ . В качестве условия продолжения цикла e может быть взято отрицание удаленного конъюнктивного члена: $e=( (a + 1)^2 \leqslant n)$ , что эквивалентно выбору ограничивающей функции h=n-(a + 1)^2+1 . Истинность инварианта перед началом выполнения цикла легко устанавливается присваиванием "a=0;" и нам остается только понять, как реализовать тело цикла S.

Для того чтобы цикл завершился, величина должна увеличиваться. Простейший способ — увеличивать на единицу на каждой итерации цикла. Легко заметить, что это преобразование сохраняет инвариант, поэтому построение программы завершено. Первый вариант программы будет строго соответствовать ее спецификации.

Текст программы

public class Sqrt {
    public static void main(String[] args) throws Exception {
        int n = Xterm.inputInt("n -> ");
        int a = 0;
        while ( n >= (a+1)*(a+1) )
            a += 1;
        Xterm.println("sqrt(" + n + ") = " + a);
    }
}

Эту программу можно переписать в чуть более компактном виде:

Фрагмент программы

int a, n = Xterm.inputInt("n -> ");
        for (a=0; n >= (a+1)*(a+1); a++);
        Xterm.println("sqrt(" + n + ") = " + a);

Докажем все пять условий ее правильности.

$(Q \Rightarrow wp(S0, I)) = (n<0 \lor wp("a=0;", a \geqslant 0 \land a^2\leqslant n)) = \\ (n<0 \lor (0\geqslant 0 \land 0 \leqslant n)) = (n<0 \lor n \geqslant 0 ) = T$
$wp(S, I) = wp("a+=1;",a \geqslant 0 \land a^2\leqslant n) = \\ (a \geqslant -1 \land (a+1)^2 \leqslant n),$
поэтому $(I\land e \Rightarrow wp(S, I)) = (!I \lor !e \lor (a \geqslant -1 \land (a+1)^2 \leqslant n))$ .
Полученный предикат заведомо истинен, если ложны или , в противном случае он легко упрощается:
$wp(S, I) = (a \geqslant -1 \land (a+1)^2 \leqslant n) = (T \land T) = T$
Истинность первого конъюнктивного члена вытекает из предположения о истинности , а истинность второго — из истинности .
$(I \land !e \Rightarrow R) = (!I \lor e \lor R) = \\ (a<0 \lor a^2 >n \lor (a+1)^2 \leqslant n \lor (a \geqslant 0 \land a^2\leqslant n \land (a + 1)^2 > n)) = \\ ((a<0 \lor a^2 >n \lor (a+1)^2 \leqslant n) \lor (!(a<0 \lor a^2 >n \lor (a+1)^2 \leqslant n)) = T$
$(I \land e \Rightarrow h > 0) = (!I \lor !e \lor h >0) = (!I\lor (a+1)^2 >n \lor n-(a + 1)^2+1 >0) = \\ (!I\lor (a+1)^2 >n \lor (a + 1)^2 \leqslant n) = (!I\lor((a+1)^2 >n \lor !((a+1)^2 >n))) = (!I\lor T) = T$
$wp("h1=h; S;", h<h1) = wp("h1=n-(a+1)*(а+1)+1;",wp("a+=1;",n-(a + 1)^2+1<h1)) = \\ wp("h1=n-(a+1)*(a+1)+1;",n-(a + 2)^2+1<h1) = (n-(a + 2)^2+1<n-(a + 1)^2+1) = ((a + 1)^2<(a + 2)^2) = T$
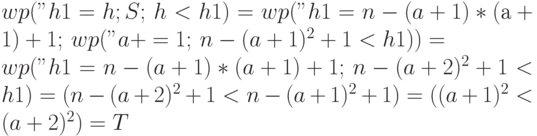
в предположении, что истинны и (так как из истинности следует $a \geqslant 0$ ).

Следовательно,

$(I\land e \Rightarrow wp("h1=h; S;", h<h1))= \\ (I\land e \Rightarrow T) = (!I \lor !e \lor T) = T.$

Применим метод устранения конъюктивного члена для построения инварианта цикла при решении еще одной задачи.

Задача 8.2 Напишите программу (линейный поиск), определяющую первое вхождение заданного целого числа в заданный массив b[0..m-1] целых чисел ( m>0 ). Известно, что находится в массиве . Значения элементов массива и число в программе изменять нельзя.

Решение Выпишем формально заданные нам пред- и постусловия: $Q = (0<m \land x \in b[0..m-1])$ , $R = ((0 \leqslant i < m) \land (\forall j\ 0 \leqslant j < i\ x \ne b[j]) \land (x = b[i]))$ .

Так как добиться истинности третьего конъюнктивного члена одним или несколькими простыми присваиваниями трудно, устраним именно его. Тогда получим $I=((0 \leqslant i < m) \land (\forall j\ 0 \leqslant j < i\ x \ne b[j]))$ . В качестве условия продолжения цикла можно взять отрицание удаленного члена ( $e=(x \ne b[i])$ ), а инвариант легко сделать истинным, выполняя команду "i=0;", поэтому программа должна иметь вид "i=0;while(x!=b[i])S;" с неизвестным нам пока S.

В качестве ограничивающей функции можно попробовать взять h=m-i , a для того, чтобы она уменьшалась, достаточно увеличивать на каждой итерации цикла. Понятно, что увеличивая более, чем на единицу, можно пропустить первое вхождение в массив, поэтому одной из команд, входящих в S, должна быть команда "i=i+1;". Так как выполнение данной команды при условии истинности сохраняет инвариант, то эта команда является единственной в теле цикла. Программа построена.

Текст программы

public class SearchL {
    static int b[], x;
    public static void main(String[] args) throws Exception {
        int m = Xterm.inputInt("m -> ");
        b = new int[m];  
        for (int k=0; k<m; k++)
            b[k] = Xterm.inputInt("b["+k+"] -> ");
        x = Xterm.inputInt("x -> ");
        int i=0;
        while (x != b[i])
            i += 1;
        Xterm.println("i = " + i);
    }
}

Докажем правильность этой программы.

$wp(S0, I) = wp("i=0;",(0 \leqslant i < m) \land (\forall j\ 0 \leqslant j < i\ x \ne b[j])) = (0<m)$ , что следует из .
$wp(S, I) = wp("i+=1;", (0 \leqslant i < m) \land (\forall j\ 0 \leqslant j < i\ x \ne b[j])) = \\ (0 \leqslant i+1 < m) \land (\forall j\ 0 \leqslant j < i+1\ x \ne b[j]),$
поэтому
$(I\land e \Rightarrow wp(S, I)) = ((((0 \leqslant i < m) \land (\forall j\ 0 \leqslant j < i\ x \ne b[j])) \land (x \ne b[i]))\\ \Rightarrow ((0 \leqslant i+1 < m) \land (\forall j\ 0 \leqslant j < i+1\ x \ne b[j]))).$
Данная импликация является тавтологией, ибо если в подмассиве элемент не встретился, то из условия задачи следует, что элемент с индексом в массиве заведомо имеется (т.е., ).
$(I \land !e \Rightarrow R) = (!(I \land !e) \lor R) = (!(I \land !e) \lor (I\land !e)) = T$
$(I \land e \Rightarrow h > 0) = (!I \lor !e \lor h >0) = \\ ((x=b[i]) \lor (i<0 \lor i\geqslant m \lor !(\forall j\ 0 \leqslant j < i\ x \ne b[j])\lor m >i)) = ((x=b[i]\lor i<0 \lor !(\forall j\ 0 \leqslant j < i\ x \ne b[j])))\lor (i<m \lor i\geqslant m) = \\ ((x=b[i]\lor i<0 \lor !(\forall j\ 0 \leqslant j < i\ x \ne b[j])))\lor T = T$
$wp("h1=h; S;", h<h1)= wp("h1=m-i;",wp("i+=1;",m-i<h1)) = \\ wp("h1=m-i;",m-i-1<h1) = (m-i-1<m-i) = T$