Все задачи курса
Задачи на предикаты
Задача 7.24. Докажите, что выражение  является предикатом.
является предикатом.
Задача 7.25. Докажите, что выражение  — не предикат.
— не предикат.
Задача 7.26. Докажите, что выражение  является предикатом.
является предикатом.
Задача 7.27. Докажите, что выражение  является предикатом.
является предикатом.
Задача 7.28. Докажите, что выражение  — не предикат.
— не предикат.
Задача 7.29. Докажите, что выражение  — не предикат.
— не предикат.
Задача 7.30. Изобразите деревья вывода для каждого из законов эквивалентности (см. "Основы языка Java" .
Задача 7.31. Вычислите значения предикатов  и
и  в состоянии
в состоянии  .
.
Задача 7.32. Вычислите значения предиката  в состоянии
в состоянии  .
.
Задача 7.33. Вычислите значения предиката  в состоянии
в состоянии 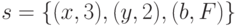 .
.
Задача 7.34. Вычислите значения предиката  в состоянии
в состоянии 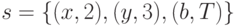 .
.
Задача 7.35. Покажите, что все законы эквивалентности (см. "Основы языка Java" ) являются тавтологиями.
Задача 7.36. Запишите предикат, утверждающий, что
если  , а
, а  , то
, то  .
.
Задача 7.37. Запишите предикат, утверждающий, что
самое большее одно из следующих утверждений истинно:  ,
,  .
.
Задача 7.38. Запишите предикат, утверждающий, что
ни одно из следующих утверждений не является истинным:  ,
,  и
и 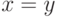 .
.
Задача 7.39. Запишите предикат, утверждающий, что
следующие утверждения не являются истинными одновременно:  ,
,  и
и 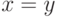 .
.
Задача 7.40. Запишите предикат, утверждающий следующее:
когда 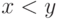 ,
,  означает, что
означает, что 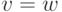 , но если
, но если  , то
, то  не может выполняться; однако если
не может выполняться; однако если 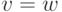 , то
, то 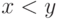 .
.
Задача 7.41. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  все элементы вырезки
все элементы вырезки ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) являются нулевыми.
являются нулевыми.
Задача 7.42. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  ни один из элементов вырезки
ни один из элементов вырезки ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) не нулевой.
не нулевой.
Задача 7.43. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  некоторые из элементов вырезки
некоторые из элементов вырезки ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) нулевые.
нулевые.
Задача 7.44. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  все нули массива находятся в вырезке
все нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 7.45. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  некоторые нули массива находятся в вырезке
некоторые нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 7.46. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
неверно, что все нули массива находятся в вырезке
справедливо высказывание:
неверно, что все нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 7.47. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
неверно, что не все нули массива находятся в вырезке
справедливо высказывание:
неверно, что не все нули массива находятся в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 7.48. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
если в
справедливо высказывание:
если в ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) есть нуль, то он есть и в вырезке
есть нуль, то он есть и в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 7.49. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
если в вырезке
справедливо высказывание:
если в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) есть два нуля, то
есть два нуля, то  .
.
Задача 7.50. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
элементы в вырезке
справедливо высказывание:
элементы в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) расположены в возрастающем порядке.
расположены в возрастающем порядке.
Задача 7.51. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
справедливо высказывание:  является степенью двойки, если
является степенью двойки, если  встречается в вырезке
встречается в вырезке ![b[j..k]](/sites/default/files/tex_cache/3b3b31473e43560c64c3e2a946b7f1b8.png) .
.
Задача 7.52. Запишите предикат, утверждающий, что
для массива ![b[0..n-1]](/sites/default/files/tex_cache/f0d2d66a2d25c9d587516c612208e85d.png) длины
длины  справедливо высказывание:
если
справедливо высказывание:
если ![b[1]](/sites/default/files/tex_cache/57a481e5acc25950be589abb7f915754.png) ,
, ![b[2]](/sites/default/files/tex_cache/b81dabf34b93c571ed2f8d564153ec91.png) и
и ![b[3]](/sites/default/files/tex_cache/9b00064932069d87bcfbb56ccf5dcead.png) есть соответственно 3, 4 и 5, то
есть соответственно 3, 4 и 5, то  .
.
Задача 7.53. Запишите предикат, который утверждает, что функция  является сюръективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
является сюръективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Задача 7.54. Запишите предикат, который утверждает, что функция  является инъективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
является инъективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Задача 7.55. Запишите предикат, который утверждает, что функция  является биективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
является биективной и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Задача 7.56. Запишите предикат, который утверждает, что функция  все элементы, не превосходящие трех, не
увеличивает, и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
все элементы, не превосходящие трех, не
увеличивает, и отрицание этого факта.
Упростите получившиеся предикаты, если это возможно.
Задача 7.57. Запишите предикат, который утверждает, что функция  все существует единственный элемент
все существует единственный элемент 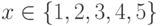 , который функция
, который функция  уменьшает, и отрицание
этого факта. Не используйте при этом квантора
уменьшает, и отрицание
этого факта. Не используйте при этом квантора  !.
!.
Задача 7.58. Основываясь на определении 6.4 и спецификации
программы 6.1, докажите истинность эквивалентности  .
.
Задача 7.59. Основываясь на определении 6.4,
докажите закон монотонности  .
.
Задача 7.60. Основываясь на определении 6.4,
докажите закон дистрибутивности дизъюнкции  .
.
Задача 7.61. Вычислите и упростите  .
.
Задача 7.62. Вычислите и упростите  .
.
Задача 7.63. Вычислите и упростите  .
.
Задача 7.64. Вычислите и упростите 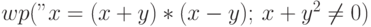 .
.
Задача 7.65. Вычислите и упростите 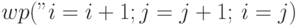 .
.
Задача 7.66. Вычислите и упростите  .
.
Задача 7.67. Вычислите и упростите ![wp("i=1; s=b[0];",
1 \leqslant i < n \ \land \ s = b[0]+\ldots+b[i-1] )](/sites/default/files/tex_cache/64aebcd8d5b6e2425396093c4594f73b.png) .
.
Задача 7.68. Вычислите и упростите  .
.
Задача 7.69. Вычислите и упростите ![wp("s=s+b[i]; i=i+1;", 0<i<n\ \land\ s=b[0]+\ldots+b[i-1])](/sites/default/files/tex_cache/549f5c9a95af97ae6f7ea9b1a07b0802.png) .
.
Задача 7.70. Вычислите и упростите  для произвольного предиката
для произвольного предиката  .
.
Задача 7.71. Вычислите и упростите следующее слабейшее предусловие  .
.
Задача 7.72. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация  становится тавтологией:
становится тавтологией: 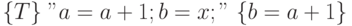 .
.
Задача 7.73. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация 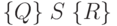 становится тавтологией:
становится тавтологией:  .
.
Задача 7.74. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация 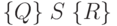 становится тавтологией:
становится тавтологией:  .
.
Задача 7.75. Найдите такое значение выражения  , включающее другие переменные,
для которого спецификация
, включающее другие переменные,
для которого спецификация 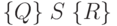 становится тавтологией:
становится тавтологией:  .
.
Задача 7.76. Задача о банке с кофейными зернами. В банке имеется несколько черных и белых кофейных зерен. Следующий процесс надо повторять, пока это возможно:
- случайно выберите из банки два зерна и
- если они одного цвета, отбросьте их, но положите в банку другое черное зерно (имеется достаточный запас черных зерен, чтобы делать это);
- если они разного цвета, поместите белое зерно обратно в банку и отбросьте черное зерно.
Выполнение этого процесса уменьшает количество зерен в банке на единицу. Повторение процесса должно прекратиться, когда в банке останется всего одно зерно, так как тогда нельзя уже выбрать два зерна. Можно ли что-то сказать о цвете оставшегося зерна, если известно, сколько вначале в банке было черных и белых зерен?
Задача 7.77. Замыкание кривой. Двое играют на листе клетчатой бумаги произвольной
формы и размера в следующую игру. Игроки делают ходы поочередно и начинает
игрок  . Ход игрока
. Ход игрока  состоит в том, что он соединяет горизонтальным или
вертикальным отрезком два соседних узла решетки, проводя непрерывную линию
по границе одного из квадратиков (клеточек) бумаги. Ход игрока
состоит в том, что он соединяет горизонтальным или
вертикальным отрезком два соседних узла решетки, проводя непрерывную линию
по границе одного из квадратиков (клеточек) бумаги. Ход игрока  сводится
к проведению пунктирной линии, обладающей теми же свойствами. Проводить линию
по уже нарисованной противником нельзя.
сводится
к проведению пунктирной линии, обладающей теми же свойствами. Проводить линию
по уже нарисованной противником нельзя.
Игрок  выигрывает, если ему удается получить полностью замкнутую кривую,
состоящую из непрерывных линий. Если игрок
выигрывает, если ему удается получить полностью замкнутую кривую,
состоящую из непрерывных линий. Если игрок  не сумеет получить замкнутую
кривую, то считается, что победил игрок
не сумеет получить замкнутую
кривую, то считается, что победил игрок  . Существует ли стратегия,
гарантирующая выигрыш на произвольной доске для одного из игроков?
. Существует ли стратегия,
гарантирующая выигрыш на произвольной доске для одного из игроков?

