НОУ ИНТУИТ | Основы дискретной математики. Лекция 7: Язык логики предикатов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 21.08.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Тверской государственный университет

|

Вам нравится? Нравится 37 студентам

| Поделиться |

Поддержать программу

Язык логики предикатов

В определениях формальных языков, таких, как логические языки или языки программирования, выделяют два основных аспекта: синтаксис и семантику. Синтаксис \index{Синтаксис} определяет алфавит, из символов которого строятся выражения языка, и правила, выделяющие из множества всех слов в данном алфавите правильно построенные выражения. Для логических языков такие выражения обычно называются формулами, а для языков программирования - программами. Семантика \index{Семантика} занимается определением смысла, значения этих выражений. Для формул большинства логических языков значением является одно из истиностных значений: 1 (истина) или 0 (ложь), которое приписывается формуле в зависимости от интерпретации входящих в нее символов языка. Например, значения формул логики высказываний зависят от значений входящих в них булевых переменных. Значения формул определяемой в этом параграфе логики предикатов будут зависеть от интерпретации предикатов и функций языка, а также от значений входящих в эти формулы переменных.

Синтаксис: формулы логики предикатов

Формулы языка логики предикатов включают в себя символы (имена) предикатов из некоторого Множества ${\bf P}= \{ P_1^{(n_1)}, P_2^{(n_2)},\ldots , P_k^{(n_k)}, \ldots \}$ , символы (имена) функций из некоторого множества ${\bf F}= \{ f_1^{(m_1)}, f_2^{(m_2)}, \ldots , f_j^{(m_j)},\ldots \}$ , символы (имена) констант из некоторого множества C={ c₁, c₂, ... 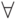}, логические связки $\{ \neg , \wedge , \vee , \to \}$ , кванторы всеобщности $\forall$ и существования $\exists$ и вспомогательные символы (скобки, запятые). Первые три множества образуют сигнатуру языка: $\Sigma = < P, F, C>$ . \index{Сигнатура} Зафиксируем некоторое счетное множество объектных переменных Var (такие переменные также называют предметными или индивидными ). Они предназначены для обозначения элементов множества (объектов), на котором определены функции и предикаты ; обычно в таком качестве используют латинские буквы x, y,z,u,v,w, x_i, y_j, z_k и т.п. В каждой формуле будет использоваться конечное число переменных, так что счётного набора переменных нам хватит. Чтобы не возникла путаница, будем считать, что переменные отличны от всех имен констант, функций и предикатов.

Определим понятие терма данной сигнатуры 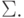$\Sigma.$

Определение 7.1. Терм. Термом называется выражение, состоящее из переменных, запятых, скобок и символов сигнатуры, которое можно построить по следующим правилам.

Объектная переменная из Var есть терм.
Символ константы из C есть терм.
Если t₁,...,t_k - термы, а f^(k) - символ функции из F, то f(t₁,...,t_k) есть терм.

Термы, не содержащие переменных, назовем замкнутыми.

Термы служат для задания объектов. Замкнутые термы задают объекты непосредственно.

Пример 7.1. Пусть F={отец⁽¹⁾, лучший_друг⁽¹⁾, зарплата⁽¹⁾, + ⁽²⁾}, а C= {"Петр", "Джон", "Ольга", 0, 1, 2, ... }.

Тогда самый простой способ задать объект - это указать соответствующую константу, например, "Петр", "Джон", 0, 1, 47, .... Терм +(17, 25) задает объект 42, терм лучший_ друг(отец("Петр" ) ) задает объект - лицо, являющееся лучшим другом отца объекта "Петр", а терм зарплата(лучший_ друг(отец("Петр") ) ) задает объект-число, представляющее зарплату этого лица. Значениями переменных также являются объекты. Поэтому термы с переменными задают конкретные объекты при подстановке значений вместо переменых. Приведем еще несколько примеров термов данной сигнатуры: x, отец (x), зарплата(лучший_ друг(отец(отец(z)))), +(зарплата(лучший_ друг(отец(z)) ), +(зарплата ("Ольга" ), 1000)), отец(5), +(отец("Ольга" ), 1000)) . Отметим, что последние два терма построены в соответствии с нашими правилами, но неясно, какие объекты они могут задавать. Это зависит от определения функции отец на числах и функции + на парах аргументов вида (Лицо, Число). Часто во множество объектов включают специальный объект "ОШИБКА", который является значением функций на некорректных аргументах.

Выражения x +10, отец ("Джон", "Петр"), +(100)}, лучший_друг("Мария") термами данной сигнатуры не являются. (Определите почему.)

Определение 7.2. Атомная формула.

Если t₁ и t₂ - термы, то выражение (t₁ = t₂) является атомной формулой.
Любой предикатный 0 -местный символ из P является атомной формулой.
Если P^(k) (k >= 1) - предикатный k -местный символ из P, а t₁,...,t_k - термы, то выражение P(t₁,...,t_k) является атомной формулой.

Пример 7.2. Рассмотрим сигнатуру 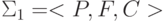$\Sigma _{1} = < P, F, C>$ , в которой P= { живут_рядом⁽²⁾, сын⁽²⁾, дочь⁽²⁾, родственники⁽²⁾, человек⁽¹⁾, число⁽¹⁾, <= ⁽²⁾}, а функции F и константы C определены в примере выше.

Тогда следующие выражения являются атомными формулами: "Джон" = "Петр", "Петр" = 6, отец("Ольга") = "Петр", +(3,5) = +(1, +(6,1)), зарплата(лучший_ друг(отец(z)) = 5000}, живут_рядом("Джон","Ольга"), сын( "Джон","Ольга"), дочь("Ольга", x), родственники(лучший_ друг("Джон"), отец( x)) и т.п.

Формулы логики предикатов строятся по таким правилам:

Определение 7.3. Формула.

Всякая атомная формула есть формула.
Если $\phi$ - формула, то $\neg \varphi$ - формула.
Если $\phi$ и $\psi$ - формулы, то выражения $(\varphi \wedge \psi )$ , $(\varphi \vee \psi )$ , $(\varphi \to \psi )$ также являются формулами.
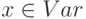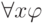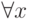Если $\phi$ - формула, а $x \in Var$ - объектная переменная, то выражения $\forall x \varphi$ и $\exists x \varphi$ являются формулами (в этом случае $\forall x\varphi$ и $\exists x\varphi$ называются областью действия квантора $\forall x$ или $\exists x$ соответственно).

Понятие подформулы для формул логики предикатов определяется естественным образом. Во-первых, сама формула является своей подформулой. Во-вторых, если формула имеет вид 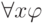$\neg \varphi$ , $\forall x \varphi$ или $\exists x \varphi$ , то ее подформулами также являются все подформулы формулы $\phi,$ а если она имеет вид $(\varphi \wedge \psi )$ , $(\varphi \vee \psi )$ или $(\varphi \to \psi )$ , то ее подформулами также являются все подформулы формул $\phi$ и $\psi.$

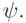
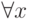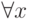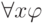Определим также понятия связанных и свободных переменных формулы. Вхождение переменной x в формулу $\phi$ называется связанным, если оно входит в область действия некоторого квантора $\forall x$ или $\exists x$ . В противном случае, оно называется свободным. Квантор $\forall x$ ( $\exists x$ ) связывает в формуле $\forall x \varphi$ ( $\exists x \varphi$ ) все свободные вхождения переменной x в подформулу $\phi.$

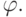
Пусть в некоторой сигнатуре имеются два двуместных предиката P⁽²⁾, Q⁽²⁾. Тогда в формуле

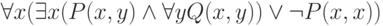
$\forall x (\exists x(P(x,y) \wedge \forall y Q( x, y )) \vee \neg P(x,x))$

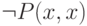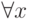оба вхождения x в подформулу $(P(x,y) \wedge \forall y Q( x, y ))$ связаны квантором $\exists x$ , первое вхождение y является свободным, а второе - связано квантором $\forall y$ . Оба вхождения x в подформулу $\neg P(x,x)$ связаны квантором $\forall x$ .

Переменная называется свободной (связанной) в формуле, если у нее есть хоть одно свободное (связанное) вхождение в эту формулу. Формула, у которой нет свободных переменных, называется замкнутой. Отметим, что переменная может быть одновременно связанной и свободной в данной формуле.

Пример 7.3. Рассмотрим примеры формул в сигнатуре $\Sigma _{1}$ из примера 7.2:

$\varphi_1= \varphi_1= \forall x( \textit{человек(x)} \rightarrow \exists y (\textit{человек(y)} \wedge \textit{живут\_рядом( x,y ) ) }$

В этой формуле все вхождения переменных x и y являются связанными и, следовательно, 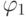$\varphi _{1}$ - замкнутая формула. Содержательно, она утверждает, что у всякого человека имется человек-сосед. Понятно, что истинность этого утверждения не зависит от имен переменных, использованных в формуле.
$\varphi_2= \exists y[\textit{человек(y)} \wedge( \forall x \ \textit{родственники( x, y )}\vee \\ \vee \neg \textit{живут\_рядом}( x,y ) \wedge (\textit{зарплата(y)} \geq 35) )]$

В формуле 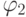$\varphi _{2}$ все вхождения переменной y являются связанными, первое вхождение x также связано, а второе вхождение x свободно, так как не входит в область действия квантора 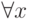$\forall x$ . Таким образом x в 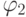$\varphi _{2}$ является связанной и свободной. Эта формула утверждает что имеется такой человек, который состоит в родственных отношениях со всеми или не живет рядом с x и имеет зарплату >= 35. Ясно, что истинность этой формулы зависит от значения свободной переменной x.