|
Это в лекции 3. |
Полные системы функций и теорема Поста
Критерий полноты (теорема Поста)
Оказывается, что всякая система, не содержащаяся внутри одного из указанных пяти классов полна.
Теорема 5.2. (Теорема Поста о полноте)
Система булевых функций F является полной тогда и только тогда, когда она не содержится ни в одном из
классов 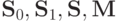 и
и 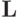 ,
т.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная
функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.
,
т.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная
функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.
Доказательство. Необходимость условия теоремы непосредственно следует из установленного выше следствия 5.1.1.
Для доказательства достаточности предположим, что F
Содержит не сохраняющую 0 функцию 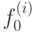 , не сохраняющую 1 функцию
, не сохраняющую 1 функцию 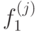 , несамодвойственную функцию
, несамодвойственную функцию 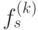 , немонотонную функцию
, немонотонную функцию 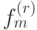 и нелинейную функцию
и нелинейную функцию  . Покажем,
что с помощью этих функций всегда можно выразить функции одной из двух уже известных нам полных систем:
. Покажем,
что с помощью этих функций всегда можно выразить функции одной из двух уже известных нам полных систем: 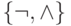 или
или 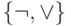 . Для этого установим, что:
. Для этого установим, что:
- используя f0, f1 и fs, можно выразить константы 0 и 1;
- с помощью констант из fm можно получить отрицание
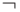 ;
; - с помощью констант и отрицания из fl можно получить конъюнкцию
 или дизъюнкцию
или дизъюнкцию 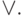
Лемма 5.1. Формулами, построенными из функций f0, f1 и fs,можно задать константы 0 и 1.
Доказательство.. Рассмотрим два возможных значения  на наборе аргументов,
состоящем из одних единиц.
на наборе аргументов,
состоящем из одних единиц.
Случай 1. f0(1, ... , 1)= 0. Рассмотрим функцию g(X),
заданную формулой f0(X,... , X). Тогда, очевидно, g(0) =f0(0,
... , 0) =1, а g(1) = f0(1, ... , 1)= 0. Таким образом, получили отрицание: 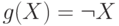 .
Так как
.
Так как 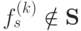 , то для некоторого набора значений аргументов
, то для некоторого набора значений аргументов 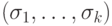 имеет место равенство
имеет место равенство 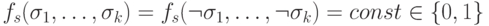 .
Положим тогда
.
Положим тогда 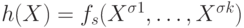 (такая подстановка переменной X1 и ее отрицания X0 возможна,
так как мы уже получили отрицание).
Тогда h - это константа const. Действительно,
(такая подстановка переменной X1 и ее отрицания X0 возможна,
так как мы уже получили отрицание).
Тогда h - это константа const. Действительно, 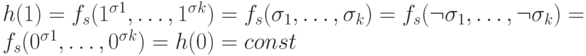 .
Другая константа тогда задается формулой
.
Другая константа тогда задается формулой 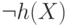 .
.
Случай 2. f0(1, ... , 1)= 1. В этом случае формула f0(X,...
, X) задает функцию g(X), тождественно равную 1, а формула f1(g(X), ... , g(X))
задает функцию h(X), тождественно равную 0.
Действительно,  для любого
для любого 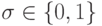 .
.
Лемма 5.2. Формулами, построенными из констант 0 и 1 и немонотонной функции 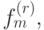 можно задать отрицание
можно задать отрицание 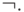
Доказательство. Так как 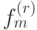 немонотонна, то имеются два
разных набора аргументов
немонотонна, то имеются два
разных набора аргументов 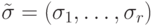 и
и 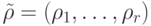 таких, что
для всех
таких, что
для всех ![j \in [1,r] \sigma _{j} \ge \rho _{j}](/sites/default/files/tex_cache/feced7dcd229ec9460b7aa7efb79799c.png) и при
этом
и при
этом 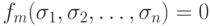 ,
а
,
а 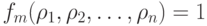 .
Пусть i1, ... , il - это все индексы, для которых
.
Пусть i1, ... , il - это все индексы, для которых 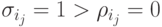 . Так как
. Так как  , то l >= 1. Определим последовательность из (l+1) -го
набора аргументов
, то l >= 1. Определим последовательность из (l+1) -го
набора аргументов 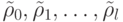 следующим образом:
следующим образом: 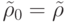 , а
далее каждый набор
, а
далее каждый набор 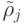 получется из
предыдущего
получется из
предыдущего 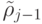 заменой ij -ой координаты с 0 на 1. Таким образом, последний из этих наборов
заменой ij -ой координаты с 0 на 1. Таким образом, последний из этих наборов  совпадает с
совпадает с 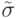 .
Рассмотрим значения функции fm на
этих наборах:
.
Рассмотрим значения функции fm на
этих наборах: 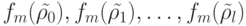 .
Так как первое из них
.
Так как первое из них 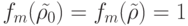 ,
а последнее
,
а последнее 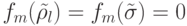 , то
найдутся два соседних
набора
, то
найдутся два соседних
набора 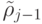 и
и 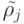 таких,
что
таких,
что 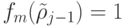 , а
, а 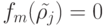 .
Они отличаются только ij -ой координатой.
Пусть
.
Они отличаются только ij -ой координатой.
Пусть  ,
a
,
a  . Положим тогда
. Положим тогда 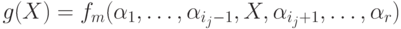 . Тогда
. Тогда 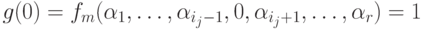 , a
, a 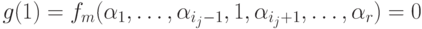 . Следовательно,
. Следовательно, 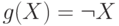 .
.
Лемма 5.3. Формулами, построенными из констант 0 и 1, отрицания 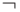 и нелинейной
функции
и нелинейной
функции 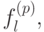 можно задать дизъюнкцию
можно задать дизъюнкцию  или конъюнкцию
или конъюнкцию 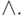
Доказательство. Так как 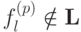 , то в представляющий ее
многочлен Жегалкина обязательно входит слагаемое вида
, то в представляющий ее
многочлен Жегалкина обязательно входит слагаемое вида  .
Выберем самое короткое из таких слагаемых и рассмотрим функцию
.
Выберем самое короткое из таких слагаемых и рассмотрим функцию 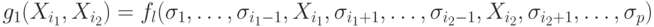 , где
, где 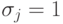 при
при 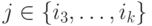 и
и  в остальных случаях.
При такой подстановке констант многочлен Жегалкина для g(X1,X2) = g1(X1,X2)
имеет вид:
в остальных случаях.
При такой подстановке констант многочлен Жегалкина для g(X1,X2) = g1(X1,X2)
имеет вид: 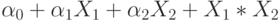 ,
где
,
где 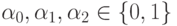 .
Таким образом, всего возможно 8 вариантов. Рассмотрим 4 из них в случае, когда
.
Таким образом, всего возможно 8 вариантов. Рассмотрим 4 из них в случае, когда 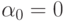 . Тогда
. Тогда
- при
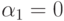 и
и 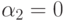 получаем, что
получаем, что 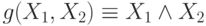 ;
; - при
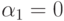 и
и 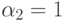 получаем, что
получаем, что 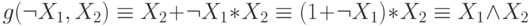 ;
; - при
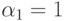 и
и 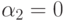 получаем, что
получаем, что 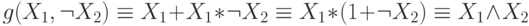 ;
; - при
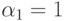 и
и 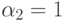 имеем
имеем 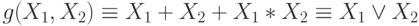 .
.
Остальные 4 варианта в случае, когда 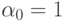 , получаются как отрицания
соответствующих вариантов для
, получаются как отрицания
соответствующих вариантов для 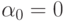 .
.
Из приведенных трех лемм, очевидно, следует достаточность условия теоремы Поста.
Пример 5.2. Рассмотрим набор функций f, g и h, представленный в следующей таблице:
| X1 | X2 | X3 | f | g | h |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
Функция f, очевидно, не сохраняет 0 и 1, но является самодвойственной.
Функция g(X1,X2,X3)= 1+X1+X2 + X1
* X3 + X1 * X2 * X3
является несамодвойственной, немонотонной и нелинейной.
По лемме 5.1 получаем, что 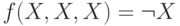 ,
функция
,
функция 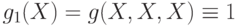 , а функция
, а функция 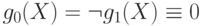 .
Подставив X2=0 в g получим g3(X1,X3)=
g(X1,0,X3)= 1 + X1 + X1 * X3.
Тогда
.
Подставив X2=0 в g получим g3(X1,X3)=
g(X1,0,X3)= 1 + X1 + X1 * X3.
Тогда  .
Таким образом, мы с помощью f и g сумели выразить
обе функции полной системы
.
Таким образом, мы с помощью f и g сумели выразить
обе функции полной системы 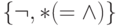 и, следовательно, система функций {f,
g } полная.
и, следовательно, система функций {f,
g } полная.
Определение 5.5. Полная система функций называется минимальной полной системой или базисом, если после удаления из нее любой функции она перестает быть полной .
Например, система 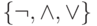 не является базисом,
а каждая из систем
не является базисом,
а каждая из систем 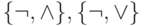 является. Мы
уже знаем, что имеются полные системы,
состоящие из одной функции (например, система { | } ). Они,
конечно, являются базисами.
Имеются и полные системы, включающие 3 функции, например, система { 1,
*, +}, на которой основаны многочлены Жегалкина (отметим, что константу 0 можно выразить как
1+1). Из теоремы Поста следует, что никакая минимальная система не содержит более 5 функций. Оказывается,
что для полноты всегда достаточно четырех функций.
является. Мы
уже знаем, что имеются полные системы,
состоящие из одной функции (например, система { | } ). Они,
конечно, являются базисами.
Имеются и полные системы, включающие 3 функции, например, система { 1,
*, +}, на которой основаны многочлены Жегалкина (отметим, что константу 0 можно выразить как
1+1). Из теоремы Поста следует, что никакая минимальная система не содержит более 5 функций. Оказывается,
что для полноты всегда достаточно четырех функций.
Теорема 5.3. Во всяком базисе F содержится не более 4-х функций.
Доказательство. Действительно, по теореме Поста в базисе  имеется функция
имеется функция 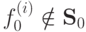 . Поэтому f0(0,0, ...,
0)
=1. Если она хотя бы на одном наборе значений аргументов принимает значение 0, то она немонотонна,
т.е.
. Поэтому f0(0,0, ...,
0)
=1. Если она хотя бы на одном наборе значений аргументов принимает значение 0, то она немонотонна,
т.е. 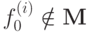 . В противном случае, f0
на всех наборах значений аргументов равна 1. Но тогда она несамодвойственна , так как f0(0,
0, ..., 0)=1 = f0(1,1,..., 1). Во всех случаях
. В противном случае, f0
на всех наборах значений аргументов равна 1. Но тогда она несамодвойственна , так как f0(0,
0, ..., 0)=1 = f0(1,1,..., 1). Во всех случаях 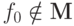 или
или 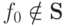 и, следовательно, в системе F
содержится не более 4-х функций.
и, следовательно, в системе F
содержится не более 4-х функций.
Может быть, в минимальной системе можно обойтись тремя функциями? Это не
так. Рассмотрим, например, систему 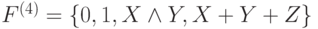 . В этой системе,
. В этой системе, 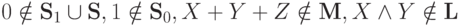 . Легко проверить, что при удалении любой из функций система F(4)
перестает быть полной. Таким образом, теорема 5.3 дает наилучшую верхнюю оценку числа функций
в базисе.
. Легко проверить, что при удалении любой из функций система F(4)
перестает быть полной. Таким образом, теорема 5.3 дает наилучшую верхнюю оценку числа функций
в базисе.
Замечание. Е. Пост в работах, опубликованных в 1921 и 1941 гг.
не только установил критерий полноты, но и описал структуру всех
замкнутых классов функций в  . Он показал, что число таких классов
счетно и что в каждом из них имеется собственный конечный базис.
. Он показал, что число таких классов
счетно и что в каждом из них имеется собственный конечный базис.
Задачи
Задача 5.1. Докажите полноту системы 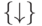 , включающей только стрелку Пирса,
непосредственно выразив через нее отрицание, дизъюнкцию и конъюнкцию.
, включающей только стрелку Пирса,
непосредственно выразив через нее отрицание, дизъюнкцию и конъюнкцию.
Задача 5.2. Определите принадлежность каждой из функций f1, f2,
f3, f4 и f5, представленных в таблице 5.1,
каждому из классов 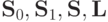 и
и  .
.
Задача 5.3. Используя результаты задачи 5.2, определите, какие из троек функций, представленных в таблице 5.1, являются полными системами. Имеются ли среди них полные системы из двух функций? Из одной функции?
Задача 5.4. Проверьте полноту системы функций {g, h},
представленных в таблице 5.2. Если она полна, выразите с помощью этих функций обе константы, отрицание 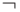 и импликацию
и импликацию 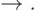
Задача 5.5. Докажите, что система 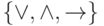 не является полной. Можно
ли ее сделать полной, добавив некоторую константу?
не является полной. Можно
ли ее сделать полной, добавив некоторую константу?
Задача 5.6. Выразите функции 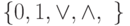 с помощью формул, построенных из функций полной системы
с помощью формул, построенных из функций полной системы 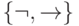 .
.
Задача 5.7. Определите количество функций из 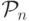 , принадлежащих
каждому из классов
, принадлежащих
каждому из классов  и
и 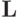 .
.
Задача 5.8. Доказать, что для монотонных функций 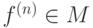 справедливо
представление
справедливо
представление 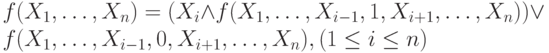 .
Вывести отсюда (индукцией по n ), что для всякой монотонной функции, отличной от константы,
существует задающая ее ДНФ, не содержащая отрицаний переменных.
.
Вывести отсюда (индукцией по n ), что для всякой монотонной функции, отличной от константы,
существует задающая ее ДНФ, не содержащая отрицаний переменных.
Задача 5.9. Докажите, что число монотонных функций в 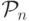 не меньше
не меньше ![2^{C_n^{[n/2]}}](/sites/default/files/tex_cache/1147a3fb84a8fb500361d29e84ef09cb.png) .
.
Задача 5.10. Найдите все базисы, которые можно получить,
удаляя функции из системы 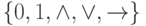 .
.
Задача 5.11. Найти число булевых функций от n переменных, являющихся одновременно самодвойственными и линейными.
Задача 5.12. Найти число булевых функций от n переменных, являющихся одновременно монотонными и линейными.
Задача 5.13. Доказать, что если f(X1, ..., Xn) - линейная
функция, отличная от константы, то  . Верно ли обратное?
. Верно ли обратное?
