|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Принятие решений на основе моделей обеспечения качества
Риск поставщика и риск потребителя, приемочный и браковочный уровни дефектности. С оперативной характеристикой связаны важные понятия приемочного и браковочного уровней дефектности, а также понятия "риск поставщика" и "риск потребителя". Чтобы ввести эти понятия, на оперативной характеристике выделяют две характерные точки, делящие входные уровни дефектности на три зоны (области) - 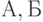 и
и  . В зоне
. В зоне  почти всегда все хорошо, а именно - почти всегда экологическая обстановка признается благополучной, почти все партии принимаются. В зоне
почти всегда все хорошо, а именно - почти всегда экологическая обстановка признается благополучной, почти все партии принимаются. В зоне  , наоборот, почти всегда все плохо, а именно - почти всегда экологический контроль констатирует экологические нарушения, почти все партии бракуются. Зона
, наоборот, почти всегда все плохо, а именно - почти всегда экологический контроль констатирует экологические нарушения, почти все партии бракуются. Зона  - буферная, переходная, промежуточная, в ней как вероятность приемки, так и вероятность браковки заметно отличаются от 0 и 1. Для задания границ между зонами выбирают два малых числа-риск поставщика (производителя, предприятия)
- буферная, переходная, промежуточная, в ней как вероятность приемки, так и вероятность браковки заметно отличаются от 0 и 1. Для задания границ между зонами выбирают два малых числа-риск поставщика (производителя, предприятия)  и риск потребителя (заказчика, системы экологического контроля)
и риск потребителя (заказчика, системы экологического контроля)  , при этом границы между зонами задают два уровня дефектности - приемочный
, при этом границы между зонами задают два уровня дефектности - приемочный  и браковочный
и браковочный  , определяемые из уравнений
, определяемые из уравнений
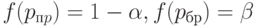 |
( 6) |
Таким образом, если входной уровень дефектности не превосходит  , то вероятность забракования партии мала, т.е. не превосходит
, то вероятность забракования партии мала, т.е. не превосходит  . Приемочный уровень дефектности выделяет зону
. Приемочный уровень дефектности выделяет зону  значений входного уровня дефектности, в которой нарушения экологической безопасности почти всегда не отмечаются, партии почти всегда принимаются, т.е. соблюдаются интересы проверяемого предприятия (в экологии), поставщика (при контроле качества). Это - зона комфортности для поставщика. Если он обеспечивает работу (входной уровень дефектности) в этой зоне, то его практически никогда никто не потревожит.
значений входного уровня дефектности, в которой нарушения экологической безопасности почти всегда не отмечаются, партии почти всегда принимаются, т.е. соблюдаются интересы проверяемого предприятия (в экологии), поставщика (при контроле качества). Это - зона комфортности для поставщика. Если он обеспечивает работу (входной уровень дефектности) в этой зоне, то его практически никогда никто не потревожит.
Если же входной уровень дефектности больше браковочного уровня дефектности  , то нарушения почти наверняка фиксируются, партия почти всегда бракуется, т.е. экологи узнают о нарушениях, потребитель оказывается защищен от попадания к нему партий со столь высоким уровнем брака. Поэтому можно сказать, что в зоне
, то нарушения почти наверняка фиксируются, партия почти всегда бракуется, т.е. экологи узнают о нарушениях, потребитель оказывается защищен от попадания к нему партий со столь высоким уровнем брака. Поэтому можно сказать, что в зоне  соблюдаются интересы потребителей - брак к ним не попадает.
соблюдаются интересы потребителей - брак к ним не попадает.
При выборе плана контроля часто начинают с выбора приемочного и браковочного уровней дефектности. При этом выбор конкретного значения приемочного уровня дефектности отражает интересы поставщика, а выбор конкретного значения браковочного уровня дефектности - интересы потребителя. Можно доказать (см. ниже), что для любых положительных чисел  и
и  и любых входных уровней дефектности
и любых входных уровней дефектности  и
и  , причем
, причем  меньше
меньше  , найдется план контроля
, найдется план контроля 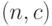 такой, что его оперативная характеристика
такой, что его оперативная характеристика 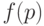 удовлетворяет неравенствам
удовлетворяет неравенствам
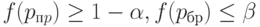
При практических расчетах обычно принимают 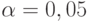 (т.е. 5%) и
(т.е. 5%) и 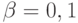 (т.е. 10%).
(т.е. 10%).
В качестве примера вычислим приемочный и браковочный уровни дефектности для плана  . Из формул (4) и (6) вытекает, что
. Из формул (4) и (6) вытекает, что
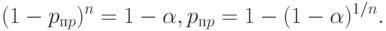
Поскольку риск поставщика  мал, то из известного соотношения математического анализа
мал, то из известного соотношения математического анализа
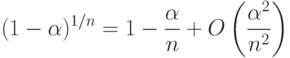
вытекает приближенная формула
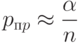
Для браковочного уровня дефектности имеем
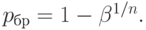
При практическом применении методов статистического приемочного контроля аналитическими формулами, имеющими обозримый вид лишь для отдельных видов планов, не пользуются. Для нахождения приемочных и браковочных уровней дефектности планов контроля вместо них применяют численные компьютерные алгоритмы или заранее составленные таблицы. Такие таблицы имеются в нормативно-технической документации или научно-технических публикациях.
Предел среднего выходного уровня дефектности.Обсудим судьбу забракованной партии продукции. В зависимости от ситуации эта судьба может быть разной. Партия может быть утилизирована. Например, забракованная партия гвоздей может быть направлена на переплавку. У партии может быть понижена сортность, и она может быть продана по более низкой цене (при этом результаты выборочного контроля будут использованы не только для констатации того, что не выдержан заданный уровень качества, но и для оценки реального уровня качества). Наконец, партия продукции может быть подвергнута сплошному контролю (для этого обычно привлекают инженеров из всех заводских служб). При сплошном контроле все дефектные изделия обнаруживаются и либо исправляются на месте, либо извлекаются из партии. В результате в партии остаются только годные изделия. Такая процедура называется "контроль с разбраковкой".
При среднем входном уровне дефектности  и применении контроля с разбраковкой с вероятностью
и применении контроля с разбраковкой с вероятностью 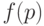 партия принимается (и уровень дефектности в ней по-прежнему равен
партия принимается (и уровень дефектности в ней по-прежнему равен  ) и с вероятностью
) и с вероятностью 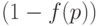 бракуется и подвергается сплошному контролю, в результате чего к потребителю поступают только годные изделия. Следовательно, по формуле полной вероятности средний выходной уровень дефектности равен
бракуется и подвергается сплошному контролю, в результате чего к потребителю поступают только годные изделия. Следовательно, по формуле полной вероятности средний выходной уровень дефектности равен

Средний выходной уровень дефектности 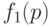 равен 0 при
равен 0 при  и
и  , положителен на интервале (0;1), а потому достигает на нем максимума, который в теории статистического контроля называется пределом среднего выходного уровня дефектности (сокращенно ПСВУД):
, положителен на интервале (0;1), а потому достигает на нем максимума, который в теории статистического контроля называется пределом среднего выходного уровня дефектности (сокращенно ПСВУД):

Пример. Рассмотрим план  . Для него
. Для него 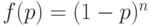 и
и 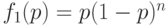 . Чтобы найти ПСВУД, надо приравнять 0 производную среднего выходного уровня дефектности по среднему входному уровню дефектности:
. Чтобы найти ПСВУД, надо приравнять 0 производную среднего выходного уровня дефектности по среднему входному уровню дефектности:
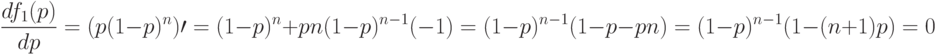
В полученном уравнении корень  соответствует минимуму, а не максимуму. Поскольку непрерывная функция на замкнутом отрезке достигает максимума, то максимум достигается при
соответствует минимуму, а не максимуму. Поскольку непрерывная функция на замкнутом отрезке достигает максимума, то максимум достигается при
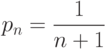
Следовательно,
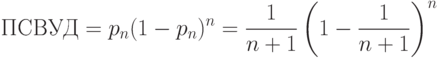 |
( 7) |
По выражению (7) могут быть проведены конкретные расчеты. Однако оно довольно громоздко. Его можно упростить, используя один замечательный предел из курса математического анализа, а именно:
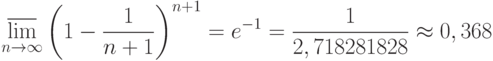 |
( 8) |
Сравнивая соотношения (7) и (8), видим, что

Первая скобка равна 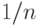 , а вторая согласно соотношению (8) приближается к 0,368 при росте объема выборки. Поэтому получаем простую асимптотическую формулу
, а вторая согласно соотношению (8) приближается к 0,368 при росте объема выборки. Поэтому получаем простую асимптотическую формулу
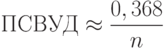
Для более сложных планов ПСВУД рассчитывают с помощью более или менее сложных компьютерных программ.
При проведенном выше рассмотрении основ статистического контроля расчетные формулы удалось получить лишь для простейших планов, в основном для планов вида  . Если ослабить требования и рассчитывать не на точные формулы, а на асимптотические, при
. Если ослабить требования и рассчитывать не на точные формулы, а на асимптотические, при 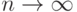 , то можно справиться и с одноступенчатыми планами вида
, то можно справиться и с одноступенчатыми планами вида 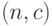 .
.
Асимптотическая теория одноступенчатых планов. Пусть  - число дефектных единиц продукции в выборке объема
- число дефектных единиц продукции в выборке объема  . Как уже отмечалось, распределение
. Как уже отмечалось, распределение  является биномиальным и имеет вид
является биномиальным и имеет вид
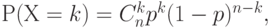
где 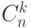 - число сочетаний из
- число сочетаний из  элементов по
элементов по  , а
, а  - входной уровень дефектности.
- входной уровень дефектности.
Пусть используется одноступенчатый план контроля 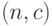 . Тогда оперативная характеристика этого плана имеет вид
. Тогда оперативная характеристика этого плана имеет вид
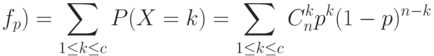
Пусть 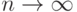 Тогда по Закону Больших Чисел теории вероятностей (по теореме Бернулли)
Тогда по Закону Больших Чисел теории вероятностей (по теореме Бернулли)

(сходимость по вероятности). Значит, если  окажется заметно больше входного уровня дефектности
окажется заметно больше входного уровня дефектности  , то партии будут почти всегда приниматься, а если
, то партии будут почти всегда приниматься, а если  окажется заметно меньше входного уровня дефектности
окажется заметно меньше входного уровня дефектности  , то партии будут почти всегда отклоняться. Ситуация будет нетривиальной только там, где величины
, то партии будут почти всегда отклоняться. Ситуация будет нетривиальной только там, где величины  и
и  близки друг к другу.
близки друг к другу.
Хотя оперативная характеристика рассчитывается с помощью сумм биномиальных вероятностей, анализировать эти суммы затруднительно. Поэтому целесообразно найти для нее приближение с помощью теоремы Муавра-Лапласа. Имеем цепочку тождественных преобразований:
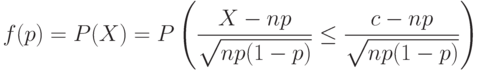
Справа стоит именно то выражение, которое участвует в теореме Муавра-Лапласа. Воспользовавшись равномерной сходимостью в этой теореме, можно записать, что
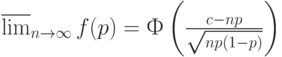
где 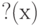 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
Последняя формула позволяет указать асимптотические выражения для приемочного и браковочного уровней дефектности. Действительно, согласно определениям этих понятий
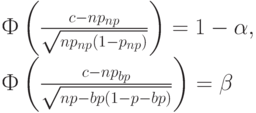 |
( 9) |
откуда с помощью элементарных преобразований получаем, что
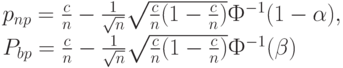 |
( 10) |
Так как величины  и
и  близки друг к другу, то при переходе от формулы (9) к формуле (10) в подкоренных выражениях приемочный и браковочный уровни дефектности заменены на
близки друг к другу, то при переходе от формулы (9) к формуле (10) в подкоренных выражениях приемочный и браковочный уровни дефектности заменены на  (с точностью до бесконечно малых более высокого порядка).
(с точностью до бесконечно малых более высокого порядка).
Поскольку при практическом применении статистического приемочного контроля, как уже отмечалось, принимают 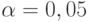 ,
, 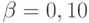 , то в предыдущие формулы следует подставить
, то в предыдущие формулы следует подставить 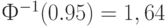 и
и 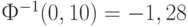 Итак, итоговые формулы для приемочного и браковочного уровней дефектности имеют вид
Итак, итоговые формулы для приемочного и браковочного уровней дефектности имеют вид
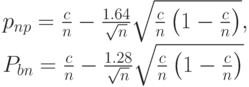
Перейдем к задаче синтеза. Пусть заданы приемочный и браковочный уровни дефектности. Требуется построить одноступенчатый план, имеющий эти характеристики. Из формул (9) следует, в частности, что
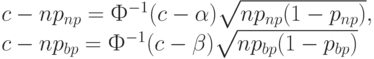 |
( 11) |
Вычитая из первого уравнения второе, получаем, что
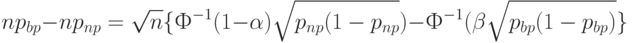
Следовательно, оценка  необходимого объема выборки имеет вид
необходимого объема выборки имеет вид
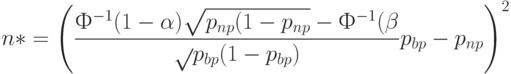
Для стандартных значений рисков 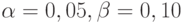 имеем:
имеем:
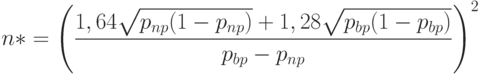 |
( 12) |
С помощью уравнений (11) нетрудно найти оценку  приемочного числа, заменив неизвестный объем выборки на его оценку
приемочного числа, заменив неизвестный объем выборки на его оценку  . Будем использовать оценку
. Будем использовать оценку
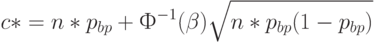
Для стандартного значения 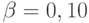 имеем
имеем
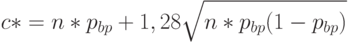 |
( 13) |
Итак, по формуле (12) можно рассчитать оценку объема выборки, затем по формуле (13) найти оценку приемочного числа. Необходимо отметить, что результаты расчетов по рассматриваемым асимптотическим формулам отнюдь не всегда дают целые числа, поэтому необходима корректировка полученных результатов.
Полученные формулы позволяют решить сформулированную выше задачу - по заданным приемочному и браковочному уровням дефектности подобрать такой одноступенчатый план контроля, что его оперативная характеристика 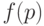 удовлетворяет неравенствам
удовлетворяет неравенствам
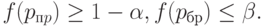
Поэтому при практической работе корректировка асимптотических результатов должна быть направлена на выполнение указанных неравенств.
Пример. Пусть  . Тогда по формуле (12) оценка объема выборки равна
. Тогда по формуле (12) оценка объема выборки равна
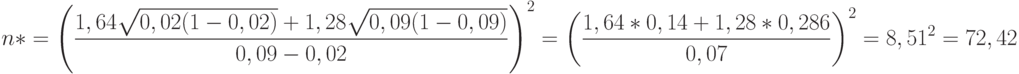
Полученное число не является натуральным, поэтому вполне естественно откорректировать объем выборки до ближайшего целого, т.е. до 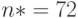 .
.
Оценку приемочного числа находим по формуле (13):
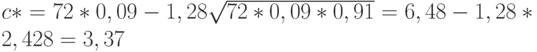
Полученное число не является целым, поэтому в качестве приемочного числа надо взять ближайшее целое, т.е. до 3.
Если объем выборки округлить до 73, то аналогично получим
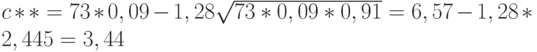
При округлении снова получаем 3.
С помощью первого из уравнений (11) можно построить оценку с* на основе приемочного уровня дефектности:

Подставив конкретные значения, получим практически ту же оценку, что и раньше:
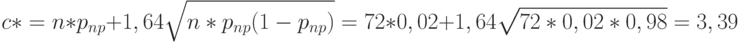
Итак, в результате асимптотических расчетов найден одноступенчатый план (72, 3).

