Алгоритмы: частично рекурсивные функции

Леммы о рекурсивных функциях

В этом параграфе мы установим примитивную (частичную) рекурсивность некоторых важных классов функций - таблиц и нумераций, и расширим возможности определения функций с помощью суммирования, произведения, разбора случаев и взаимной рекурсии.

Лемма 8.1. Рекурсивность табличных функций. Пусть всюду определенная функция f(x) на всех аргументах, кроме конечного числа, равна некоторой константе c (такую функцию назовем табличной). Тогда она является примитивно рекурсивной.

Доказательство Пусть для функции f из условия леммы . Доказательство проведем индукцией по n_f.

При n_f=0 функция f является постоянной и поэтому примитивно рекурсивной (пример 8.1).

Предположим что все табличные функции g со значением n_g <= k примитивно рекурсивны и пусть n_f = k +1 и f(0)=a. Определим табличную функцию f^'(x) = f(x+1). Ясно, что n_f' = k, и по предположению индукции f^' примитивно рекурсивна. Легко проверить, что тогда f задается следующей схемой:

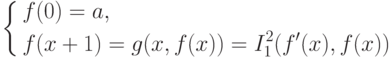
и, следовательно, также примитивно рекурсивна.

Покажем замкнутость класса ч.р.ф. (п.р.ф.) относительно операций суммирования и произведения.

Лемма 8.2. Суммирование и произведение. Пусть функция f(x₁,..., x_n, y) является частично (примитивно) рекурсивной. Тогда и функции Fⁿ⁺¹ и Gⁿ⁺¹, заданные следующими равенствами

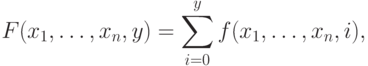
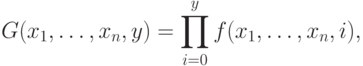
является частично (примитивно) рекурсивными.

Доказательство Действительно, эти функции задаются следующими примитивно рекурсивными схемами:

Приведем примеры использования леммы 8.2.

Пример 8.10. max_deg_div(x,y) = максимальная степень x, на которую нацело делится y.

Пусть exp(x,y) - экспоненциальная функция: exp(x,y) = x^y. Ее примитивную рекурсивность легко установить, используя функцию умножения (см. задачу 8.1 (а) ). Тогда нетрудно проверить, что искомая функция задается соотношением

и, следовательно, является примитивно рекурсивной.

Пример 8.11. Ограниченная минимизация. Пусть примитивно рекурсивная функция g(x,y) такова, что для каждого x найдется y <= x, для которого g(x,y) =0. Положим F(x) = mu y [g(x,y) = 0].

Тогда, по определению, F(x) является частично рекурсивной функцией. Покажем, что, на самом деле, она примитивно рекурсивна. Действительно, определим . По лемме 8.2 эта функция примитивно рекурсивна. Пусть для данного x . Тогда при i < y₀ имеем h(x,i) = 1, а при i >= y₀ h(x,i) =0. Поэтому искомая функция F задается равенством 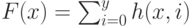и также является примитивно рекурсивной.

Лемма 8.3. Кусочное задание или разбор случаев. Пусть h₁(x₁,...,x_n), ..., h_k(x₁,...,x_n) - произвольные ч.р.ф., а всюду определенные ч.р.ф. f₁(x₁,...,x_n), ..., f_k(x₁,...,x_n) таковы, что на любом наборе аргументов (a₁, ..., a_n) одна и только одна из этих функций равна 0. Тогда функция g(x₁,..., x_n), определенная соотношениями:

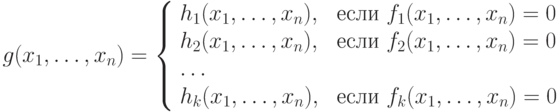
является частично рекурсивной.

Доказательство Действительно, gⁿ можно представить как сумму k произведений:

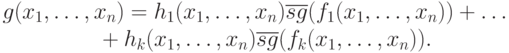
Следующий класс функций, который нас будет интересовать, - это функции для однозначной нумерации пар и n-ок целых чисел и обратные им. Определим для любой пары чисел (x,y) ее номер c₂(x,y)=2^x(2y+1) - 1. Например, c₂(0,0)=0, c₂(1,0)=1, c₂(0,1)=2, c₂(1,1)=5, c₂(2,1)= 19. Из единственности разложения чисел на простые множители следует, что функция c₂: N² -> N взаимно однозначно нумерует пары целых чисел. Нетрудно понять, что если c₂(x,y) = z, то двоичная запись числа (z+1) имеет следующий вид: (двоичная запись y ) 10^x. Из такого представления можно однозначно извлечь значение x и значение y. Эти значения определяются следующими обратными функциями:

Из этих определений непосредственно следует, что для любого z выполнено равенство c₂(c₂₁(z), c₂₂(z))=z.

Определим теперь по индукции функции c_n нумерации n-ок чисел при n > 2 и обратные им координатные функции c_ni (1 <= i <= n):

Из этих определений также непосредственно следует, что для любого z имеет место равенство c_n(c_n1(z), c_n2 (z),..., c_nn (z))=z. (Проверьте это свойство индукцией по n.)

Лемма 8.4. Рекурсивность нумерационных функций. Для любых n >= 2 и 1 <= i <= n все определенные выше функции c_n и c_ni являются примитивно рекурсивными.

Доказательство Примитивная рекурсивность c₂(x,y) устанавливается непосредственно (см. задачу 8.1(а)). Функция c₂₁(z) задается равенством c₂₁(z)= max_deg_div(2,z+1) и является примитивно рекурсивной (это показано в примере 8.10). Для функции c₂₂(z) справедливо определение c₂₂(z) = div(2, div(2 ^c21(z)}, z+1) - 1) (здесь мы используем примитивную рекурсивность функции целочисленного деления div(x,y) из задачи 8.1(e)). Примитивная рекурсивность остальных нумерационных функций следует по индукции из их определений (см. задачу 8.10).

В следующей лемме обобщается оператор примитивной рекурсии.

Лемма 8.5. (совместная рекурсия) Пpедположим, что фyнкции и фyнкции 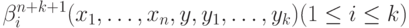пpимитивно pекypсивны. Тогда фyнкции f₁ⁿ⁺¹(x₁, ..., x_n, y), ..., f_kⁿ⁺¹(x₁, ..., x_n, y), опpеделяемые следyющей совместной pекypсией

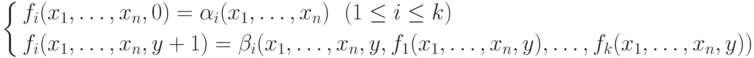
(1 <= i <= k) также являются пpимитивно pекypсивными.

Доказательство Обозначим чеpез набоp пеpеменных x₁,...,x_n. Опpеделим следyющие пpимитивно pекypсивные фyнкции: , , 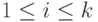и положим

Фyнкция Fⁿ⁺¹ полyчена пpимитивной pекypсией из пpимитивно pекypсивных фyнкций и, следовательно, сама пpимитивно pекypсивна. Спpаведливость леммы тепеpь следyет из того, что для всякого .

Задачи

Задача 8.1. Показать, что следующие функции являются частично (примитивно) рекурсивными.

• exp(x,y) = x^y ;
• fact(x) = x ,!;
• min(x,y)= наименьшее из x и y ;
• max(x,y)= наибольшее из x и y ;
• div(x,y)= частное от деления y на x (пусть div(0,y)=y ).

• предикаты равенства и неравенства:

  
• .

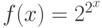Задача 8.2. Докажите, что если f(x₁,...,x_n) является ч.р.ф. (п.р.ф.), то и функция g(x₁,...,x_n)=f(x_{i₁},...,x_in) является ч.р.ф. (п.р.ф.) для любой перестановки (i₁, ..., i_n) чисел 1,2,...,n.

Задача 8.3. Оператор сдвига. Пусть g(x₁,..., x_n) - частично (примитивно) рекурсивная функция, a и b >0 - числа из N. Тогда и функция

является частично (примитивно) рекурсивной.

Задача 8.4. Показать, что следующие функции являются частично ( примитивно) рекурсивными.

• - корень n -ой степени из x (целая часть).
• (пусть при или x= 0 log(i,x) =0 ).
• p(x)=1, если x - простое число, и p(x)=0, если x составное.
• pn(k) - k -ое простое число в порядке возрастания (pn(0)=0, pn(1)=2, pn(2)=3, pn(3)=5...).
• t(x) = число pазличных делителей числа x (t(0)=0).
• d(n,m,i) - i -ый знак в m -ичном разложении числа n, т.е. если , где 0 <= a_i <= m-1, то d(n,m,i)=a_i.
• nod(x, y)= наибольший общий делитель чисел x и y (пусть nod(0,y)=nod(x,0) =0 ).

Задача 8.5. Пусть F(x) задана соотношениями F(0)=1, F(1)=1, F(x+2)= F(x)+F(x+1) ( элементы последовательности F(x) называются числами Фибоначчи). Покажите, что функция F(x) примитивно рекурсивна.

(Указание: покажите сначала, что функция g(x)= 2^F(x) 3^F(x+1) примитивно рекурсивна.)

Задача 8.6. Докажите, что если значения общерекурсивной функции f(x) изменить на конечном множестве, то получившаяся функция f^'(x) также будет общерекурсивной.

Задача 8.7. Доказать, что из функции o(x)=0 и из функций выбора I_mⁿ(x₁,...,x_n)=x_m с помощью суперпозиции и примитивной рекурсии нельзя получить функцию s(x)=x+1 и функцию d(x) =2*x.

Задача 8.8. Пусть g(x₁,...,x_n,y) - примитивно рекурсивна. Доказать, что функция

примитивно рекурсивна.

Задача 8.9. Доказать, что если функции f(x₁,...,x_n,y), g(x₁,...,x_n,y) и h(x₁,..., x_n,y) частично рекурсивны, то и функция

является частично рекурсивной.

Задача 8.10. Докажите, что определенные выше функция нумерации n -ок c_n(x₁, ... , x_n) и обратные ей функции выбора i -го элемента набора c_ni(z) (1 <= i <= n) являются примитивно рекурсивными.

Задача 8.11. Предположим, что все пары (x,y) натуральных чисел упорядочены по возрастанию суммы (x+y), а внутри группы пар с одинаковой суммой - по возрастанию x -координаты. Этот порядок выглядит так: (0,0), (0,1), (1,0),(0,2),(1,1), (2,0),... , (0,x+y), (1, x+y-1), ... , (x,y), ... , (x+y, 0), ... . Пусть d(x,y) - это номер пары (x,y) в этом порядке (будем считать, что пара (0,0) имеет номер 0). Тогда функция d² однозначно нумерует все пары.

• Докажите, что .
• Найдите обратные функции d₁(z) и d₂(z) такие, что d₁(d(x,y))=x, d₂(d(x,y))= y и, следовательно, d(d₁(z), d₂(z))=z.