НОУ ИНТУИТ | Введение в правовую информатику. Лекция 2: Теоретические основы правовой информатики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2009 | Уровень: для всех | Доступ: платный | ВУЗ: Кабардино-Балкарский государственный университет

|

Вам нравится? Нравится 62 студентам

| Поделиться |

Поддержать программу

Основное функциональное соотношение между энтропией и информацией имеет вид:

Из этой формулы следуют важные выводы:

увеличение меры Шеннона свидетельствует об уменьшения энтропии системы;
уменьшение меры Шеннона свидетельствует об увеличении энтропии системы.

Утверждение – основная единица, неделимая с точки зрения отражения смысла информации (семантики).

Высказывание – некоторое повествовательное утверждение, про которое можно однозначно сказать, истинно оно или ложно.

Эти два значения всевозможных высказываний обозначаются "истина" и "ложь" , "true" и "fаlse" или "1" и "0" .

Переменная, значениями которой могут быть лишь значения "1" или "0" называется логической переменной или булевой переменной.

Предикат – выражение, формула с логическими переменными, имеющая смысл при любых допустимых значениях этих переменных.

Логической (булевой) функцией называется некоторая функциональная зависимость 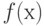f(х) , в которой аргумент – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f)={1,0} .

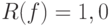Множество логических переменных $х,y\in Х$ с определенными над ним операциями:

$\overline{x}$ – отрицания или инверсии,
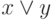$x\vee y$ – логического сложения или дизъюнкции,
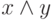$x\wedge y$ – логического умножения или конъюнкции

называется алгеброй предикатов и высказываний, если эти операции удовлетворяют следующим аксиомам:

Аксиома двойного отрицания: $\overline{\overline{x}}=x$ .
Аксиомы ассоциативности: $x\wedge y = y\wedge x$ , $x\vee y = y\vee x$ .
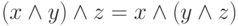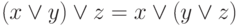Аксиомы переместительности: $(x\wedge y) \wedge z= x\wedge (y\wedge z)$ , $(x\vee y) \vee z= x\vee (y\vee z)$ .
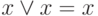Аксиомы одинаковых операндов: $x\wedge x = x$ , $x\vee x = x$ .
Аксиомы поглощения: $x\wedge (x \vee y)= x$ , $x\vee (x \wedge y)= x$ .
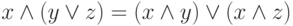Аксиомы распределения: $x \wedge(y\vee z)=(x\wedge y)\vee(x\wedge z)$ , $x \vee(y\wedge z)=(x\vee y)\wedge(x\vee z)$ .
Аксиомы де Моргана: $\overline{x \wedge y}=\overline{x} \vee \overline{y}$ , $\overline{x \vee y}=\overline{x} \wedge \overline{y}$ .
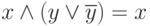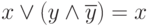Аксиомы нейтральности: $x \wedge(y \vee \overline{y})= x$ , $x \vee(y \wedge \overline{y})= x$ .
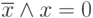Аксиома существования единицы (истина, true, 1) и нуля (ложь, false, 0), причем: $\overline{0}= 1$ , $\overline{1}= 0$ , $\overline{x} \vee x = 1$ , $\overline{x} \wedge x = 0$ .

Из этих аксиом следует ряд полезных соотношений, например,

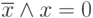$\overline{x} \wedge 1 = x$ , $\overline{x} \vee 0 = x$ , $\overline{x} \vee 1 = 1$ , $\overline{x} \wedge 0 = 0$ , $\overline{x} \vee x = 1$ , $\overline{x} \wedge x = 0$ .

Три базовые операции определяются таблицей их значений вида:

		$\overline{x}$	$x \wedge y$	$x \vee y$

Такая таблица всех значений некоторой логической функции называется таблицей истинности этой функции.

Кроме указанных трех базовых операций можно с их помощью ввести еще следующие важные операции алгебры предикатов:

импликации: $(x\Rightarrow y) \equiv (\overline{x} \vee y)$ ;
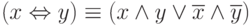эквиваленции: $(x\Leftrightarrow y) \equiv (x \wedge y \vee \overline{x} \wedge \overline{y})$ .

Операции импликации и эквиваленции имеют важное значение в правовой сфере, при решении задач, связанных с умозаключениями, выводами.

Всегда истинные формулы называют тавтологиями.

Логические функции эквивалентны, если совпадают их таблицы истинности, то есть совпадают области определения и значения, а также сами значения функции при одних и тех же наборах переменных.

Задача упрощения логического выражения состоит в преобразовании его к более простому (по числу переменных, операций или операндов) эквивалентному выражению.

Задача доказательства равенства двух логических выражений (функций) состоит в установлении эквивалентности этих функций.

Информационно–логическая (инфологическая) задача – это задача, в которой необходимо установить некоторые информационные или логические связи и сделать необходимые причинно-следственные логические выводы и заключения.

Рассмотрим пример формализации и решения правовой информационно–логической задачи.

Пусть Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. В ходе следствия Браун сказал, что преступники были на синем "Бьюике", Джонс сказал, что это был черный "Крайслер", Смит утверждал, что это был "Форд", но не синий. Каждый указал неправильно либо марку, либо цвет автомобиля. Определим истинный цвет и истинную марку автомобиля.

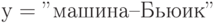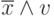Рассмотрим простые высказывания вида: х = "машина – синяя" , у = "машина – Бьюик" , z = "машина – черная" , u = "машина – Крайслер" , v = "машина – Форд" . На их основе, высказывание Брауна можно записать в виде сложного логического выражения вида $x \wedge y$ , высказывание Джонса – в виде $z \wedge u$ , а высказывание Смита – в виде $\overline{x} \wedge v$ . 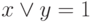Так как в каждом из этих выражений одна из переменных принимает значение "истина", то истинны и дизъюнкции вида: $x \vee y=1$ , $z \vee u=1$ , $\overline{x} \vee v=1$ . По определению конъюнкции, $(x \vee y)\wedge(z \vee u)\wedge(\overline{x} \vee v)=1$ . Упростим это выражение:

$1=(x \vee y)\wedge(z \vee u)\wedge(\overline{x} \vee v)= (x\wedge z\vee y\wedge z\vee x\wedge u\vee y\wedge u)\wedge(\overline{x} \vee v)=x\wedge z \wedge\overline{x} \vee y\wedge z \wedge\overline{x} \vee x\wedge u \wedge\overline{x} \vee y\wedge u \wedge\overline{x} \vee x\wedge z \wedge v \vee y\wedge z \wedge v \vee x\wedge u \wedge v \vee y\wedge u \wedge v= 0 \vee y \wedge x \wedge\overline{x} \vee 0 \vee 0 \vee 0 \vee 0 \vee 0 = y\wedge z \wedge\overline{x}$

Мы использовали тот факт, что одновременно не могут быть истинными два высказывания относительно цвета или два высказывания относительно марки машины. Так как конъюнкция истинна только тогда, когда 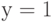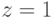у=1 , z=1 , $\overline{x}=1$ , то заключаем, что автомобиль был черным "Бьюиком".

Алгоритм – упорядоченная совокупность точных (формализованных) и полных команд исполнителю алгоритма, задающих порядок и содержание действий, которые он должен выполнить для нахождения решения любой задачи из рассматриваемого достаточно широкого класса однотипных задач.

Любая актуализация информации опирается на какие–то данные, любые данные могут быть каким–то образом актуализированы.

Данные – это некоторые сообщения, слова в некотором заданном алфавите.

Данные актуализируются, хранятся с помощью некоторых алгоритмов, процедур. В свою очередь, процедуры, алгоритмы существенно зависят от типа и структуры обрабатываемых ими данных.

Вопросы для самоконтроля

Каковы единицы измерения сообщений?
Как измеряется количество информации?
Что такое код, кодирование, декодирование? Привести примеры.
Что такое шифр, шифрование, дешифрование, ключ? Привести примеры.
В чем состоит принцип Кирхгоффа?
Какова формула Хартли?
Какова формула Шеннона?
Какова связь меры информации и хаоса в системе?
Что такое высказывание, предикат, логическая функция?
Каковы операции над предикатами?
Какие логические выражения эквивалентны?
Как упрощают предикаты?
Что такое алгоритм?
Что такое данные?

Задачи и упражнения

На одной странице судебного дела помещается 50 строк. В каждой строке книги содержится 70 символов кода ASCII. Сколько байт нужно для записи всего дела на диск, если в деле 128 полных страниц?
Правовая система может находиться в любом из 8 равновозможных состояний. Какое количество информации содержит сообщение о том или ином конкретном состоянии системы?
Составить таблицу истинности функции 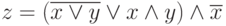$z=(\overline{x \vee y} \vee x \wedge y)\wedge \overline{x}$ . Упростить эту функцию и построить таблицу истинности для полученной после упрощения функции.

Дальше >>

Введение в правовую информатику

Введение в правовую информатику

Теоретические основы правовой информатики

Вопросы для самоконтроля

Задачи и упражнения

Вопросы и ответы

Студенты

Авторизоваться

Введение в правовую информатику

Введение в правовую информатику

Теоретические основы правовой информатики

Вопросы для самоконтроля

Задачи и упражнения

Вопросы и ответы

Студенты